Однофазные цепи переменного тока

 

Цель задания - приобретение навыков анализа и расчета цепей переменного тока.

Задание.

1. Определить токи во всех ветвях схемы и напряжение на каждом элементе цепи следующими методами:

а) проводимостей;

б) символическим методом эквивалентного преобразования схемы и узлового напряжения.

2. Составить баланс мощностей.

3. Построить векторную диаграмму токов и топографическую диаграмму напряжений.

Исходные данные приведены в табл. 2.1, схема - в прил. II.

 

Таблица 2.1

 

№ п/п	Е1, В	R1, Ом	R2, Ом	R3, Ом	С1, мкФ	C2, мкФ	C3, мкФ	L1, мГн	L2, мГн	L3, МГн
								12,75	38,2	12,75
					265,25		454,7	28,65	15,92	22,29
								9,55	19,1	25,5
							353,8	15,92	28,65	38,65
								12,75	38,2	15,92
							212,3	19,1	31,95	17,75
								9,55	63,9	12,75
							318,3	38,2	47,75	31,95
								19,1	25,5	38,2

Частота тока f = 50 Гц.

2.1. Пример расчета задания № 2

 

Находим величины реактивных сопротивлений:
X_L = wL = 2f 10^–3 = 314 L10^–3 Ом,

X_C = 1/wL = 1/(2C10^–6)= 10⁶/(314С) Ом,

где L - индуктивность, мГн, С - емкость, мкФ. Только в этих случаях допускается округление до целых чисел.

 

 

2.2. Расчет токов методом проводимостей

 

 

Находим величины реактивных сопротивлений в каждой ветви Х = Х_L – X_C, при Х(+) характер результирующего реактивного сопротивления индуктивный, при Х(-) - емкостный. В одной из ветвей возможен резонанс, когда Х_C = X_L, Х = 0. Составляем схему замещения. Рассмотрим пример (рис. 2.1).

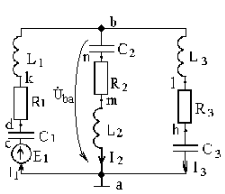
Рис. 2.1

 

Схема замещения имеет вид, показанный на рис. 2.2.

 

Z = R² +( X_L - X_C)²,

Z = R² + Х² .

 

Рис. 2.2

Находим активные и реактивные проводимости параллельных ветвей. Параллельная ветвь 2 (Х₂ - емкостный характер):

 

g₂ = R₂ / (R₂² + Х₂²); b₂ = - X₂ / (R₂² + Х₂²).

Параллельная ветвь 3 (Х₃ – индуктивный характер):

 

g₃ = R₃ / (R₃² + Х₃²); b₃ = Х₃ / (R₃² + X₃²).

В результате преобразования схема будет иметь вид (рис. 2.3).

Y₂ = g₂² + b₂²;

Y₃ = g₃² + b₃².

 

 

 

Рис. 2.3

 

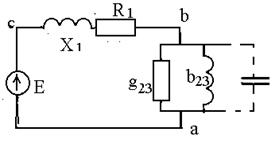
Определяем эквивалентные проводимости двух ветвей:

 

 

 

g₂₃ = g₂ + g₃ ,

b₂₃ = b₃ – b₂ ,

Y₂₃ = 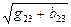= Y_ab .

 

Рис. 2.4

 

Характер проводимости b₂₃ определяется по знаку b₂₃: при (+) - индуктивный, при (–) - емкостный. Схема имеет вид, показанный на рис. 2.4.

На участке ab от проводимостей переходим к сопротивлениям, т.к. этот участок соединен последовательно с участком bс:

 

R_ab = g₂₃ /Y₂₃², X_ab = b₂₃ /Y₂₃².

 

При переходе к сопротивлениям схема замещения представлена на рис. 2.5, а.

 

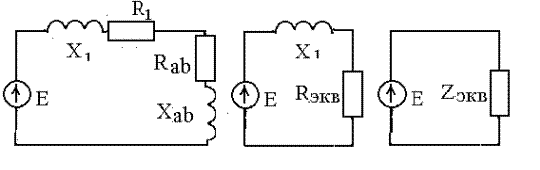
а б в

Рис. 2.5

 

Определяем эквивалентное сопротивление схемы рис. 2.5, б и 2.5, в:

 

R_экв = R₁ + R_ab; X_экв = X₁ + X_ab; ;

j_экв = arctg (X_экв / R_экв).

 

Вычисляем ток I₁ первой ветви и источника по закону Ома.

 

I₁ = E / Z_экв, I_1a=I₁cosj_экв, I_1P=I₁sinj_экв.

 

Определяем напряжение на параллельном участке ab:

 

U_ab,aк = I₁R_ab; U_ab,p = I₁X_ab; = ,

 

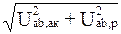где I_aк – активная составляющая тока; I_p – реактивная составляющая тока.

Вычисляем токи и углы сдвига фаз между токами и напряжениями в параллельных ветвях:

 

I­₂ = Y₂U_ab; I_2aк = g₂U_ab; I_2р = b₂U_ab; I₂ = ;

;

I₃ = Y₃U_ab; I_3aк = g₃U_ab; I_3р = b₃U_ab; I₃ = ; .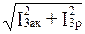

 

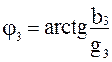Проверка: I_1a = I_2a + I_3a; I_1р = I_2р + I_3р.

 

Значения модулей токов I₁; I₂; I₃ должны быть равны соответствующим значениям, полученным другими методами.

 

 

2.3. Символический метод расчета цепей синусоидального тока

 

 

Представляем полные комплексные сопротивления каждой ветви в алгебраической и показательной форме.

 

Z = R + j(X_L - X_C) =Ze^±jj,

где модуль сопротивления Z = R² + X² ; j = arctg (X / R).

Знак (+) соответствует индуктивному сопротивлению, а знак (-) - емкостному.

Обратные преобразования Ze^±jj =  Zcosj  jZsinj.

При каждом преобразовании обязательно представлять вектор на комплексной плоскости. Отсчет показателя степени угла  производится против часовой стрелки, если  – положительный; по часовой, если  – отрицательный.

Z = Z ₂ Z ₃ / (Z ₂ + Z ₃).

 

Эквивалентное сопротивление цепи при смешанном соединении (рис. 2.6, 2.7):

Z _экв = Z ₁ + Z_{а b}.

 

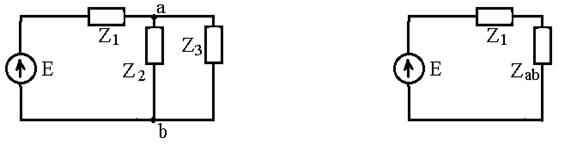
Рис. 2.6 Рис. 2.7

 

Определяем токи в ветвях

 

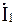= / Z _экв = I₁e ^{± jj} = I_1a  jI_1р;

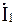= Z ₃ / (Z ₂ + Z ₃) = I₂e ^{± jj} = I_2a  jI_2р;

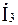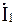= Z ₂ / (Z ₂ + Z ₃) = I₃e ^{± jj} = I_3a  jI_3р.

 

Найденные значения токов должны быть представлены в алгебраической и показательной формах.

Проверяем правильность вычислений по первому закону Кирхгофа:

 

= + .

 

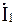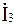Находим напряжение на параллельном участке = 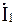Z _ab,
= Z ₂ или = 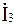Z ₃. Напряжение должно соответствовать ,найденному методом проводимостей.

 

 

2.4. Расчет методом узловых потенциалов

 

 

Определяем комплексные проводимости ветвей с точностью до четвертой значащей цифры (для схемы рис. 2.8).

 

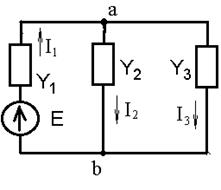
Y ₁ = 1 / (Z₁e ^±jj1 ) =

= Y₁e ^±jj1 =  g₁  jb₁,

Y ₂ = 1 / (Z ₂e ^±jj2 ) =

= Y₂e ^{± jj2} =  g₂  jb₂,

Y ₃ = 1 / (Z₃e ^{± jj 3} ) =

= Y₃e ^{± jj3} =  g₃  jb₃.

 

 

Рис. 2.8

 

Выбираем направление токов I₁; I₂; I₃.

Определяем напряжение U_ab:
;

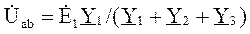определяем токи в ветвях:

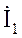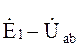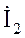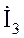= () / Z ₁; = / Z ₂; = / Z ₃ .

Выполняем проверку по первому закону Кирхгофа.

 

 

2.5. Баланс мощностей

 

 

Баланс мощностей .

Мощность источника 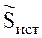= = 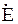P_ист  jQ_ист,

где - сопряженный комплекс тока (знак перед (j) меняется на противоположный).

 

P_пр = I₁²R₁ + I₂²R₂ + I₃²R₃; Q_пр =  I₁²X₁  I₂ ²X₂  I₃²X₃,

где I₁, I₂, I₃ - модули комплексов токов.

 

P_ист = P_пр; Q_ист = Q_пр.

 

Погрешность вычислений не должна превышать 2 %.

 

2.6. Построение векторной диаграммы

 

 

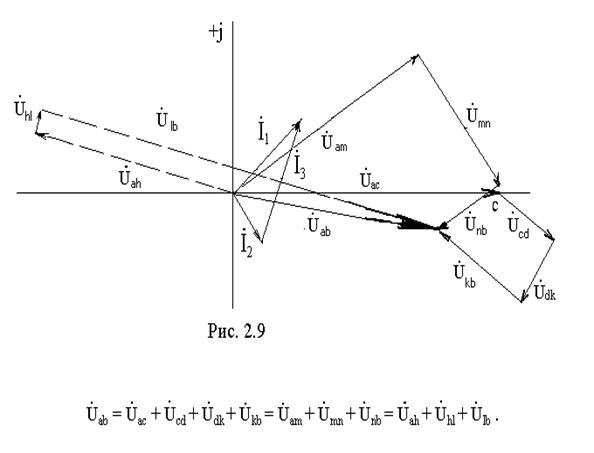
Находим напряжение на каждом элементе схемы и строим векторную диаграмму (для схемы рис. 2.1), представляющую собой графическое изображение первого и второго законов Кирхгофа на комплексной плоскости.

 

= X_C1e ; = R₁;

= X_L1e ^j90 ; 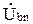= X_C2e ;

= R₂ ; 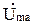= X_L2e ^j90 ;

= X_L3e ^j90; 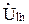= R₃ ;

= X_C3e .

Строим векторную диаграмму (рис. 2.9).

ВОПРОСЫК ЗАДАНИЮ № 2

Линейные цепи однофазного синусоидального тока. Элементы цепи переменного тока. Аналитический и символический методы расчета цепей переменного тока. Баланс мощностей в цепи переменного тока.

ЗАДАНИЕ № 3