Цилиндр (прямой круговой).
Вспомним формулы для вычисления поверхности цилиндра:
Боковая поверхность цилиндра: S 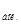 = 2 πRH.
= 2 πRH.
Полная поверхность цилиндра:
S 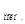 = 2S
= 2S 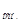 + S
+ S 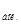 = 2π R
= 2π R 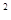 + 2 πR H= 2 πR(R + H).
+ 2 πR H= 2 πR(R + H).
1. (Устно.) Радиус основания цилиндра 2 м, высота 3 м.
Найти диагональ осевого сечения. (5 м)
2. (Устно.) Осевое сечение цилиндра – квадрат, площадь
которого Q. Найти площадь основания. (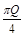 )
)
3. В цилиндре проведена параллельно оси плоскость, отсекающая
от окружности основания дугу в 120°. Длина оси h =10 см;
её расстояние от секущей плоскости а = 2 см.
Определить площадь сечения. (40 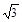 ≈ 70 см
≈ 70 см 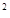 )
)
4. Площадь основания цилиндра относится к площади осевого
сечения, как π: 4. Найти угол между диагоналями осевого
сечения. (90°)
5. Диагональ осевого сечения равностороннего цилиндра
(в осевом сечении – квадрат) равна а. Найти объём правильной
вписанной в этот цилиндр восьмиугольной призмы. (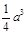 )
)
| Поверхность цилиндра | 6. Высота цилиндра на 10 см больше радиуса
основания, а полная поверхность равна 144 л см 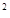 . .
|
Определить радиус основания и высоту. (4 см и 14 см)
7. Цилиндрическая дымовая труба с диаметром в 65 см имеет
высоту 18 м. Сколько квадратных метров жести нужно
для её изготовления, если на заклёпку уходит 10%
всего требующегося количества жести? (Около 40 м 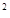 )
)
8. Полуцилиндрический свод подвала имеет 6 м длины и 5,8 м
в диаметре. Определить полную поверхность подвала. (≈ 116м 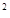 )
)
Конус (прямой круговой).
Формулы для вычисления поверхности конуса:
Боковая поверхность конуса: S 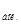 = πRL.
= πRL.
Полная поверхность конуса:
S 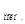 = S
= S 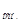 + S
+ S 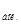 = πR
= πR 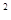 + πRL = πR(R + L).
+ πRL = πR(R + L).
1. (Устно.) Радиус основания конуса 3 м, высота 4 м.
Найти образующую. (5 м)
2. (Устно.) Образующая конуса l наклонена к плоскости основания
|
|
под углом в 30°. Найти высоту. ( )
)
3. Отношение площади основания конуса к площади осевого
сечения равно π. Найти угол наклона образующей к основанию. (45°)
4. Высота конуса 20, радиус его основания 25. Найти площадь
сечения, проведённого через вершину, если его расстояние
от центра основания конуса равно 12. (500)
5. Образующая конуса 13 см, высота 12 см. Конус этот пересечён
прямой МN, параллельной основанию; расстояние её от
основания равно 6 см, а от высоты 2 см. Найти отрезок этой
прямой, заключённый внутри конуса. (3 см)
| Поверхность конуса | 6. (Устно.) Высота конуса H = 6, радиус основания r = 8. Найти боковую поверхность. (80 π) |
7. (Устно.) Высота конуса h = 4, образующая l = 5.
Найти полную поверхность. (24 π)
8. Определить величину поверхности, полученной вращением
хорды около диаметра, выходящего из её конца, если диаметр
равен 25 см, а хорда равна 20 см. (240 π см 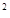 )
)
9. Из точки А на окружности радиуса r = 7 м проведена
касательная АВ = l =24 м, а из её конца В – секущая ВОС
через центр. Определить величину поверхности, которую
описывает отрезок ВС секущей, вращаясь вокруг касательной. (286,72 π м 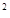 )
)
| Развёртка конуса | 10. Высота конуса 4, радиус основания 3; боковая поверхность конуса развёрнута на плоскость. Найти угол полученного сектора. (216°) |
Усечённый конус.
Поверхность усечённого конуса вычисляется
по формуле:  .
.
1. (Устно.) Радиусы оснований усечённого конуса 3 м и 6 м,
высота 4 м. Найти образующую. (5 м)
2. Радиусы оснований усечённого конуса 11 см и 16 см;
образующая 13 см. Найти расстояние от центра меньшего
|
|
основания до окружности большего. (20 см)
3. Образующая усечённого конуса равна 2 а и наклонена
к основанию под углом 60°. Радиус одного основания вдвое
больше радиуса другого основания. Найти каждый из радиусов. (а и 2 а)
4. Радиусы основания усечённого конуса 3 дм и 7 дм; образующая
5 дм. Найти площадь осевого сечения. (30 дм 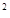 )
)
5. Площади оснований усечённого конуса 4 м 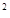 и 16 м
и 16 м 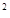 .
.
Через середину высоты проведена плоскость параллельно
основанию. Найти площадь сечения. (9 м 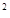 )
)
6. Определить высоту усечённого конуса, если его полная
поверхность равна 572π м 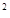 , а радиусы оснований 6 м и 14 м. (15 м)
, а радиусы оснований 6 м и 14 м. (15 м)
7. В усечённом конусе высота H = 63 дм, образующая
l = 65 дм и боковая поверхность S =26π м 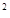 .
.
Определить радиусы оснований. (28 дм и 12 дм)
8. В усечённом конусе образующая l =5 см, а радиусы оснований
1 см и 5 см. Найти радиус цилиндра с такой же высотой и такой
же величиной боковой поверхности. (5 см)
Объём цилиндра.
Объём цилиндра находим по формуле: V = πR 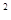 H.
H.
1. Боковая поверхность цилиндра равна S, а длина окружности
основания С. Найти объём. (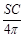 )
)
2. Боковая поверхность цилиндра развёртывается в квадрат
со стороной а. Найти объём. (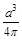 )
)
3. Высота цилиндра равна H, и в развёртке его боковой
поверхности образующая составляет с диагональю угол 60°.
Определить объём. (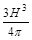 )
)
4. Определить объём цилиндра, вписанного в правильную
шестиугольную призму, у которой каждое ребро равно а.
Объём конуса.
Формула объёма конуса: V = 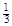 πR
πR 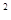 H.
H.
1. Осевым сечением конуса служит равнобедренный
прямоугольный треугольник; площадь его 9 м 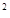 .
.
Найти объём конуса. (9π м 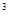 )
)
|
|
2. Площадь основания конуса 9 π см 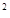 , полная поверхность
, полная поверхность
его 24 π см 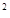 . Найти объём конуса. (12π см
. Найти объём конуса. (12π см 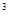 )
)
3. Высота конуса равна 15 м, а объём равен 320π м 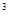 .
.
Опредёлить полную поверхность. (200π см 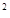 )
)
4. Высота конуса равна 6 см, а боковая поверхность 24π см 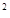 .
.
Определить объём конуса. (24π см 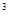 )
)