Предприятие может выпустить три вида продукции: П1, П2, П3. Для выпуска продукции требуются ресурсы трех видов: трудовые, станочное оборудование и полуфабрикаты. Объемы и нормы расхода ресурсов приведены в условных величинах в Таблице 2, цифровые значения – в Таблице 3.
Таблица 1 – Объемы и нормы расхода ресурсов, условные величины.
| Наименование ресурса | Вид продукции | Объем ресурса | ||
| П1 | П2 | П3 | ||
| Расход ресурса на единицу продукции | ||||
| Трудовые ресурсы, чел-ч | а1 | а2 | а3 | a |
| Станочное оборудование, станкосмены | b1 | b2 | b3 | b |
| Полуфабрикаты, кг | c1 | c2 | c3 | c |
| Прибыль с единицы продукции, руб | p1 | p2 | p3 | max |
| Выпуск, шт | x1 | x2 | x3 |
Таблица 2 - Объемы и нормы расхода ресурсов, цифровые значения.
| № вар. | а1 | а2 | а3 | a | b1 | b2 | b3 | b | c1 | c2 | c3 | c | p1 | p2 | p3 |
Требуется найти, сколько и какого вида продукции необходимо выпускать, чтобы план был оптимальным по критерию прибыли, т.е. таким, при котором получаемая прибыль была бы максимальной
Решение:
Общей задачей линейного программирования – определение максимального(минимального) значения функции

При условиях



где cj, xj, aij – заданные постоянные величины,  .
.
Функция F называется целевой функцией задачи, а условия – ограничениями задачи. Совокупность чисел, удовлетворяющих ограничениям задачи, называется допустимым решением. Решение, при котором целевая функция задачи принимает максимальное (минимальное) значение, называется оптимальным.
Таблица 3 – Исходные данные для расчета по варианту № 20.
| Наименование ресурса | Вид продукции | Объем ресурса | ||
| П1 | П2 | П3 | ||
| Расход ресурса на единицу продукции | ||||
| Трудовые ресурсы, чел-ч | ||||
| Станочное оборудование, станкосмены | ||||
| Полуфабрикаты, кг | ||||
| Прибыль с единицы продукции, руб | max | |||
| Выпуск, шт | x1 | x2 | x3 |
Схема решения задач линейного программирования в MS Excel 2010 следующая:
1. Составить математическую модель.
2. Ввести на рабочий лист Excel условия задачи:
а) создать форму на рабочем листе для ввода условий задачи;
б) ввести исходные данные, целевую функцию, ограничения и граничные условия.
3.Указать параметры в диалоговом окне Поиск решения.
4. Проанализировать полученные результаты.
Целевая функция задачи: 
Ограничения: 4 

6 



На листе создадим форму для заполнения данных, с выделенными ячейками, которые необходимо будет заполнять
В ячейки В3:D3 выдается ответ значений хj. В ячейке G5 – с использованием функции СУММПРОИЗ, записываем целевую функцию же образом в ячейки F. Таким же образом в ячейки D8:D10 вводим значение, левой части ограничений (Рисунок 1)
Следуя Данные→Анализ выбираем Поиск решения. В диалоговом окне в Параметрах поиска решения выбираем следующее:
· в поле Оптимизировать целевую функцию выбираем ячейку со значением целевой функции – G5;

Рисунок 1 – Расчетная таблица для варианта 20
· выбираем, максимизировать целевую функцию;
· в поле Изменяя ячейки переменных выбираем ячейки со значениями искомых переменных B3:C3 (пока в них нули или пусто);
· в области В соответствии с ограничениями с помощью кнопки Добавить размещаем все ограничения нашей задачи;
· в поле Выберите метод решения указываем Поиск решения линейных задач симплекс-методом;
· нажимаем кнопку Найти решение.
В диалоговом окне выбираем Добавить, добавляем все шесть ограничений. В поле Ограничение выделяем диапазон F10:F11 и нажимаем кнопку Добавить. Выбираем OK. После нажатия кнопки Поиск решения возможно выбрать три результата:
1. Отчет по устойчивости (Рисунок 3,4) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных.
2. Отчет по результатам (Рисунок 5,6) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй – значения искомых переменных, полученные в результате решения задачи, в третьей – результаты оптимального решения для ограничений.
3. Отчет по пределам (Рисунок 7,8) содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи.
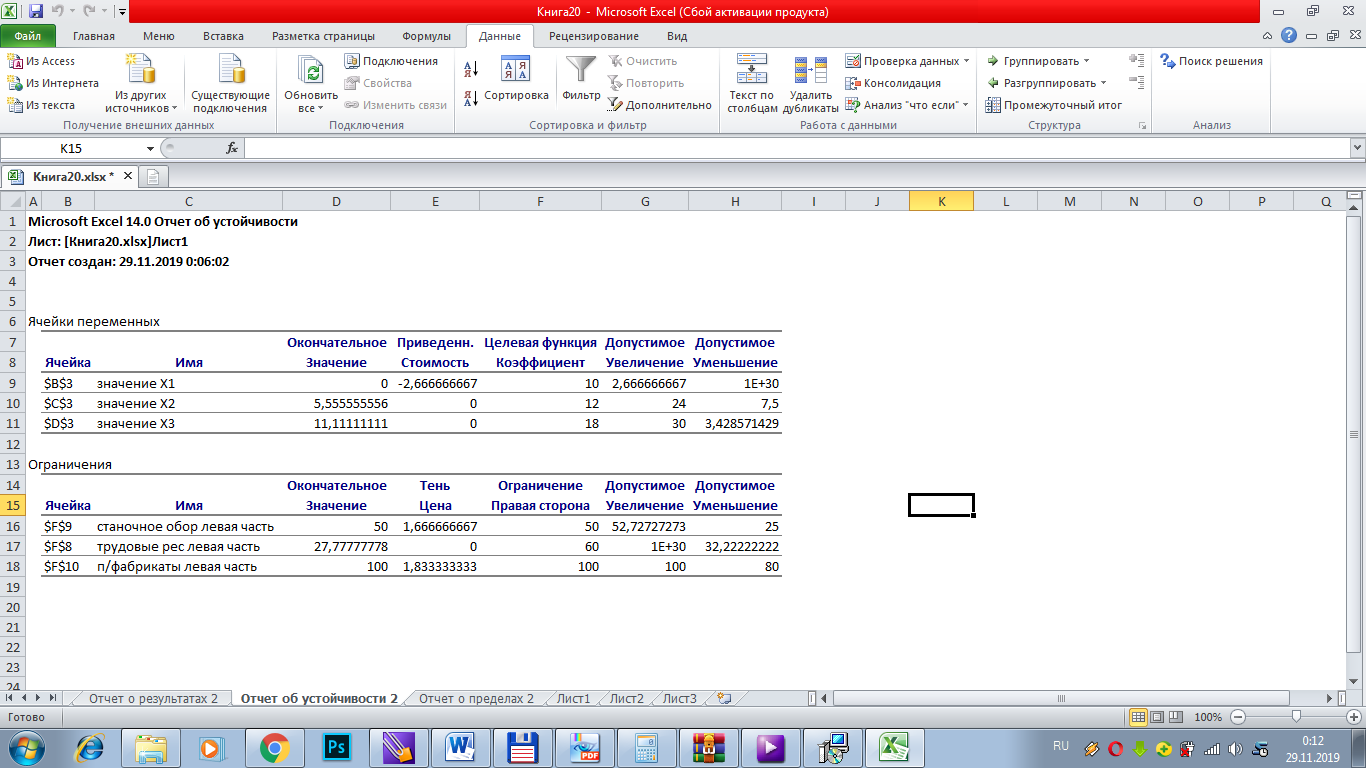
Рисунок 2 – Отчет об устойчивости

Рисунок 6 – Отчет о результатах

Рисунок 3 – Отчет о пределах
Литература
Решение задач линейного программирования в Microsoft Excel 2010: методические указания к выполнению лабораторных работ по информатике для обучающихся по всем программам бакалавриата и специалитета дневной формы обучения / сост. Н. Д. Берман, Н. И. Шадрина. – Хабаровск: Изд-во Тихоокеан. гос. ун-та, 2015. – 27 с.