Математическая модель двухфазной фильтрации

ТЕОРИЯ ДВУХФАЗНОЙ ФИЛЬТРАЦИИ НЕСМЕШИВАЮЩИХСЯ ЖИДКОСТЕЙ

В связи с проектированием и анализом разработки нефтяных и газо­вых месторождений приходится исследовать совместное течение в по­ристой среде нескольких жидкостей, чаще всего воды, нефти и газа, представляющих собой обособленные фазы, не смешивающиеся между собой.

Рассмотрим здесь наиболее простое двухфазное течение, соответст­вующее вытеснению нефти, первоначально заполнявшей поры, водой или газом. Этот процесс является основным, как при естественном водонапорном режиме (при вторжении в пласт краевой воды или газа газовой шапки, продвигающих нефть к забоям добывающих скважин), так и при, так называемых, вторичных методах добычи нефти - закачка вытесняющей жидкости или газа через систему нагнетательных скважин для поддержания давления в пласте и продвижения нефти к добывающим скважинам.

При фильтрации двух несмешивающихся жидкостей рассматривают понятие насыщенности порового пространства каждой фазой. Насы­щенность элемента пористой среды данной фазой определяется как относительная часть объема активных пор среды, занятая этой фазой:

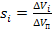(1)

где i принимает значения 1 и 2,

s₁, s₂ - насыщенность соответственно смачивающей и несмачивающей фазами;

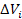-объем среды, занятой жидкостью;

-общий объем активных пор в данном элементе.

Очевидно, справедливо равенство

, (2)

поэтому из двух насыщенностей независима только одна, и обычно характеристики движения в потоке двухфазной жидкости представляются в функции от насыщенности первой (смачивающей) фазой и вводится обозначение .

При описании двухфазных течений обычно вместо фазовых проницаемостей вводят так называемые относительные проницаемости фаз, определимые из отношений

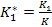, , (3)

где k₁, k₁ - фазовые проницаемости,

k – проницаемость при однофазной фильтрации.

В большинстве опытов показано, что для данной структуры порис­той среды относительные проницаемости являются в основном функциями насыщенности, а если и наблюдается влияние иных параметров (например, отношения коэффициентов вязкости фаз), то ими обычно пренебрегают.

Типичные экспериментальные кривые фазовых проницаемостей приведены на рис. 1 (кривая 1 относится к более смачивающей жидкости-воде, кривая 2 - к менее смачивающей - нефти; кривая 3 относится к случаю, когда первая фаза является газом; s- газонасыщен­ность).

Рис. 1. Кривые зависимости относительных фазовых проницаемостей от насыщенности

В гидродинамических расчетах часто удобно пользоваться эмпирическими зависимостями значений относительной фазовой проницаемости от насыщенности, полученными из экспериментальных данных. Рассмотрим эмпирические формулы, полученные Чень-Чжун-Сяном, которые можно применять при оценочных расчетах.

Для воды и нефти (s-водонасыщенность):

(6)

. (7)

Закон фильтрации записывается для каждой из фаз:

(3)

где w₁ и w₂ - скорости фильтрации фаз;

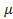₁ и ₂ -динамические коэффициенты вязкости жидкостей;

р₁ и р₂- функции давлений в соответствующих фазах,

ω- площадь, через которую определяется фильтрация.

В общем случае давления р₁ и р₂ в фазах не совпадают из-за действия поверхностного натяжения и связаны равенством

, (4)

здесь р_к -капиллярное давление, определяемой по формуле Лапласа

, (5)

где а - коэффициент поверхностного натяжения на границе раздела фаз,

R_{1 ,} R₂ –главные радиусы кривизны поверхности раздела фаз.

На практике капиллярное давление определяют по формуле

, (6)

где Θ – краевой угол смачивания,

J(s) – безразмерная функция (функция Леверетта), определяемая экспериментально для каждой породы-коллектора.

Уравнения неразрывности записываются для каждой фазы

. (7)

Математическая модель замыкается уравнениями состояния жидкостей и граничными условиями.