Математическая модель процесса вытеснения

 

Рассмотрим процесс вытеснения, происходящий в прямолинейном тонком горизонтальном образце (рис.2), представленном однородной и изотропной пористой средой, т. е. его пористость m и проницаемость k постоянны. Координата х отсчитывается вдоль образца, направление течения - горизонтальное. Поперечное сечение образца (площадь сечения обозначим ω) предположим достаточно малым, так что давление и насыщенность можно считать постоянными по сечениям. Давление р в водяной и нефтяной фазах считаем одинаковым в силу пренебре­жения капиллярным давлением, обе фазы несжимаемы, температура постоянна.

Рис. 2. Схема прямолинейно-параллель­ного вытеснения нефти водой

 

В рассматриваемый образец, первоначально заполненный нефтью, через сечение х=0 закачивается вода. В процессе вытеснения образуется зона совместного движения воды и нефти, характеризуемая водонасыщенностью s_в и нефтенасыщенностью s_н. Так как s_в +s_н =1 и обозначив

s_в= s, имеем s_н = 1- s_в= 1- s. (8)

Закон фильтрации Дарси каждой фазы можно представить в виде:

. (9)

Здесь w_в, w_н, Q_в, Q_н - скорости фильтрации и объемные расходы соответственно воды и нефти;

μ_в, μ_н - коэффициенты динамической вязкости фаз;

k_в(s) и k_н(s) - относительные фазовые проницаемости;

s = s_в - водонасыщенность.

Так как пористость и плотности постоянны, то уравнения неразрывности (7) будут иметь вид

.

Или с учетом (8)

. (10)

Сложив уравнения неразрывности (10) для обеих фаз, по­лучим:

(11)

откуда найдем первый интеграл:

w_B + w_H = w(t) или Q_В + Q_Н = Q(t) (12)

Равенства (12) показывают, что суммарная скорость w двухфазного потока (а значит, и суммарный расход фаз Q(t) не зависит от координаты х, т.е. является либо постоянной вели­чиной, либо известной функцией времени.

Исключим градиент давления dp/dx, поделив почленно одно на другое уравнения (10):

, (13)

где введено обозначение .

Применив к (13) правило производных пропорций и использовав (11), получим

.

Обозначив

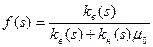(14)

из предыдущего равенства найдем: w_B=f(s)w(t) и w_B=[1-f(s)]w(t) (15)

Введенная здесь функция насыщенности f(s), называемая функцией распределения потоков фаз или функцией Бакли-Леверетта.

Типичные графики f(s) и ее производной f'(s) приведены на рис.3. Подставив теперь равенство (15) для w_B в уравнение (10), получим

. (16)

Поскольку насыщенность есть функция двух переменных s = s(x,t), то применяя правило дифференцирования сложной функции получим

.

Рис.3 Приведем окончательно уравнение (16) к виду

, (17)

которое является дифференциальным уравнением только относительно насыщенности. Изменение насыщенности во времени по пласту можно получить в результате решения уравнения (17) независимо от распределения давления p(x.t). Это уравнение известно в литературе как уравнение Бакли - Леверетта по имени авторов, впервые его полу­чивших.

Для нахождения распределения насыщенности к уравнению (17) нужно добавить начальное и граничное условия:

при t = 0 s(x,0) = φ(x), x>0;

при х = 0 s(0,t) = ψ(t), t> 0. (18)

Первое из условий (18) означает, что в момент времени t = 0 (до начала процесса вытеснения) в пласте имеется некоторое известное распределение насыщенности s вытесняющей фазы, определяемое функ­цией φ (х). Согласно второму условию (18), при t>0 в пласт через нагнетательную галерею, расположенную на «линии» х = 0, закачи­вается вытесняющая жидкость (вода), насыщенность которой при х = 0 меняется со временем по заданному закону ψ (t). В некоторых случаях можно считать, что

φ (х) = s₀ = const при t = 0,

ψ(t)= s₀= const при х = 0. (19)

Это-случай кусочно-постоянных начальных данных, имеющий важ­ное значение для практических приложений. Величина начальной водо-насыщенности s₀ влияет на процесс заводнения и определяет структуру зоны вытеснения.

В дальнейшем для простоты будем считать суммарную скорость фильтрации w(t) (а значит, и суммарный расход Q) постоянной ве­личиной:

w(t) = w = const; Q(t) = Q =const.

В процессе поступления воды в пласт ее насыщенность будет меняться со временем вдоль направления движения х, т.е. s = s(x.t). Тогда дифференциал функции двух переменных будет равен

(19)

Линии, на которых насыщенность постоянна, называются изосатами. Уравнение изосаты s(x.t)=const, тогда ds=0 или в дифференциальном виде

. (20)

Уравнение (17) и (20) образуют систему однородных линейных уравнений относительно ds/dt и ds/dx, которая имеет нетривиальное (отличное от нуля) решение, если определитель равен нулю

=0,

откуда находим:

. (21)

Так как правая часть уравнения (21) постоянна, то решение будет иметь вид:

(22)

где х₀ – значение координаты с начальной водонасыщенностью s₀ при t = 0. Уравнение (22) задает положение точки с заданной насыщенностью в любой момент времени. Однако функция не является монотонной, имеет максимум (см. рис.3). Это означает в соответствии с (21), что на движущейся кривой s(x) некоторые промежуточные значения насыщенности будут перемещаться быстрее, чем значения насыщенности большие или меньшие. И спустя определенный про­межуток времени после начала вытеснения форма профиля насыщен­ности будет иметь вид, подобный графику f'(s) на рис.4. Из рисунка видно, что для любого значения х насыщенность становится неод­нозначной (имеет три различных значения). Такое положение физически невозможно и, следовательно, начиная с этого момента времени, не­возможно непосредственное применение уравнения (22).

Введение скачка (или фронта) насыщенности (прямая АВ на рис.4) позволяет устранить многозначность решения. Поло­жение скачка насыщенности определяется из условия материального баланса на скачке, так что площади сегментов, заштрихованные на рис. 4, равны.

 

Рис. 4. Схематичный профиль Рис.5. Схема фронта (скачка)

насыщенности насыщенности

 

Заметим, что в действительности введенный математический скачок насыщенности не имеет места, а возникает вследствие пренебрежения капиллярными силами. На самом деле существует некоторая конечная зона длиной δ (см. рис. 4), в которой насыщенность резко падает от значения s_с до s_* (вдоль кривой АВ₁). Размеры этой зоны зависят от капиллярного давления и обычно малы по сравнению с возрастающей со временем зоной смеси х_с в пределах всего разрабатываемого пласта.

Несмотря на то, что дифференциальные уравнения (10), выражающие баланс массы каждой фазы, в точках введенного разрыва не имеют смысла, сам баланс, естест­венно, должен выполняться.

Рассмотрим условия сохра­нения массы каждой из фаз при прохождении разрыва через некоторый элемент объема пористой среды (рис.5), ограниченный двумя по­верхностями ∑⁺ и ∑^- по обе стороны от разрыва насыщенности (фронт).

Пусть в некоторый момент времени t фронт имел координату х_с, а через малый промежуток времени Δt переместился в положение х_с + Δх_с. При этом в элемент пласта длиной Δx войдет слева объем воды, равный w_B⁺ ω Δt, а выйдет объем w_B^- ω Δt, т.е. объем воды уве­личится на (w_B⁺- w_B^-)ωΔt, где ω -площадь поперечного сечения пласта. Вследствие этого насыщенность увеличится от значения s^- до s⁺ т.е. объем воды возрастет на величину

(s⁺ - s^-)m ω Δх_с.

Тогда закон сохранения массы воды (в предположении, что она несжимаема) дает:

(w_B⁺- w_B^-)ωΔt=(s⁺ - s^-)m ω Δх_с

откуда следует

(23)

где знаки «-» и «+ » соответствуют условиям непосредственно перед и после разрыва.

Уравнение сохранения массы для нефти приводит к аналогичному (23) равенству, поскольку суммарная скорость фильтрации (см. (12)) сохраняется:

. (24)

Перейдя в (23) к пределу при Δx→0 и Δt→0 и использовав равенство (15), получим:

. (25)

Здесь и далее индексом «с» обозначены величины, относящиеся к фронту (скачку) насыщенности. Выражение (25) задает скорость v_c распространения фронта насыщенности и известно как условие на скачке.

Если насыщенности по обе стороны фронта постоянны (в нашем случае s^- = s₀, s ⁺ = s_c, скачок насыщенности Δs = s+- s^- = const), то уравнение (25) можно проинтегрировать и найти положение фронта как функцию времени:

. (26)

где х_С0- положение скачка при t = 0 (в нашем случае при постоянном начальном распределении насыщенности х_С0 = 0).

Для фронтальной насыщенности s_с, как и для любого значения s, выполняется равенство (21)

. (27)

Кроме того, скорость скачка определяется равенством (25), в ко­тором s⁺ = s_c и s^- = s₀. Приравняв правые части (25) и (27), получим уравнение для определения фронтальной насыщенности s_с:

. (28)

Это уравнение имеет простую геометрическую интерпретацию (см. рис. 3а): оно представляет собой уравнение касательной, про­веденной из точки (s₀, f(s₀)) к кривой f(s), где s_c—абсцисса точки касания. Это дает простой графический способ определения фронтальной насыщенности по известной функции Бакли-Леверетта f(s).

Таким образом, мы имеем две группы выражений: уравнения (21) и (22), которые можно использовать для расчета скорости и коор­динаты данного значения насыщенности в области непрерывного профи­ля, и уравнения (25) и (26), при помощи которых можно найти скорость и положение скачка насыщенности.