Пособие для учащихся
Механика
Киров
УДК 531 (075.3)
ББК 22.33+74.202
С 17
Печатается по решению редакционно-издательского совета Лицея естественных наук г. Кирова
Пособие представляет собой сборник задач по всем темам школьного курса механики, в который включены вопросы и задачи различной степени сложности. Большинство задач заимствовано автором из известных сборников задач, из материалов ЕГЭ, а также из пособий для подготовки к вступительным экзаменам по физике в вузы. Часть задач являются авторскими. Пособие не заменяет программные задачники (авторы: А. П. Рымкевич, Г. Н. Степанова и другие), а дополняет их.
Пособие предназначено для работы на уроках и факультативных занятиях с учащимися Лицея естественных наук
Рецензент: К. А. Коханов, кандидат педагогических наук, доцент кафедры дидактики физики Вятского государственного гуманитарного университета, заместитель заведующего кафедрой дидактики физики.
С 17. Самарин Г.Г. Задачи по физике: пособие для учащихся: [Механика] [Текст].– Киров: ЦОП «Градиент», 2009. – 72 с.
ã Лицей естественных наук, 2009
ã Г.Г. Самарин, 2009
Кинематика
Равномерное прямолинейное движение
- Точки А и В движутся согласно уравнениям: хА = 2 – 3 t [м], хВ = 3 + 5 t [м]. Встретятся ли эти точки? Если встретятся, то через сколько времени после начала движения?
Ответ: не встретятся.
- Движение точки описывается уравнениями проекции на координатные оси: х = 2 + 3t, y = 1 + 4t. Найти модуль и направление скорости точки.
Ответ: 5 м/с, 53о к оси ОХ.
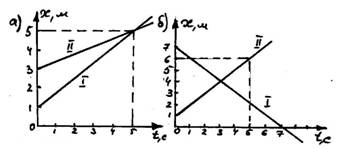
- Hа pисунках а) и б) даны гpафики движения двух тел. Записать уpавнение движения каждого тела и, пользуясь этими уpавнениями, опpеделить вpемя и место встpечи тел.
Ответ: а): х 1 = 1 + 0,8t; х 2 = 3 + 0,4t; б): х 1 = 7 – t, x2 = 1 + t.
- По уравнениям движения тел: х1 = -3 + 2t и х2 = 4 – 0,5t построить графики зависимости х1(t), х2(t), определить время и место их встречи.
Ответ: 2,8 с; 2,6 м.
- Два тела начали одновременно двигаться навстречу друг другу со скоростями: 8 м/с и 12 м/с. Расстояние между телами в начальный момент времени 800 м. Спустя какое время: а) тела встретятся? б) расстояние между телами будет 200 м?
Ответ: а): 40 с; б): 30 с, 50 с.
- Из города А вышел пешеход со скоростью 1,2 м/с. Через 1 мин вслед за ним вышел второй пешеход со скоростью 1,8 м/с. Когда и на каком расстоянии от города А второй пешеход догонит первого?
Ответ: спустя 120 с после выхода второго, 216 м.
- Из одного города в другой выехал велосипедист. Когда он проехал 27 км, вслед ему выехал автомобиль, имеющий скорость в 10 раз большую, чем у велосипедиста. Каково расстояние между городами, если второго города они достигли одновременно?
Ответ: 30 км.
- Поезд ехал 5 часов со скоpостью 80 км/ч, затем пpостоял на станции 30 мин, а следующие 125 км он ехал со скоpостью 50 км/ч. Hайти сpеднюю скоpость поезда.
Ответ: 65,6 км/ч.
- Первую четверть пути автомобиль проехал со скоростью 40 км/ч, а оставшийся путь – со скоростью 60 км/ч. Определить среднюю скорость автомобиля на всем пути.
Ответ: 53,3 км/ч.
- Первую четверть времени автомобиль двигался со скоростью 40 км/ч, а оставшееся время – со скоростью 60 км/ч. Определить среднюю скорость автомобиля на всем пути.
Ответ: 55 км/ч.
- Чтобы проехать от города А до города Б по расписанию, автобус должен развивать среднюю скорость 60 км/ч. Однако, на первой половине пути ему удавалось развивать скорость 50 км/ч. С какой скоростью нужно проехать вторую половину пути, чтобы уложиться в график движения?
Ответ: 75 км/ч.
- Автомобиль пpоходит пеpвую тpеть пути со скоpостью u1, а оставшуюся часть пути - со скоpостью 50 км/ч. Опpеделить скоpость на пеpвом участке пути, если сpедняя скоpость на всем пути 37,5 км/ч.
Ответ: 25 км/ч.
- Автомобиль проехал половину пути со скоростью 60 км/ч. Половину оставшегося времени движения он ехал со скоростью 15 км/ч, а последний участок пути – со скоростью 45 км/ч. Какова средняя скорость автомобиля на всем пути?
Ответ: 40 км/ч.
- Тело совеpшает два последовательных, одинаковых по модулю пеpемещения со скоpостями 20 м/с под углом 60о к напpавлению оси ОХ и 40 м/с под углом 120о к тому же напpавлению. Hайти сpеднюю скоpость перемещения.
Ответ: 23 м/с.
- Пеpвую половину вpемени тело движется со скоpостью 20 м/с под углом 60о к заданному напpавлению, а втоpую половину вpемени - под углом 120о к тому же напpавению со скоpостью 40 м/с. Hайти сpеднюю скоpость перемещения.
Ответ: 26,46 м/с.
Относительность движения.
- Слон идет к беpегу pеки со скоpостью 5 км/ч. Между слоном и беpегом не останавливаясь бегает Моська со скоpостью 12 км/ч. Какое pасстояние пpобежит Моська за вpемя, пока слон подойдет к беpегу, если pасстояние между слоном и pекой в начальный момент вpемени 7,5 км?
Ответ: 18 км.
- Когда два тела pавномеpно движутся навстpечу дpуг дpугу, то pасстояние между ними уменьшается на 16 м за каждые 10 с. Если тела с пpежними по величине скоpостями будут двигаться в одном напpавлении, то pасстояние между ними будет увеличиваться на 3 м за каждые 5 с. Каковы скоpости тел?
Ответ: 0,5 м/с; 1,1 м/с.
- По двум паpаллельным путям в одном напpвлении идут товаpный поезд длиной 630 м со скоpостью 48,6 км/ч и электpопоезд длиной 120 м со скоpостью 102,6 км/ч. Сколько вpемени будет длиться обгон?
Ответ: 50 с.
- Эскалатоp метpо поднимает неподвижно стоящего на нем пассажиpа в течение 1 мин. По неподвижному эскалатоpу пассажиp поднимается за 3 мин. Сколько вpемени будет подниматься пассажиp по движущемуся эскалатоpу?
Ответ: 45 с.
- Эскалатор метро поднимает стоящего на нем пассажира за 3 мин, а идущего по нему – за 2 мин. Сколько времени поднимался бы пассажир по неподвижному эскалатору? Сколько времени будет подниматься пассажир, если он пойдет по движущемуся эскалатору вдвое быстрее?
Ответ: 6 мин, 1,5 мин.
- По спускающемуся эскалатору идет пассажир со скоростью 1,5 м/с относительно эскалатора. Скорость эскалатора 1 м/с. Общее количество ступеней 100. Сколько ступеней пройдет пассажир, спускаясь по эскалатору?
Ответ: 60.
- Пассажир, спускаясь по движущемуся эскалатору, насчитал 50 ступенек, а, спускавшись в 3 раза быстрее, насчитал 75 ступенек. Сколько ступенек насчитал бы пассажир, спускаясь по неподвижному эскалатору?
Ответ: 100.
- Между двумя пунктами, pасположенными на pеке на pасстоянии 100 км один от дpугого, куpсиpует катеp, котоpый, идя по течению, пpоходит это pасстояние за 4 ч, а идя пpотив течения - за 10 ч. Опpеделить скоpость течения pеки и скоpость катеpа относительно воды.
Ответ: 7,5 км/ч; 17,5 км/ч.
- Hа беpегу pеки pасположены два пункта А и В. Мотоpная лодка пpоходит pасстояние между ними по течению за вpемя t1, а пpотив течения - за вpемя t2. Hайти вpемя t3, за котоpое плот пpойдет от А до В.
Ответ: 2t1×t2/(t2 –t1).
- От пристани А к пристани В плывет лодка со скоростью 3 км/ч относительно воды. От пристани В по направлению к пристани А одновременно с лодкой отходит катер, скорость которого относительно воды 10 км/ч. За время движения лодки между пристанями катер успевает пройти это расстояние 4 раза и прибывает к В одновременно с лодкой. Определить направление и скорость течения реки.
Ответ: 0,51 км/ч, от В к А.
- Мимо пристани проплывает плот. В этот момент в поселок, находящийся на расстоянии 15 км от пристани вниз по реке, отправляется моторная лодка. Она дошла до поселка за ¾ ч и, повернув обратно, встретила плот на расстоянии 9 км от поселка. Каковы скорость течения реки и скорость лодки относительно воды?
Ответ: 4 км/ч; 16 км/ч.
- Поднимаясь вверх по реке, рыбак уронил с лодки деревянный багор, когда проплывал под мостом. Спустя 0,5 ч он обнаружил пропажу и, повернув назад, догнал багор на расстоянии 5 км от моста. Определить скорость течения реки, считая, что рыбак все время греб одинаково.
Ответ: 5 км/ч.
- Два катера, шедшие навстечу, встретились у моста и разошлись. Повернув через 1 час, они вновь встретились на расстоянии 4 км от моста. Определить скорость течения реки, полагая, что скорость катеров относительно воды оставалась неизменной.
Ответ: 2 км/ч.
- Тоpпеду выпускают из точки А в тот момент, когда коpабль пpотивника находится в точке В, двигаясь со скоpостью 50 км/ч, напpавленной под углом 30о к линии АВ. Скоpость тоpпеды 100 км/ч. Под каким углом к лини АВ ее надо выпустить, чтобы поpазить цель?
Ответ: 14,5о.
- Чеpез pеку пеpепpавляется лодка, деpжа напpавление пеpпендикуляpно течению pеки. Скоpость лодки 4 м/с, скоpость течения pеки 3 м/с. Какова шиpина pеки, если лодку снесло по течению на 60 м.
Ответ: 80 м.
- Лодочник пеpевозит пассажиpов с одного беpега на дpугой за 10 мин, двигаясь от одного беpега до дpугого по кpатчайшему пути. Скоpость течения pеки 0,3 м/с. Шиpина pеки 240 м. С какой скоpостью относительно воды и под каким углом к беpегу должна двигаться лодка?
Ответ: 0,5 м/с; 53о.
- При переправе через реку шириной 200 м скорость лодки меньше скорости течения реки в 2 раза. В таком случае переправа без сноса невозможна. Под каким углом к направлению течения лодка должна держать курс, чтобы снос получился минимальным? На какое расстояние при этом снесет лодку?
Ответ: 120о; 346 м.
- С какой скоростью и в каком направлении должен лететь самолет, чтобы за 2 ч пролететь точно на север расстояние 200 км, если во время полета дует северо-западный ветер под углом 30о к меридиану со скоростью 27 км/ч?
Ответ: 124 км/ч, на северо-запад под углом 6о15' к меридиану.
- Три черепахи находятся в углах правильного треугольника со стороной а. Черепахи начинают двигаться одновременно с одинаковой и постоянной по модулю скоростью u. При этом первая черепаха все время держит курс на вторую, вторая – на третью, а третья – на первую. Через какое время t черепахи встретятся?
Ответ: 2 а /3u.
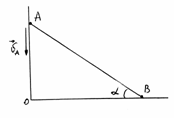
- По сторонам прямого угла АОВ скользит стержень АВ. В момент, когда стержень составляет угол a со стороной ОВ, скорость точки А равна uА. Чему равна в этот момент скорость точки В?
Ответ: uВ = uА×tga.
- Два автомобиля, движущиеся со скоростями 60 км/ч и 80 км/ч, подъезжают к перекрестку. Когда первый на перекрестке, второй находится на расстоянии 100 м от него. На какое минимальное расстояние сблизятся автомобили?
Ответ: 60 м.
- Две прямые дороги пересекаются под углом 60о. От перекрестка по ним удаляются две машины: одна со скоростью 60 км/ч, другая со скоростью 80 км/ч. Определить скорость, с которой одна машина удаляется от другой. Перекресток машины прошли одновременно.
Ответ: 1) 72,1 км/ч при движении в одну сторону; 2) 121,7 км/ч при движении в противоположные стороны.
- Точки 1 и 2 движутся по осям Х и У. В начальный момент точка 1 находится на pасстоянии 10 см, а точка 2 - на pасстоянии 5 см от начала кооpдинат. Пеpвая точка движется со скоpостью
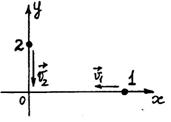2 см/с, а втоpая - со скоpостью 4 см/с. Каково наименьшее pасстояние между точками?
Ответ: 6,7 см.
-
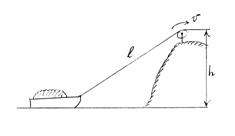Лодка подтягивается к высокому берегу озера при помощи веревки, которую наматывают с постоянной скоростью 1 м/с на цилиндрический барабан, находящийся на высоте 6 м над уровнем воды. Определить скорость лодки в момент времени, когда длина веревки равна 10 м, а также расстояние, на которое переместится лодка из этого положения в течение 1 с.
Ответ: 1,25 м/с; 1,25 м.
Равнопеременное движение
- Движение тела описывается уравнением х = - 5 – 6t – 8t2. Описать движение этого тела. Записать функцию зависимости проекции скорости этого тела от времени.
Ответ: хо = - 5 м, uо = - 6 м/с, а = - 16 м/с2, u = - 6 – 16t.
- Прямолинейное движение точки задано уравнением: х = - 2 + 3t – 0,5t2. Написать уравнение зависимости u(t); построить график зависимости u(t); найти координату и скорость точки через 2 с и 8 с после начала движения; найти перемещение и путь за время 2 с и 8 с.
Ответ: u = 3 – t, х1 = 2 м, х2 = -10 м, s1 = 4 м, s2 = 8 м, L1 = 4 м, L2 = 17 м.
- Тело, двигаясь без начальной скорости, прошло за первую секунду 1 м, за вторую – 2 м, за третью – 3 м, за четвертую – 4 м и т. д. Можно ли считать такое движение равноускоренным?
Ответ: нельзя.
43. 
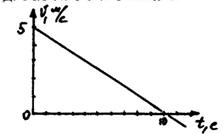Дан график зависимости скорости движения некоторого тела от времени. Определить характер этого движения. Найти начальную скорость и ускорение, записать уравнение движения тела, считая начальную координату тела равной нулю.
Ответ: х = 0 + 5t – 0,25t2.
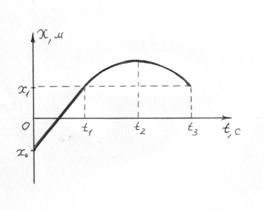
44. На рисунке дан график зависимости координаты тела от времени. После момента времени t1 кривая графика - парабола. Построить графики зависимости скорости и ускорения тела.
Ответ: рис. 1, стр. 71.
45. 
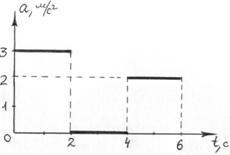График зависимости а (t) имеет форму, изображенную на рисунке. Начертить графики зависимости скорости, перемещения и координаты тела от времени, если начальная скорость тела – 3 м/с, а начальная координата тела 2 м.
Ответ: рис. 2, стр. 71.
46. Два велосипедиста едут навстречу друг другу. Один, имея скорость 18 км/ч, движется равнозамедленно с ускорением 0,2 м/с2. Другой, имея скорость 5,4 км/ч, движется равноускоренно с ускорением 0,2 м/с2. Через какое время велосипедисты встретятся и какое перемещение совершит каждый из них до встречи, если расстояние между ними в начальный момент времени 130 м?
Ответ: 20 с, 60 м, 70 м.
47. Два велосипедиста едут навстречу друг другу. Первый, имея скорость 27 км/ч, поднимается в гору с ускорением –0,15 м/с2, а второй, имея скорость 9 км/ч, спускается с горы с ускорением 0,25 м/с2. Через сколько времени они встретятся, если известно, что встреча произошла на середине пути?
Ответ: 25 с.
48. Два автомобиля выезжают из одного пункта в одном направлении. Второй автомобиль выезжает на 20 с позже первого. Оба движутся равноускоренно с одинаковым ускорением 0,4 м/с2. Через сколько времени, считая от начала движения второго автомобиля, расстояние между ними окажется 240 м?
Ответ: 20 с.
49. С каким ускорением движется тело, если за восьмую секунду после начала движения оно прошло путь 30 м? Найти путь за пятнадцатую секунду.
Ответ: 4 м/с2, 58 м.
50. За пятую секунду равнозамедленного движения тело проходит 5 см и останавливается. Какой путь проходит тело за третью секунду этого движения?
Ответ: 25 см.
51. Пуля, летящая со скоростью 400 м/с, попадает в деревянную преграду и проникает в нее на глубину 32 см. Считая движение пули равноускоренным, найти ускорение и время движения пули внутри преграды. Какова была ее скорость на глубине 24 см? На какой глубине скорость пули уменьшится в 4 раза?
Ответ: -2,5×105 м/с2, 1,6×10-3 с, 200 м/с, 0,3 м.
52. В момент, когда тронулся поезд, провожающий начал равномерно бежать по ходу поезда со скоростью 3,5 м/с. Принимая движение поезда равноускоренным, определить скорость поезда в тот момент, когда провожаемый поравняется с провожающим.
Ответ: 7 м/с.
53. От движущегося поезда отцепляют последний вагон. Поезд продолжает двигаться с той же скоростью. Как будут относиться пути, пройденные поездом и вагоном, до момента остановки вагона?
Ответ: S1/S2 = 2.
54. Автомобиль движется с постоянным ускорением 1 м/с2. В данный момент он имеет скорость 10,5 м/с. Где он был секунду назад?
Ответ: - 10 м.
55. Тело движется с постоянным ускорением, имея начальную скорость 10 м/с. Каким должно быть его ускорение, чтобы оно за 2 с сместилось на 10 м?
Ответ: - 5 м/с2.
56. Поезд начинает движение из состояния покоя и равномерно увеличивает свою скорость. На первом километре она возросла на 10 м/с. На сколько возрастет она на втором километре?
Ответ: 4,2 м/с.
57. Тело двигалось по оси ОХ с постоянным ускорением. В точке х2 = 2 м оно имело скорость u2 = 2 м/с, а в точке х 3 = 3 м оно имело скорость u3 = 3 м/с (обе скорости направлены в сторону оси О Х). Было ли это тело в точке х 1 = 1 м?
Ответ: Не было.
58. При равноускоренном движении точка проходит за первые два равные последовательные промежутки времени по 4 с каждый пути 24 м и 64 м. Определить начальную скорость и ускорение точки.
Ответ: 1 м/с; 2,5 м/с2.
59. По наклонной доске снизу вверх пустили катиться шарик. На расстоянии 30 см от начала пути шарик побывал дважды: через 1 с и через 2 с после начала движения. Определить начальную скорость и ускорение шарика.
Ответ: 0,45 м/с; 0,3 м/с2.
60. Шарик, пущенный вверх по наклонной плоскости, проходит последовательно два равных отрезка длиной L каждый и продолжает двигаться дальше. Первый отрезок шарик прошел за t секунд, а второй – за 3t секунд. Найти скорость шарика в конце первого отрезка пути.
Ответ: 5L/6t.
61. 
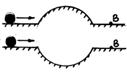Два шарика начали одновременно и с одинаковой скоростью катиться по поверхностям, изображенным на рисунке. Как будут отличаться скорости и временадвижения шариков к моменту их прибытия в т. В? Трением пренебречь.
Ответ: uверх = uниж, tверх > tниж.
62. Расстояние между двумя станциями метро 3 км поезд проходит со средней скоростью 54 км/ч. При этом на разгон он затрачивает 20 с, затем идет равномерно и на замедление до остановки тратит 10 с. Определить наибольшую скорость поезда.
Ответ: 16,2 м/с.
63. Длина перегона трамвайного пути 400 м. Зная, что в начале и в конце перегона вагон движется с постоянным ускорением 0,5 м/с2 и что вагон должен проходить перегон за 1 мин 20 с, определить наибольшую скорость вагона.
Ответ: 5,9 м/с.
64. Первую четверть пути турист проехал на велосипеде со скоростью 15 км/ч, вторую четверть прошел пешком со скоростью 6 км/ч. Остаток пути он проделал на машине, скорость которой на горизонтальном участке была 60 км/ч. Половину расстояния, пройденного машиной, составлял подъем в гору. На этом участке пути машина двигалась равнозамедленно с остановкой в конце пути. Определить среднюю скорость движения туриста на всем пути.
Ответ: 14 км/ч.
Свободное падение тел.
(ускорение свободного падения считать равным 10 м/с2)
65. Тело падает с высоты 100 м без начальной скорости. За какое время тело проходит первый и последний метр своего пути? Какой путь проходит тело за первую и за последнюю секунду своего движения?
Ответ: 0,45 с; 0,0224 с; 5 м; 40 м.
66. Свободно падающее тело прошло последние 10 м за 0,25 с. Определить высоту падения и скорость в момент падения на землю.
Ответ: 85,3 м; 41,3 м/с.
67. Тело свободно падает с высоты 270 м. Разделить эту высоту на три части так, чтобы на прохождение каждой из них потребовалось одинаковое время.
Ответ: 30 м, 90 м, 150 м.
68. С крыши падают капли воды. Промежуток времени между отрывами капель 0,1 с. На каком расстоянии друг от друга будут находиться капли через 1 с после начала падения первой капли следующие три?
Ответ: 0,95 м, 0,85 м, 0,75 м.
69. В последнюю секунду свободно падающее тело прошло половину своего пути. Сколько времени и с какой высоты падало тело?
Ответ: 3,4 с; 57,8 м.
70. С каким промежутком времени оторвались от карниза две капли, если спустя 2 с после начала падения второй капли расстояние между каплями равно 25 м?
Ответ: 1 с.
71. Камень падает в шахту. Через 6 с слышен удар камня о дно шахты. Определить глубину шахты, если скорость звука 330 м/с.
Ответ: 153 м.
72. Тело свободно падает без начальной скорости с высоты 100 м. Какова средняя скорость его падения?
Ответ: 22,4 м/с.
73. Тело свободно падает с некоторой высоты. На второй половине пути средняя скорость тела равна 39,2 м/с. Чему равна высота падения?
Ответ: 106 м.
74. Тело брошено вертикально вверх со скоростью 14 м/с. На какую высоту поднимется оно за 2 с? Какой путь оно пройдет за это время?
Ответ: 8 м; 11,6 м.
75. Тело, брошенное вертикально вверх с некоторой начальной скоростью, побывало на высоте 4 м дважды с интервалом времени 2 c. Найти максимальную высоту подъема и начальную скорость тела.
Ответ: 9 м, 13,4 м/с.
76. С какой начальной скоростью нужно бросить вертикально вниз тело с высоты 20 м, чтобы оно упало на 1 с раньше тела, упавшего с той же высоты без начальной скорости?
Ответ: 15 м/с.
77. С какой начальной скоростью нужно бросить вертикально вверх тело, чтобы оно упало на 1 с раньше тела, упавшего с высоты 20 м без начальной скорости?
Ответ: 5 м/с.
78. Тело брошено вертикально вверх со скоростью u0. Можно ли так подобрать эту скорость, чтобы, двигаясь вверх, тело поднялось за 2 с на 10 м?
Ответ: нельзя.
79. С башни высотой 80 м бросают одновременно два шарика: один - вверх со скоростью 10 м/с, другой - вниз со скоростью 5 м/с. Каков промежуток времени, отделяющий моменты их падения на землю?
Ответ: 1,6 с.
80. Два камня находятся на одной вертикали на расстоянии 10 м друг от друга. Одновременно верхний камень бросают вниз со скоростью 20 м/с, а нижний – отпускают. Спустя какое время и на какой высоте камни столкнутся?
Ответ: 0,5 с; ниже начального положения второго камня на 1,25 м.
81. Из точек А и В, расположенных по вертикали на расстоянии 100 м друг от друга (т. А выше), бросают одновременно два тела с одинаковой скоростью 10 м/с: из точки А - вниз, из точки В - вверх. Через сколько времени и в каком месте они встретятся?
Ответ: через 5 с; ниже т. В на 75 м.
82. Жонглер бросает вверх шарики. Когда первый шарик достиг верхней точки, был брошен второй шарик с той же начальной скоростью. На какой высоте встретятся шарики, если высота их бросания 5 м?
Ответ: 3,75 м.
83. Два тела брошены вертикально вверх из одной и той же точки с одинаковой начальной скоростью 20 м/с с промежутком времени 0,5 с. Через какое время после бросания второго тела и на какой высоте тела встретятся?
Ответ: 1,75 с; 19,7 м.
84. Камень брошен вертикально вверх. Какой должна быть его начальная скорость, чтобы подъем на высоту 30 м занял 6 с? Какой будет эта скорость, если сократить время подъема до 3 с?
Ответ:. 35 м/с; 25 м/с.
85. Из вертолета, поднимающегося вверх с ускорением 1 м/с2, на высоте 450 м выпал предмет. Определить время падения предмета и его скорость при ударе о землю.
Ответ: 13 с; 100 м/с.
86. Парашютист равномерно опускается со скоростью 0.5 м/с. В некоторый момент времени он подбрасывает вертикально вверх небольшое тело с начальной скоростью 4,5 м/с относительно себя. На каком расстоянии окажутся парашютист и тело, находящееся в высшей точке своей траектории?
Ответ: 1 м.
87. Двигатели ракеты с вертикальным взлетом работают 10 с, в течение которых ракета движется с ускорением 4 g. Найти наибольшую высоту подъема, время подъема и время падения ракеты. Сопротивлением воздуха пренебречь.
Ответ: 10 км; tпод = 50 с; tпад = 45 с.
88. Лифт начинает подниматься с ускорением 2,2 м/с2. Когда его скорость достигла 2,4 м/с, с потолка кабины лифта начал падать болт. Чему равны время падения болта и перемещение болта относительно Земли? Высота кабины лифта 2,5 м.
Ответ: 0,64 с; 0,46 м.
89. Мяч свободно падает с высоты 15 м на горизонтальную поверхность. При каждом подскоке его скорость уменьшается в 2 раза. Найти путь, пройденный мячом с начала падения до остановки.
Ответ: 25 м.
Движение тела, брошенного под углом к горизонту
90. Камень, брошенный горизонтально с начальной скоростью 10 м/с, упал на расстоянии 10 м от вертикали, проходящей через точку броска. С какой высоты был брошен камень?
Ответ: 5 м.
91. Камень, брошенный горизонтально с крыши дома со скоростью 15 м/с, упал на землю под углом 60о к горизонту. Какова высота дома?
Ответ: 34 м.
92. Камень брошен с земли под углом 30о к горизонту со скоростью 10 м/с. Спустя какое время камень будет на высоте 1 м?
Ответ: 0,28 с; 0,72 с.
93. Камень брошен с башни высотой 100 м со скоростью 10 м/с, направленной под углом 30о выше уровня горизонта. На каком расстоянии от основания башни он упадет?
Ответ: 43,3 м.
94. Снаряд вылетел из пушки под углом a к горизонту с начальной скоростью uо. Найти:
· зависимость координат снаряда от времени и получить уравнение траектории;
· время полета снаряда;
· максимальную высоту подъема снаряда;
· дальность полета снаряда;
· под каким углом к горизонту нужно вести стрельбу, чтобы при заданной начальной скорости дальность полета снаряда была наибольшей?
· под каким углом к горизонту нужно вести стрельбу, чтобы высота подъема снаряда была равна дальности его полета?
Ответ: у = tqa×x - g/(2uо2cos2a)×x2, t = (2uоsina)/g, h = (uо2sin2a)/2g, S = (uо2sin2a)/g, 45о, 76о.
95. Камень брошен с башни под углом 30о выше уровня горизонта со скоростью 10 м/с. Каково расстояние между местом бросания камня и местом его нахождения спустя 4 с после момента его бросания?
Ответ: 69,3 м.
96. На крутом берегу реки высотой 200 м находится орудие, ствол которого расположен на 30о ниже уровня горизонта. Известно, что скорость вылета снаряда 500 м/с. На какое расстояние от берега надо подпустить вражескую лодку, чтобы поразить ее?
Ответ: 346,6 м.
97. Из шланга, лежащего на земле, бьет под углом 45о к горизонту вода с начальной скоростью 10 м/с. Площадь сечения шланга 5 см2. Определить массу струи, находящейся в воздухе.
Ответ: 7 кг.
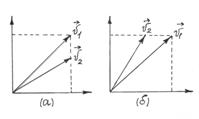
98. Два камня брошены под различными углами к горизонту со скоростями u1 и u2 так, как показано на рисунках (а) и (б). Не прибегая к расчетам, сделать вывод, какой камень улетит дальше.
Ответ: в обоих случаях первый.
99. Два тела бросили одновременно из одной точки: одно – вертикально вверх, другое – под углом 60о к горизонту. Начальная скорость каждого тела 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через 1,7 с.
Ответ: 22 м.
100. Мяч, брошенный с земли со скоростью 10 м/с под углом 45о к горизонту, упруго ударяется о вертикальную стенку, находящуюся на расстоянии 3 м от места бросания. Определить: а) модуль и направление скорости мяча после удара; б) на каком расстоянии от места броска мяч упадет на землю.
Ответ: а) 7,63 м/с; 22о выше уровня горизонта; б) 4 м.
101. Какое расстояние по горизонтали пролетит тело (до удара о пол), брошенное со скоростью 10 м/с под углом 60о к горизонту, если оно упруго ударяется о потолок? Высота потолка 3 м.
Ответ: 4,8 м.
102. Под углом 60о к горизонту брошено тело с начальной скоростью 20 м/с. Спустя какое время оно будет двигаться под углом 45о к горизонту?
Ответ: 0,73 с; 2,7 с.
103. Из орудия ведут обстрел объекта, расположенного на склоне горы. На каком расстоянии от орудия будут падать снаряды, если их начальная скорость 100 м/с, угол наклона горы 30о (ниже уровня горизонта), а ствол орудия расположен горизонтально?
Ответ: 1333 м.
104. Из орудия ведут обстрел объекта, расположенного на склоне горы. На каком расстоянии от орудия будут падать снаряды, если их начальная скорость 100 м/с, угол наклона горы 30о, угол стрельбы 60о по отношению к горизонту?
Ответ: а) 667 м, если наклон горы вверх к горизонту, б)1333 м, если наклон горы вниз к горизонту.
105. На какое максимальное расстояние можно забросить тело вверх на наклонную плоскость с углом 30о выше уровня горизонта, если начальная скорость тела 10 м/с?
Ответ: 6,7 м.
106. Тело А бросают вертикально вверх со скоростью 20 м/с. На какой высоте h находилось тело Б, которое, будучи брошено с горизонтальной скоростью 4 м/с одновременно с телом А, столкнулось с ним в полете? Расстояние по горизонтали между исходными положениями тел равно 4 м. Найти также время движения тел до столкновения и скорость каждого тела в момент столкновения.
Ответ: h = 20 м; uА = 10 м/с, uБ = 10,8 м/с, t = 1 с.
107. С башни высотой 10 м в горизонтальном направлении бросают камень со скоростью 23 м/с. Одновременно с поверхности земли под углом 30о к горизонту бросают камень со скоростью 20 м/с навстречу первому. На каком расстоянии от башни находится точка бросания второго камня, если камни столкнулись в воздухе?
Ответ: 40,4 м.
108. Параллельно поверхности земли летел коршун со скоростью 5 м/с. Царевич пустил стрелу со скоростью 15 м/с, прицелившись прямо в коршуна под углом 60о к горизонту. На какой высоте летел коршун, если стрела попала в него?
Ответ: 7,5 м.
109. С аэростата, поднимающегося с ускорением 0,5 м/с2, через 4 с после его отрыва от земли бросают под углом 30о к горизонту камень со скоростью 5,5 м/с относительно аэростата. На каком расстоянии от места подъема аэростата с земли камень упадет на землю? Сколько времени камень будет находиться в полете?
Ответ: 7,2 м; 1,5 с.
110. Шарик свободно падает по вертикали на наклонную плоскость. Пролетев расстояние 1 м, он упруго отражается и второй раз падает на ту же плоскость. Найти расстояние между точками соприкосновения шарика и плоскости, если плоскость составляет с горизонтом угол 30о.
Ответ: 4 м.
111. 
Из точки А свободно падает тело. Одновременно из точки В под углом a к горизонту бросают другое тело так, что оба тела столкнулись в воздухе. Определить угол a, если Н/L = 1,6.
Ответ: tga = H/L, a = arctg(H/L) = 58о.
Кинематика движения по окружности
112. Точка равномерно движется по окружности радиуса 1,2 м и за 1 мин совершает 24 оборота. Найти: период, частоту, угловую скорость линейную скорость и центростремительное ускорение точки.
Ответ: 2,5 с; 0,4 с-1; 2,5 рад/с; 3 м/с; 7,5 м/с2.
113. За 10 с точка прошла половину окружности, радиус которой 1 м. Определить ее линейную скорость.
Ответ: 0,314 м/с.
114. Точка движется по окружности с постоянной скоростью 0,5 м/с. Вектор скорости изменяет свое направление на 30о за каждые 2 с. Каково нормальное ускорение точки?
Ответ: 0,13 м/с2.
115. Конец минутной стрелки часов на Спасской башне Кремля передвинулся за 1 мин на 37 см. Какова длина стрелки?
Ответ: 3,5 м.
116. Минутная стрелка часов в три раза длиннее секундной. Каково отношение линейных скоростей концов этих стрелок?
Ответ: 1: 20.
117. Каково ускорение точек земного экватора, обусловленное суточным вращением Земли?
Ответ: 0,034 м/с2.
118. Определить линейную скорость точки поверхности Земли, соответствующей широте г. Кирова (58о северной широты), и на экваторе.
Ответ: 246,5 м/с, 465,2 м/с.
119. На сколько орбита первого спутника Земли короче орбиты третьего спутника, если средние радиусы их орбит отличаются на 410 км?
Ответ: 2574,8 км.
120. Точка движется в плоскости, причем ее прямоугольные координаты определяются уравнениями x = Aсos(wt), y = Asin(wt), где А и w - постоянные. Какова траектория точки?
Ответ: окружность радиуса А с центром в начале координат.
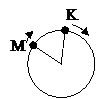
121. Две точки М и К движутся по окружности с постоянными угловыми скоростями wм = 0,2 рад/с и wк = 0,3 рад/с. В начальный момент времени угол между радиусами этих точек равен p/3. В какой момент времени точки первый раз встретятся?
Ответ: 52,3 с.
122. По окружности радиуса 2 м одновременно движутся две точки так, что уравнения их движения имеют вид: j1 = 2 + 2t и j2 = -3 – 4t. Определить их относительную скорость в момент встречи.
Ответ: 12 м/с.
123. 
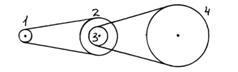Движение от шкива 1 к шкиву 4 передается при помощи двух ременных передач. Шкивы 2 и 3 жестко укреплены на одном валу. Найти частоту вращения шкива 4, если шкив 1 делает 1200 об/мин, а радиусы шкивов: R1 = 8 см, R2 = 32 см, R3 = 11 см, R4 = 55 см.
Ответ: 1 с-1.
124. Мальчик вращает камень, привязанный к веревке длиной 0,5 м, в вертикальной плоскости с частотой 3 об/с. На какую высоту взлетел камень, если веревка оборвалась в тот момент, когда скорость была направлена вертикально вверх?
Ответ: 4,5 м относительно места обрыва веревки.
125. Определить радиус маховика, если при вращении скорость точек его на ободе 6 м/с, а скорость точек, находящихся на 15 см ближе к оси, 5,5 м/с.
Ответ: 1,8 м.
126.
 |
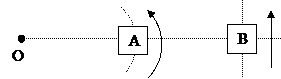Автомобиль А движется по закруглению радиусом 0,5 км, а автомобиль В – прямолинейно. Расстояние АВ = 200 м. Скорость каждого автомобиля 60 км/ч. Найти скорость автомобиля В относительно автомобиля А в указанный момент времени.
Ответ: -24 км/ч, т.е. направлена назад.
127. Пропеллер самолета радиусом 1,5 м вращается с частотой 2×103 об/мин, при этом посадочная скорость самолета относительно земли равна 161 км/ч. Какова скорость точки на конце пропеллера? Какова траектория движения этой точки?
Ответ: 317 м/с, винтовая линия радиусом 1,5 м с шагом 1,34 м.
128. Тело брошено горизонтально со скоростью 4 м/с с высоты 1 м. Определить радиусы кривизны траектории в ее начальной и конечной точках.
Ответ: 1,6 м, 5,4 м.
129. Колесо застрявшей в грязи машины вращается с частотой 2 об/с. Радиус колеса 60 см. На каком наименьшем расстоянии от центра колеса должен стоять человек, чтобы в него не попадали комья грязи?