(р-1)3р5(р+1) (2.3)
Мы утверждаем, что по этой же формуле вычисляется количество матриц, определитель которых не обращается в нуль, при условии, что 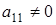 ,
,  .
.
При условии (2.2) не учитываются матрицы вида 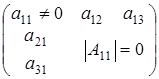 с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида
с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида  с определителем обращающимся в нуль, количество которых нужно вычесть.
с определителем обращающимся в нуль, количество которых нужно вычесть.
Докажем, что количество матриц в обоих случаях одинаково:
а) 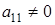 (р-1 штук),
(р-1 штук),  и
и 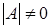 . Из (2.1) получаем равенство
. Из (2.1) получаем равенство 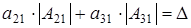 .
.
а1) Пусть  =0. Тогда
=0. Тогда  и
и 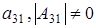 . Значит элементов
. Значит элементов  всего р-1 штук, количество невырожденных матриц
всего р-1 штук, количество невырожденных матриц  - (р-1)2р(р+1). Т.к
- (р-1)2р(р+1). Т.к  то из выражения
то из выражения  получаем равенство
получаем равенство  , т.е. хотя бы один из этих элементов не равен нулю. Пусть
, т.е. хотя бы один из этих элементов не равен нулю. Пусть 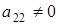 . Из того, что
. Из того, что  получаем
получаем 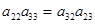 . Элементом
. Элементом  , принимающим любое значение, можем однозначно задать элемент
, принимающим любое значение, можем однозначно задать элемент 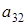 . Поэтому количество матриц удовлетворяющих этим условиям (р-1)4×р2×(р+1) штук.
. Поэтому количество матриц удовлетворяющих этим условиям (р-1)4×р2×(р+1) штук.
а2) Если  ¹0,
¹0, 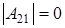 .Тогда
.Тогда  и
и 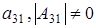 . Значит элементов
. Значит элементов  всего р-1 штук, количество невырожденных матриц
всего р-1 штук, количество невырожденных матриц  - (р-1)2р(р+1). Т.к
- (р-1)2р(р+1). Т.к  , то, из выражения
, то, из выражения 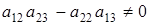 получаем
получаем 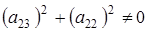 . Пусть
. Пусть 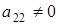 . Домножим равенство
. Домножим равенство  (
(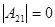 ) на
) на 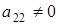 . Заменим
. Заменим  на
на 
 (из того, что
(из того, что  ). Получим равенство
). Получим равенство 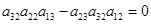 . Вынесем
. Вынесем  за скобки
за скобки  и т.к.
и т.к.  делаем вывод, что
делаем вывод, что 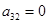 . Значит и
. Значит и 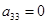 (
( ). Поэтому количество матриц удовлетворяющих этим условиям (р-1)5×р×(р+1) штук.
). Поэтому количество матриц удовлетворяющих этим условиям (р-1)5×р×(р+1) штук.
а3) Если  ¹0,
¹0, 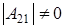 и
и  получаем (р-1)4×р2×(р+1) штук матриц удовлетворяющих этим условиям (рассуждение как в пункте а1)
получаем (р-1)4×р2×(р+1) штук матриц удовлетворяющих этим условиям (рассуждение как в пункте а1)
а4) Если  ¹0,
¹0, 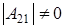 ,
,  и
и 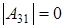 получаем
получаем
(р-1)5×р×(р+1) штук матриц удовлетворяющих этим условиям (рассуждение как в пункте а2)
а5) Если  ¹0,
¹0, 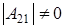 ,
,  и
и 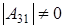 . Из того, что
. Из того, что 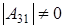 получаем
получаем  . Пусть
. Пусть 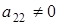 . Равенство
. Равенство  (
(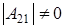 ) умножим на
) умножим на 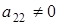 и заменим
и заменим 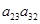 на
на 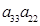 (
(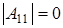 ). Получим равенство
). Получим равенство  . Вынося
. Вынося 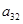 за скобки (
за скобки ( ), замечаем, что элемент
), замечаем, что элемент 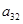 однозначно выражается через
однозначно выражается через  (
(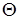 - р-1 штук). Но тогда
- р-1 штук). Но тогда  тоже выражается через эти элементы. Поэтому количество матриц удовлетворяющих этим условиям (р-1)6×р×(р+1)штук.
тоже выражается через эти элементы. Поэтому количество матриц удовлетворяющих этим условиям (р-1)6×р×(р+1)штук.
Таким образом, общее количество матриц удовлетворяющих условию пункта а) подсчитывается по формуле
(р-1)4×р×(р+1)×(р2+2р-1) (получается суммированием формул полученных в пунктах а1-а5).
б) 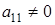 (р-1 штук),
(р-1 штук),  ((р-1)2×р×(р+1)) штук). Т.к.
((р-1)2×р×(р+1)) штук). Т.к. 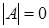 , значит
, значит  (2.4)
(2.4)
б1) Пусть  =0. Тогда из (2.4) выводится равенство
=0. Тогда из (2.4) выводится равенство
 (2.5)
(2.5)
а из (2.5) получим 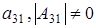 . Распишем (2.5):
. Распишем (2.5): 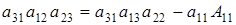 . Т.е.
. Т.е. 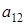 однозначно выражается через элемент
однозначно выражается через элемент 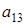 , которых может быть р штук, и через элементы
, которых может быть р штук, и через элементы 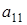 ,
, 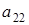 ,
, 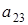 ,
,  ,
,  . Поэтому количество матриц удовлетворяющих этим условиям (р-1)4×р2×(р+1).
. Поэтому количество матриц удовлетворяющих этим условиям (р-1)4×р2×(р+1).
б2) Если  ¹0,
¹0,  .Тогда получим опять равенство (2.5) и из него
.Тогда получим опять равенство (2.5) и из него 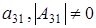 . Элементов
. Элементов  всего р-1 штук. Т.к
всего р-1 штук. Т.к  , то получаем что
, то получаем что  . Пусть
. Пусть  . Умножив равенство (2.5) на
. Умножив равенство (2.5) на 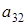 , выражая
, выражая 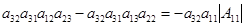 и произведя замену
и произведя замену 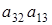 на
на  получим равенство
получим равенство  . А т.к.
. А т.к. 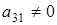 и
и  делаем вывод, что
делаем вывод, что 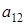 и
и 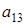 выражаются через все остальные элементы матрицы. Поэтому количество матриц удовлетворяющих этим условиям
выражаются через все остальные элементы матрицы. Поэтому количество матриц удовлетворяющих этим условиям
(р-1)5×р×(р+1) штук.
б3) Если  ¹0,
¹0, 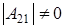 и
и  получаем (р-1)4×р2×(р+1) матриц удовлетворяющих этим условиям (рассуждения как в
получаем (р-1)4×р2×(р+1) матриц удовлетворяющих этим условиям (рассуждения как в
пункте б1)
б4) Если  ¹0,
¹0, 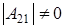 ,
,  и
и 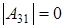 получаем
получаем
(р-1)5×р×(р+1) матриц удовлетворяющих этим условиям (рассуждения как в пункте б2)
б5) Пусть  ¹0,
¹0, 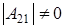 ,
,  и
и  . Из того, что
. Из того, что 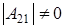 , получаем
, получаем 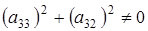 . Пусть
. Пусть  . Тогда преобразовывая (2.4) получаем, что
. Тогда преобразовывая (2.4) получаем, что  однозначно выражается через
однозначно выражается через 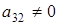 и все остальные элементы.
и все остальные элементы.
Поэтому количество матриц удовлетворяющих этим условиям (р-1)6×р×(р+1) штук.
Таким образом, общее количество матриц удовлетворяющих условию пункта б) подсчитывается по формуле
(р-1)4×р×(р+1)×(р2+2р-1) (получается суммированием формул полученных в пунктах б1-б5).
Значит формула (р-1)3р5(р+1) для случая 1) при условии (2.2) верна.
2) Пусть  ,
,  (количество их р-1),
(количество их р-1),  (количество высчитывается по формуле (1.5)) и
(количество высчитывается по формуле (1.5)) и 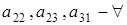 (по р штук). Тогда из (2.1) получаем
(по р штук). Тогда из (2.1) получаем
 .
.
Тогда количество таких матриц вычисляется по формуле
(р-1)3р4(р+1) (2.6)
Мы утверждаем, что по этой же формуле вычисляется количество матриц, определитель которых не обращается в нуль, при условии, что  ,
,  и
и  .
.
Но при этих условиях не учитываются матрицы вида  с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида
с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида 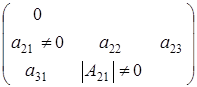 с определителем обращающимся в нуль, количество которых нужно вычесть.
с определителем обращающимся в нуль, количество которых нужно вычесть.
Докажем, что количество матриц в обоих случаях одинаково:
а)  ,
, 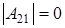 и
и  . Из (2.1) получаем равенство
. Из (2.1) получаем равенство  ,
, 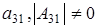 , а из того что
, а из того что 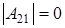 получаем что, например, элемент
получаем что, например, элемент 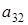 однозначно выражается через элемент
однозначно выражается через элемент  (р штук) и все остальные элементы. А значит количество матриц с данными условиями (р-1)4р2(р+1).
(р штук) и все остальные элементы. А значит количество матриц с данными условиями (р-1)4р2(р+1).
б)  ,
, 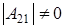 и
и  . Из (2.1) получаем равенство
. Из (2.1) получаем равенство  ,
,  . А из
. А из 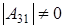 можем однозначно выразить, например, элемент
можем однозначно выразить, например, элемент 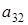 через элемент
через элемент  (р штук) и все остальные элементы. А значит количество матриц с данными условиями (р-1)4р2(р+1).
(р штук) и все остальные элементы. А значит количество матриц с данными условиями (р-1)4р2(р+1).
3) Пусть 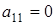 ,
, 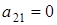 ,
,  (количество их p-1),
(количество их p-1),  (количество высчитывается по формуле (1.5)) и
(количество высчитывается по формуле (1.5)) и 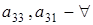 (по р штук).
(по р штук).
Тогда количество таких матриц вычисляется по формуле
(р-1)[(р-1)2р(р+1)]×р×р×р (2.7)
Этими этапами мы перебрали все случаи невырожденных матриц порядка 3. складывая формулы (2.3), (2.6) и (2.7), полученные в этапах 1), 2) и 3) получаем формулу для нахождения количества обратимых матриц порядка 3матриц над полем Zp
(р-1)3р3(р+1)(р2+р+1) (2.8)
3. Общая формула для подсчета обратимых матриц над полем Zp.
Используя алгоритм, описанный в предыдущих пунктах, для выведения формулы подсчета количества обратимых матриц, можем получить частные формулы для матриц произвольных порядков.
Например:
Для матриц порядка 4:
(р-1)4р6(р+1)(р2+р+1)(р3+р2+р+1).
Для матриц порядка 5:
(р-1)5р10(р+1)(р2+р+1)(р3+р2+р+1)(р4+р3+р2+р+1), и т.д.
Анализируя полученные результаты, можем сделать выводы, что общая формула для получения количества обратимых матриц порядка n над полем Zp выглядит так:

Данную формулу тождественными преобразованиями можно привести к виду:
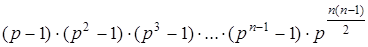
§3. Обратимые матрицы над кольцом Zn
Из теоремы доказанной в § 1 следует, что для определителей матриц A и B выполняется равенство |A·B|=|A|·|B|.
Для обратимых матриц A и B следует A · B=E.Следовательно |A · B|=|A| · |B|=|E|=1.
Таким образом, получаем: определитель обратимой матрицы является обратимым элементом.
Попытаемся сосчитать количество обратимых матриц над некоторыми кольцами вычетов по составному модулю.
Обратимые матрицы над Z4.
| * | ||||
Всего различных матриц второго порядка над Z4: 44=256.
В Z4 обратимыми элементами являются 1и3. Рассмотрим сколько обратимых матриц с определителем равным 1: |A|=ad-bc=1.
Разобьем на следующие варианты:
1. ad=3. Возможные случаи:
1) a=1 Ù d=3,
2) a=3 Ù d=1,
bc=2. Возможные случаи:
1) b=1 Ù c=2,
2) b=2 Ù c=1,
3) b=2 Ù c=3,
4) b=3 Ù c=2.
Получили с данным условием 8 обратимых матриц.
2. ad=2. Возможно 4 случая (см. предыдущий пункт).
bc=1. Возможные случаи:
1) b=c=1,
2) b=c=3.
Получили с данным условием 8 обратимых матриц.
3. ad=1. Возможно 2 случая (см. предыдущий пункт).
bc=0. Возможные случаи:
1) b=0 Ù c=1,
2) b=0 Ù c=2,
3) b=0 Ù c=3,
4) b=1 Ù c=0,
5) b=2 Ù c=0,
6) b=3 Ù c=0,
7) b=c=0,
8) b=c=2.
Получили сданным условием 16 обратимых матриц.
4. ad=0. Возможно 8 случаев (см. предыдущий пункт).
bc=3. Возможно 2 случая (см. первый пункт).
Получили с данным условием 16 обратимых матриц.
Таким образом, по данной классификации получаем 8+8+16+16+16=48 обратимых матриц, определитель которых равен 1. Аналогичную классификацию можно составить для обратимых матриц с определителем равным 3, и число таких матриц будет также равно 48.
Следовательно, из 256 квадратных матриц второго порядка над Z4 обратимыми являются 96.
Обратимые матрицы над Z6.
| * | ||||||
Всего различных матриц второго порядка над Z6: 64=1296.
В Z6 обратимыми элементами являются 1 и 5. Аналогично рассмотрим, сколько обратимых матриц с определителем равным 1:
|A|=ad-bc=1.
Разобьем на следующие варианты:
1. ad=5. Возможные случаи:
1) a=1 Ù d=5,
2) a=5 Ù d=1,
bc=4. Возможные случаи:
1) b=1 Ù c=4,
2) b=4 Ù c=1,
3) b=2 Ù c=5,
4) b=5 Ù c=2,
5) b=c=2,
6) b=c=4.
Получили с данным условием 12 обратимых матриц.
2. ad=4. Возможно 6 случаев (см. предыдущий пункт).
bc=3. Возможные случаи:
1) b=3 Ù c=1,
2) b=1 Ù c=3,
3) b=3 Ù c=5,
4) b=5 Ù c=3,
5) b=c=3.
Получили с данным условием 30 обратимых матриц.
3. ad=3. Возможно 5 случаев (см. предыдущий пункт).
bc=2. Возможные случаи:
1) b=2 Ù c=1,
2) b=1 Ù c=2,
3) b=2 Ù c=4,
4) b=4 Ù c=2,
5) b=4 Ù c=5,
6) b=5 Ù c=4.
Получили с данным условием 30 обратимых матриц.
4. ad=2. Возможно 6 случаев (см. предыдущий пункт).
bc=1. Возможные случаи:
1) b=c=1,
2) b=c=5.
Получили с данным условием 12 обратимых матриц.
5. ad=1. Возможно 2 случая (см. предыдущий пункт).
bc=0. Возможные случаи:
1) b=0 Ù c=1,
2) b=0 Ù c=2,
3) b=0 Ù c=3,
4) b=0 Ù c=4,
5) b=0 Ù c=5,
6) b=1 Ù c=0,
7) b=2 Ù c=0,
8) b=3 Ù c=0,
9) b=4 Ù c=0,
10) b=5 Ù c=0,
11) b=2 Ù c=3,
12) b=3 Ù c=2,
13) b=3 Ù c=4,
14) b=4 Ù c=3,
15) b=c=0.
Получили с данным условием 30 обратимых матриц.
6. ad=0. Возможно 15 случаев (см. предыдущий пункт).
bc=5. Возможно 2 случая (см. первый пункт).
Получили с данным условием 30 обратимых матриц.
Таким образом по данной классификации получаем 12+30+30+12+30+30=144 обратимых матриц, определитель которых
равен 1. Аналогичную классификацию можно составить для обратимых матриц с определителем равным 5, и число таких матриц будет также равно 144.
Следовательно, из 1296 квадратных матриц второго порядка над Z6 обратимыми являются 288.
Обратимые матрицы над Z8
| * | ||||||||
Всего различных матриц второго порядка над Z8: 84=4096.
В Z8 обратимыми элементами являются 1, 3, 5 и 7. Аналогично рассмотрим, сколько обратимых матриц с определителем равным 1
|A|=ad-bc=1.
Аналогично предыдущим пунктам будем придерживаться той же классификации:
1. ad=7. Возможно 4 случая.
bc=6. Возможно 8 случаев.
Получили с данным условием 32 обратимых матрицы.
2. ad=6. Возможно 8 случаев.
bc=5. Возможно 4 случая.
Получили с данным условием 32 обратимых матрицы.
3. ad=5. Возможно 4 случая.
bc=4. Возможно 12 случаев.
Получили с данным условием 48 обратимых матриц.
4. ad=4. Возможно 12 случаев.
bc=3. Возможно 4 случая.
Получили с данным условием 48 обратимых матриц.
5. ad=3. Возможно 4 случая.
bc=2. Возможно 8 случаев.
Получили с данным условием 32 обратимых матрицы.
6. ad=2. Возможно 8 случаев.
bc=1. Возможно 4 случая.
Получили с данным условием 32 обратимых матрицы.
7. ad=1. Возможны 4 случая.
bc=0. Возможно 20 случаев.
Получили с данным условием 80 обратимых матриц.
8. ad=0. Возможно 20 случаев.
bc=7. Возможно 4 случая.
Получили с данным условием 80 обратимых матриц.
Таким образом, обратимых матриц, определитель которых
равен 1 —384.
Следовательно, из 4096 квадратных матриц второго порядка над Z8 обратимыми являются 1536.
Обратимые матрицы над Z9
| * | |||||||||
Всего различных матриц второго порядка над Z9: 94=6561.
В Z9 обратимыми элементами являются 1, 2, 4, 5, 7 и 8.
1. ad=8. Возможно 6 случаев.
bc=7. Возможно 6 случаев.
Получили с данным условием 36 обратимых матриц.
2. ad=7. Возможно 6 случаев.
bc=6. Возможно 12 случаев.
Получили с данным условием 72 обратимых матриц.
3. ad=6. Возможно 12 случаев.
bc=5. Возможно 6 случаев.
Получили с данным условием 72 обратимых матриц.
4. ad=5. Возможно 6 случаев.
bc=4. Возможно 6 случаев.
Получили с данным условием 36 обратимых матриц.
5. ad=4. Возможно 6 случаев.
bc=3. Возможно 12 случаев.
Получили с данным условием 72 обратимых матриц.
6. ad=3. Возможно 12 случаев.
bc=2. Возможно 6 случаев.
Получили с данным условием 72 обратимых матриц.
7. ad=2. Возможно 6 случаев.
bc=1. Возможно 6 случаев.
Получили с данным условием 36 обратимых матриц.
8. ad=1. Возможно 6 случаев.
bc=0. Возможно 21 случай.
Получили с данным условием 126 обратимых матриц.
9. ad=0. Возможно 21 случай.
bc=8. Возможно 6 случаев.
Получили с данным условием 126 обратимых матриц.
Таким образом, обратимых матриц, определитель которых равен 1 -648.
Следовательно, из 6561 квадратных матриц второго порядка над Z9 обратимыми являются 3888.
Обратимые матрицы над Z10
| * | ||||||||||
Всего различных матриц второго порядка над Z10: 104=1000.
В Z10 обратимыми элементами являются 1, 3, 7 и 9.
1. ad=9. Возможно 4 случая.
bc=8. Возможно 12 случаев.
Получили с данным условием 48 обратимых матриц.
2. ad=8. Возможно 12 случаев.
bc=7. Возможно 4 случая.
Получили с данным условием 48 обратимых матриц.
3. ad=7. Возможно 4 случая.
bc=6. Возможно 12 случаев.
Получили с данным условием 48 обратимых матриц.
4. ad=6. Возможно 12 случаев.
bc=5. Возможно 9 случаев.
Получили с данным условием 108 обратимых матриц.
5. ad=5. Возможно 9 случаев.
bc=4. Возможно 12 случаев.
Получили с данным условием 108 обратимых матриц.
6. ad=4. Возможно 12 случаев.
bc=3. Возможно 4 случая.
Получили с данным условием 48 обратимых матриц.
7. ad=3. Возможно 4 случая.
bc=2. Возможно 12 случаев.
Получили с данным условием 48 обратимых матриц.
8. ad=2. Возможно 12 случаев.
bc=1. Возможно 4 случая.
Получили с данным условием 48 обратимых матриц.
9. ad=1. Возможно 4 случая.
bc=0. Возможно 27 случаев.
Получили с данным условием 108 обратимых матриц.
10. ad=0. Возможно 27 случаев.
bc=9. Возможно 4 случая.
Получили с данным условием 108 обратимых матриц.
Таким образом, обратимых матриц, определитель которых
равен 1 —720.
Следовательно, из 10000 квадратных матриц второго порядка над Z10 обратимыми являются 2880.
Используя выше изложенный метод, было также вычислено количество обратимых матриц для колец вычетов по модулям:10, 12, 14, 15, 16, 18, 20, 21. В результате всех вычислений были получены следующие данные (ниже также использованы формулы полученные в § 2):
| Zn | формула | количество |
| (p-1)2p(p+1) | ||
| (p-1)2p(p+1) | ||
| - | ||
| (p-1)2p(p+1) | ||
| - | ||
| (p-1)2p(p+1) | ||
| - | ||
| - | ||
| - | ||
| (p-1)2p(p+1) | ||
| - | ||
| (p-1)2p(p+1) | ||
| - | ||
| - | ||
| - | ||
| (p-1)2p(p+1) | ||
| - | ||
| (p-1)2p(p+1) | ||
| - | ||
| - |
В итоге анализа полученных результатов эмпирическим путем была получена следующая формула для вычисления количества обратимых матриц второго порядка над кольцом вычетов по произвольному модулю.
Пусть Zn - кольцо вычетов по модулю n, причем n=p1k1p2k2…pmkm,
Тогда количество обратимых матриц второго порядка равно:
(p1-1)2(p2-1)2…(pm-1)2p1p2…pm(p1+1)(p2+1)…(pm+1)(p14)k1-1(p24)k2-1…(pm4)km-1
Литература
1. Бухштаб А.А. Теория чисел. М.: Просвещение, 1966.
2. Куликов Л.Я. Алгебра и теория чисел. М.: Высшая школа, 1979.
3. Курош А. Г. Курс высшей алгебры. М.: Наука, 1975.