Умение последовательно чётко и непротиворечиво излагать свои мысли тесно связано с умением представлять сложные действия в виде организованной последовательности простых действий. Такое умение называется алгоритмическим. Оно находит своё выражение в том, что человек, видя конечную цель, может составить алгоритмическое предписание или алгоритм, в результате выполнения которого цель будет достигнута. Под алгоритмом мы будем понимать точное описание некоторой последовательности действий.
Алгоритм – это точная конечная система правил, определяющая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения (после конечного числа шагов) искомого результата.
Приведенное выше определение не является определением в математическом смысле слова, а довольно подробное описание понятия алгоритма, раскрывающее его сущность. Строгое понятие алгоритма не дается. Некоторые математики считают понятие алгоритма неопределяемым.
Значение слова алгоритм очень схожи со значением слов рецепт, процесс, метод, способ. Однако любой алгоритм, в отличии от рецепта или способа, обязательно обладает следующими свойствами.
1. Определенность. Оно означает, что каждое действие алгоритма должно быть сформулировано точно и однозначно пониматься исполнителем.
2.Понятность означает, что алгоритм должен содержать только такие действия, которые данному исполнителю понятны, то есть он умеет их исполнять.
3.Массовость означает, что алгоритм должен быть предназначен для решения любой задачи из класса однотипных задач.
4. Дискретность означает, что действия в алгоритме должны быть установлены в строго определенном порядке так. Чтобы для каждого действия, кроме последнего, можно было указать единственное, непосредственно следующее за ним.
|
|
5. Результативность означает, что выполнение всех шагов алгоритма Должно приводить к определенному результату. (как результат
подразумевается возможность, что задача не имеет решения).
6. Вообще элементарность означает, что в алгоритме на содержится действий которые нельзя представлять более простыми, так как в принципе таких действий не существует. Поэтому, под элементарностью будем понимать запись алгоритма в виде таких действий, которые данному исполнителю нет смысла представлять более простыми. 7.Конечность означает, что любой алгоритм состоит из конечного числадействий.
8. Эффективность (устанавливается только при наличии двух или более алгоритмов при решении одной и той же задачи) означает, что эффективным является тот алгоритм, в котором меньше действий или действия которого более простые.
Алгоритм – это жёсткое предписание о выполнении в определённой последовательности элементарных операций для решения познавательных задач. Он может использоваться как в готовом виде, так и самостоятельно отыскиваться школьниками. Примерами алгоритмов в начальных классах являются алгоритмы выполнения письменных действий сложения, вычитания, умножения и деления. Учитель может предложить ученикам и неалгоритмическое предписание, которое содержит рекомендации и общие принципы работы.
Составление алгоритмических предписаний (алгоритмов) сложная задача, поэтому начальный курс математики не ставит своей целью ее решение. Но определенную подготовку к ее достижению он может взять на себя, способствуя тем самым развитию логического мышления школьников.
|
|
В настоящее время алгоритмическая грамотность необходима каждому. Формирование алгоритмической грамотности должно осуществляться на основе логических знаний и умений учащихся. Учитывая связи между элементами логической и алгоритмической грамотности, предлагаем следующий план реализации единой логико-алгоритмической линии в курсе математики начальной школы:
лог.: 1. Знание точного смысла слов: и, или, все, каждый, некоторые.
2. Умение сравнивать.
3. Умение узнавать предмет по данным признакам.
4. Умение устанавливать отношение общего и частного.
алг.: 5. Понимание сущности алгоритма, его свойств.
6. Наглядное представление (изображение) алгоритма.
лог.: 7. Умение распределять предметы по определенным признакам
в группы (группировка предметов).
алг.: 8. Знакомство с основными типами алгоритмов.
алг.: 9. Умение четко исполнять алгоритм.
10. Умение преобразовывать алгоритм.
11. Умение выбирать рациональный алгоритм.
лог.: 12. Умение получать умозаключение.
13. Умение обосновывать умозаключение.
14. Умение составлять алгоритм.
15. Умение проверять правильность алгоритма.
Все эти умения основаны на мыслительных операциях: анализе, синтезе, сравнении, обобщении, …
Развитие умения использовать и составлять алгоритм – это основа компьютерной грамотности, а, следовательно, является необходимым умением современного человека. Воспитание алгоритмического мышления начинается в первом классе, где учеников знакомят с простейшими алгоритмами. Например, алгоритм заваривания чая, перехода через дорогу, режим дня. Всё это можно представить в виде алгоритм.
|
|
2 вопрос.Раскройте содержание первого этапа процесса формирования алгоритмического мышления учащихся. Приведите примеры различных упражнений и дидактических игр, которые можно использовать с этой целью.
Развитие умения использовать и составлять алгоритм – это основа компьютерной грамотности, а, следовательно, является необходимым умением современного человека. Воспитание алгоритмического мышления начинается в первом классе, где учеников знакомят с простейшими алгоритмами. Например, алгоритм заваривания чая, перехода через дорогу, режим дня. Всё это можно представить в виде алгоритма.
Эти алгоритмы могут быть представлены как в виде последовательности картинок, так и сформулированы в виде предложений. Важно в общем действии выделить последовательность шагов.
Детей знакомят с различными видами алгоритмов:
I. Линейный, когда последовательность действий выполняется в строго определенном порядке, однократно.
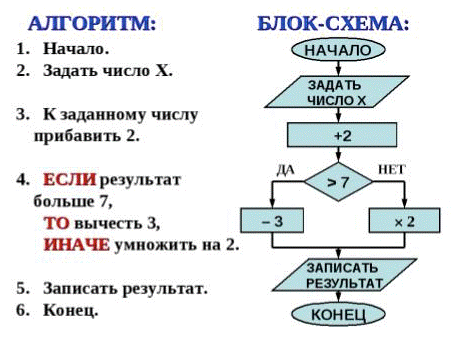
II. Разветвляющийся алгоритм характеризуется тем, что существует условие, которое необходимо проверить, и если оно выполняется, то исполняется одна последовательность шагов, если нет, то другая.
III. Циклический алгоритм содержит часть действий, которые необходимо повторить несколько раз, пока не будет реализовано некоторое условие. Именно алгоритмы помогают ребёнку объяснить сложные явления в доступной форме, воспроизводить необходимую информацию
Приведем примеры:
1. Переход через улицу по пешеходному переходу со светофором.
1.1 Остановиться на тротуаре перед светофором
1.2 Посмотреть на светофор
1.3 Посмотреть направо и налево
1.4 Перейти пешеходный переход, если горит зеленый
2. Создание презентации на компьтере.
2.1 Включить компьютер
2.2 Открыть программу для создания презентаций
2.3 Вставить нужные картинки в презентацию
2.4 Ввести нужный текст
3. Покупка конфет в магазине.
3.1 Пошел в магазин
3.2 Нашел в магазине конфеты
3.3 Купил в магазине конфеты
3.4 Пошел домой
4 «Сборы в школу».
4.1 Встаем, когда звенит будильник
4.2 Умываемся
4.3 Чистим зубы.
4.4 Делаем зарядку.
4.5 Одеваемся.
4.6 Кушаем.
4.7 Обуваемся и идем в школу.
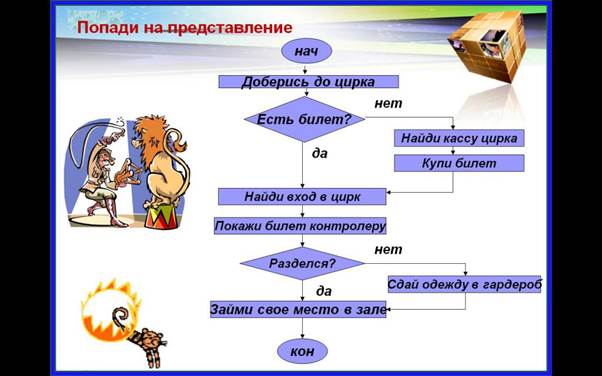
5.Попади на представление
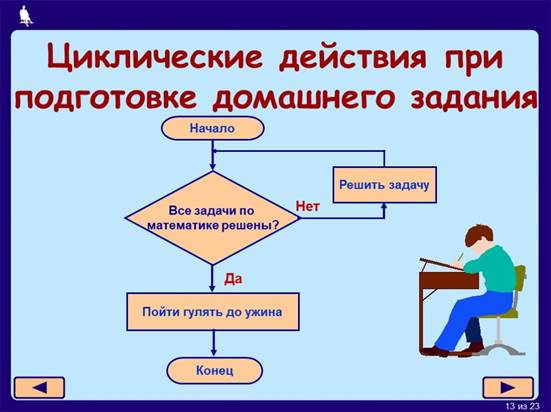
6.Подготовка домашнего задания
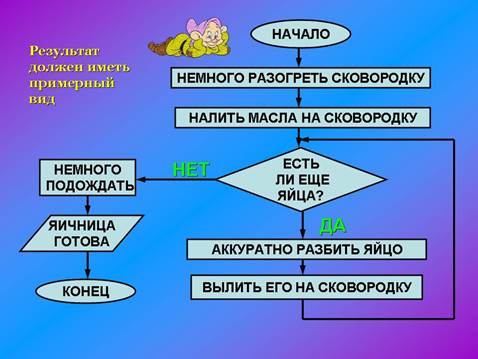
7.Приготовление яичницы
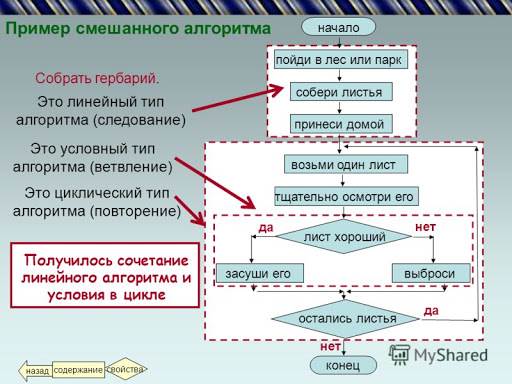
8.Собрать гербарий
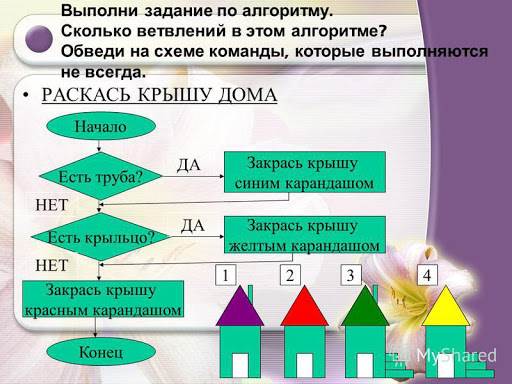
9.Раскрась крышу дома
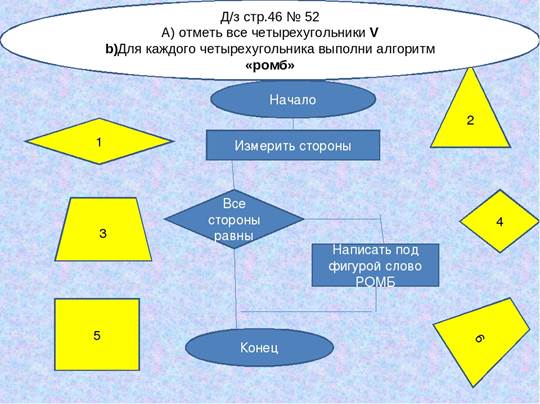
10.Алгоритм “Ромб”
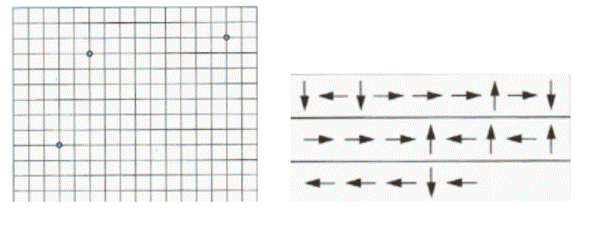
11.УМК: «Школа 2100», учебник по информатике, 2 класс. 1 ч. Горячев А.В. Диктант по клеточкам. Нарисуй каждую команду, соблюдая
последовательность Команды
Вопрос.
Покажите возможность использования алгоритмов при изучении основных математических понятий по темам: а) нумерация; б) арифметические действия; в) задачи; г) геометрический материал; д) величины; е) алгебраический материал. Приведите примеры таких алгоритмов.
Рассмотрим примеры заданий:
A. Нумерация
1. Сравнение многозначных чисел
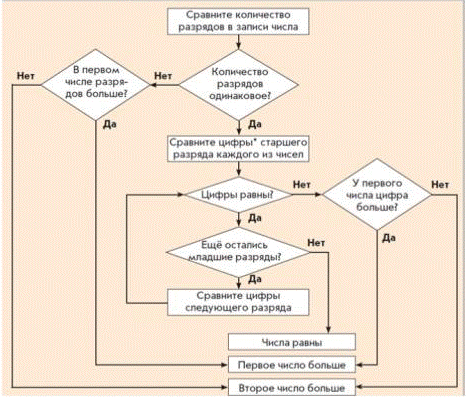
2. Разбей числа на классы.
У нас есть число 58 363 939 363.
1. Отсчитать справа по три цифры
2. Назвать класс единиц
3. Назвать класс тысяч
4. Назвать класс миллионов
5. Назвать класс миллиардов
3. Чтение многозначных чисел.
1. разбить число на классы. Отсчитывая справа по три цифры;
2.прочитать, сколько в числе единиц каждого класса, начиная с высшего.
Пример:
7300 = 7 тыс. 3 сот.
1. Число 7 относится к классу тысяч, разряд – единицы тысяч;
2. число 3 относится к классу единиц, разряд – сотни единиц,
3. 0 относится к первому классу, разряд – десятки единиц
4. 0 единиц относится к классу единиц.
B. Арифметические действия
1. 100 + 15 – 40 + 20
Чтобы найти ответ данного выражения нужно:
1.Сложить числа 100 и 15.
2. Из полученной суммы вычесть 40.
3. К результату прибавить 20.
2. 7 * (4+5): 3
Чтобы найти ответ данного выражения нужно:
1. Сложить числа 4 и 5.
2. Из полученной суммы умножить на 7.
3. К результату разделить 3.
3. 21+2*4-9

C. Задачи
Алгоритм решения задачи:
1. Чтение задачи
2. Понимание смысла задачи
3. Вопрос задачи
4. План решения задачи (краткая запись)
5. Решение (с пояснением)
6. Ответ
Рассмотрим примеры:
Простые задачи:
1. Задача на нахождение неизвестного уменьшаемого
В саду были розы. 4 розы срезали, и осталось ещё 3 розы Сколько роз было в саду?
Было –? р.
Срезали – 4 р.
Осталось – 3 р.
3 + 4 = 7 (р.)
Рассуждай так: Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Ответ: 7 роз цвели в саду.
2. Задача на умножение
В одном наборе 3 ручки. Сколько ручек в 7 наборах?
1н.- 3 р.
7н. -? р.
Рассуждай так: 3 ручки повторяются 7 раз, значит,
3 • 7 = 21(р.)
Ответ: 21 ручка в 7 наборах.
Составные задачи:
3. Задача на нахождение остатка
У Вали в двух коробках по 8 ручек, 10 ручек Валя подарила. Сколько ручек осталось у Вали?
Было — 2 к. по 8 р.
Подарила —10 р.
Осталось—? р.
Рассуждай так: Чтобы определить, сколько ручек осталось у Вали, надо знать, сколько ручек было, и сколько она их подарила. Сколько ручек Валя подарила, известно. Узнаем, сколько ручек было у Вали.
1) 8 • 2 =16 (р.) — было у Вали
2) 16 – 10 = 6 (р.)
8 • 2-10 = 6 (р.)
Ответ: 6 ручек осталось у Вали.
4. Задача на деление суммы на число и числа на сумму
15 белых роз и 10 розовых поставили в вазы по 5 роз каждую. Сколько потребовалось ваз?
Б. – 15 р.? в. по 5 роз
Р. – 10 р.
В. Всего роз
Рассуждай так: Чтобы определить, сколько нужно ваз, надо знать, сколько всего было белых и розовых роз.
1. 10 = 25 (р.) – поставили в вазы
2)25: 5 = 5 (в.)
(15 + 10):5 = 5 (в.)
Ответ: 5 ваз потребовалось
D. Геометрический материал
1. Построение прямоугольника

2.Построение треугольника

3. Построение отрезка

4. Построение окружности

E. Величины
1. Измерение S прямоугольника

2. Измерение P прямоугольника

F. Алгебраический материал
2. Решение уравнения

3. Решение составного уравнения
1. Прочитай уравнение
2. Чем выражен результат
3. Упрости правую часть
4. Запиши полученное простое уравнение
5. Реши простое уравнение
6. Сделай проверку
Пример:
x + 52 = 120: 2
x + 52 = 60
x = 60 – 52
x = 8
8 + 52 = 120: 2
60 = 60
Ответ: x = 8.