Последовательность проектировочного расчета конической зубчатой передачи

Расчет прочности зубьев по контактным напряжениям.

Для косозубых передач удельная нагрузка

.

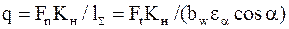По аналогии с прямозубым колесом получаем

.

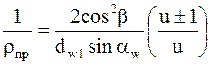Сравнивая отношение 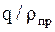в формуле для прямозубых и косозубых колес, а также учитывая, что у последних отсутствует зона однопарного зацепления, находим

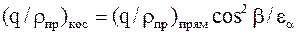
или

.

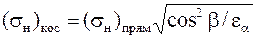Обозначим

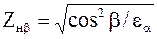
- коэффициент повышения прочности косозубых передач по контактным напряжениям. В соответствии с формулой для косозубых передач получаем

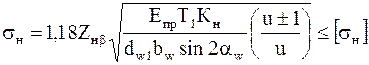
При проектном расчете 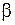и 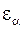неизвестны. Поэтому величину 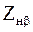в формуле предварительно оценивают приближенно. При некоторых средних значениях 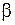=12°, 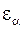=1,5 получаем 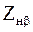~0,8. Тогда для косозубых передач

,

.

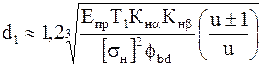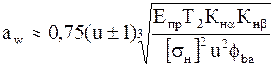Расчет конических прямозубых передач на контактную прочность

В основу данного расчета берется формула в параметрах эк­вивалентной цилиндрической прямозубой передачи по среднему дополнительно­му конусу

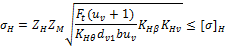
Используем связь тригонометрических функций для определе­ния передаточного числа и делительного диаметра эквива­лентного колеса .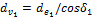

После подстановки в исходную формулу значени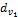й и 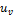и несложных преобразований получим формулу проверочного расчета для стальных пря­мозубых конических колес

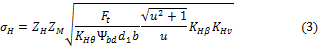
или, заменив 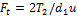; 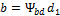, получим:

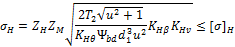
Z=Z_H Z_M=462 10³Па^1/2 (для стальных колес), (4)

где 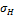— возникающее нормальное контактное напряжение, МПа; d₁ — средний делительный диаметр шестерни, мм; T₂ — вращающий момент на колесе, Нмм; Z_H— коэффициент, учитывающий форму сопряжения по­верхности зубьев; Z_M — коэффициент, учитывающий механические свойст­ва материала; Ψ_bd— коэффициент ширины (длины) зуба; u — передаточное число; K_Hθ = 0,85 — коэффициент, учитывающий снижение контактной прочности конической передачи по сравнению с прямозубой; 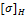— допускаемое контактное напряжение. Из двух значе­ний 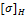выбирается меньшее.

Проектировочный расчет.

Решая уравнение относительно d₁ запишем

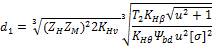
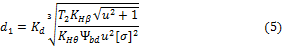
где 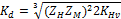— вспомогательный коэффициент (для стальных прямозубых конических колес K_d = 78 МПа^1/3).

Краткие теоретические и справочно-информационные материалы по теме:

У косозубых колес зубья располагаются не по образующей делительного цилиндра, а составляют с ней некоторый угол 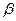. Оси колес при этом остаются параллельными. Для нарезания косых зубьев используют инструмент такого же исходного контура, как и для нарезания прямых. Поэтому профиль косого зуба в нормальном сечении 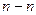совпадает с профилем прямого зуба. Модуль в этом сечении должен быть также стандартным.

В торцовом сечении 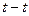параметры косого зуба изменяются в зависимости от угла :

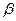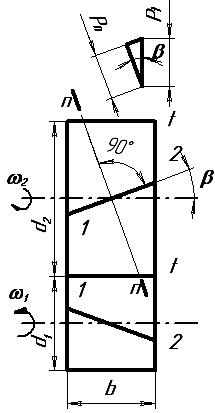
Рисунок 11 - Геометрические параметры косозубой цилиндрической передачи

окружной шаг ,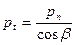

окружной модуль ,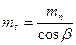

делительный диаметр .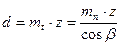

Индексы n и t приписывают параметрам в нормальном и торцовом сечениях соответственно.

Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято определять через параметры эквивалентного прямозубого колеса.

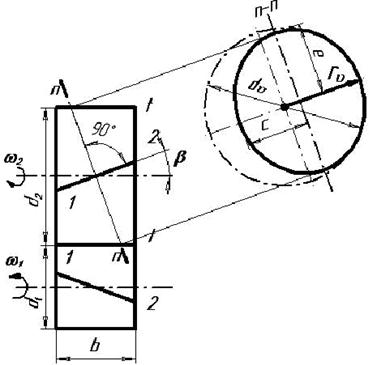
Рисунок 12 – Определение эквивалентных параметров

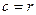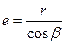Нормальное к зубу сечение образует эллипс с полуосями и , где 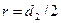. В зацеплении участвуют зубья, расположенные на малой оси эллипса, так как второе колесо находится на расстоянии 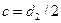. Радиус кривизны эллипса на малой оси:

.

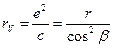В соответствии с этим, форма косого зуба в нормальном сечении определяется эквивалентным прямозубым колесом, диаметр которого:

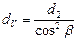
и число зубьев: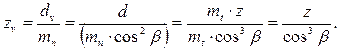

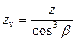
Последовательность проектировочного расчета конической зубчатой передачи