Задача 1 Рассчитать кодовое расстояние между комбинациями
а) 1101100 и 1011001;
б) 1011001 и 0100110.
Решение
Кодовое расстояние между i -ю и j -ю кодовыми комбинациями 
определяется по формуле
,
а) 1 1 0 1 1 0 0
1 0 1 1 0 0 1
--------------------
0 1 1 0 1 0 1 
.
б) 1 0 1 1 0 0 1
0 1 0 0 1 1 0
--------------------
1 1 1 1 1 1 1 
.
Задача 2
Построить все разрешенные кодовые комбинации для кода Хемминга (9,5), если проверочные разряды располагаются после информационных и
Решение
Число разрешенных кодовых комбинацийпри наличии т =5информационных разрядов в первичном коде равно
.
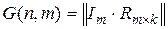
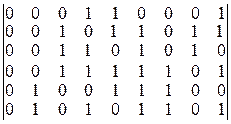
Задача 3
Задана порождающая матрица
Составить проверочную матрицу.
Решение
Матрица контрольных разрядов
,
Транспонированная матрица контрольных разрядов
Проверочная матрица
.
Задача 4.
Принимается сообщение 
1 1 0011110.
Проверочная матрица имеет вид
.
Определить искаженный разряд.
Решение
Искажен 2-й разряд
110011110
100011110.
Задача 5. Закодировать сообщение 10110 кодом Хэмминга.
Решение
Код Хэмминга записывается как
Для кодирования данного сообщения длиной m = 5 потребуется 
-проверочных разрядов. Необходимо, чтобы выполнялось условие:
2k ≥ n+1, n – число полученных разрядов,
Если принять 
,
23 =8;
тогда n=8-1=7; 
7-5=2. 22 < 7+1 неравенство не выполняется.
Примем 
,
24 =16;
тогда n=16-1=15; 15-5=10. 210 ≥ 15+1 неравенство выполняется.
24 ≥ n+1, n=4+5=9.
Получен код (9,5)
Расположим проверочные разряды в следующем порядке:
На 1-м месте проверочный разряд 
, на 2-м 
, на 4-м 
, на 8-м 
.
Переведем номера разрядов в двоичную систему счисления и поставим им в соответствие проверочные и информационные разряды
1 - 0 0 0 1 -
2 - 0 0 1 0 -
3 - 0 0 1 1 - 
1
4 - 0 1 0 0 -
5 - 0 1 0 1 - 
0
6 - 0 1 1 0 - 
1
7 - 0 1 1 1 - 
1
8 - 1 0 0 0 -
|
|
9 - 1 0 0 1 - 
0
Выпишем разряды у которых первый разряд равен 1
= 1, 3, 5, 7, 9.
Выпишем разряды у которых второй разряд равен 1
= 2, 3, 6, 7.
Выпишем разряды у которых третий разряд равен 1
= 4, 5, 6, 7.
Выпишем разряды у которых четвертый разряд равен 1
= 8, 9.
В последней строке оказался 1 информационный разряд. Переместим 7-й разряд из первой строки в последнюю:
= 1, 3, 5, 9;
=7, 8, 9.
Получим проверочные разряды.
Для получения первого проверочного разряда суммируем все разряды первой строки, кроме первого, т.е. 3, 5, 9:
.
Для получения второго проверочного разряда суммируем все разряды второй строки, кроме первого, т.е. 3, 6, 7:
.
Для получения третьего проверочного разряда суммируем все разряды третьей строки, кроме первого, т.е. 5, 6, 7:
.
Для получения четвертого проверочного разряда суммируем все разряды четвертой строки, кроме первого, т.е. 7, 8, 9:
.
Задача 6 Пользуясь кодом Хэмминга найти ошибку в сообщении и декодировать сообщение
а) 111001010;
б) 100000001.
Решение
а)
Выпишем разряды у которых первый разряд равен 1
= 1, 3, 5, 7, 9.
Выпишем разряды у которых второй разряд равен 1
= 2, 3, 6, 7.
Выпишем разряды у которых третий разряд равен 1
= 4, 5, 6, 7.
Выпишем разряды у которых четвертый разряд равен 1
= 8, 9.
В последней строке оказался 1 информационный разряд. Переместим 7-й разряд из первой строки в последнюю:
= 1, 3, 5, 9;
=7, 8, 9.
Т.к. 7-й разряд был перемещен, то ему вместо 0 1 1 1 соответствует число 1 1 1 0.
|
|
Суммируем все разряды 1-й строки
;
Суммируем все разряды 2-й строки
;
Суммируем все разряды 3-й строки
;
Суммируем все разряды 4-й строки
.
Получили синдром 1 1 1 0. ему соответствует число 7. Искажен 7-й разряд
111001 0 10 исправляем
111001 1 10.
Исключаем 1, 2 и 4-й разряды, получим число 10110
б)
= 1, 3, 5, 9.
= 2, 3, 6, 7.
= 4, 5, 6, 7.
= 7, 8, 9.
Суммируем все разряды 1-й строки
;
Суммируем все разряды 2-й строки
;
Суммируем все разряды 3-й строки
;
Суммируем все разряды 4-й строки
.
Получили синдром 1 0 0 0. Ему соответсвует число 8. искажен 8-й разряд
1000000 0 1 исправляем
1000000 1 1.
Исключаем 1, 2 и 4-й разряды, получим число 00001.
Задача 7. Закодировать данное слово кодом Хэмминга.
1001 0001 1101 1110 0000 000
РЕШЕНИЕ. Для кодирования данного сообщения длиной m = 23 потребуется k = 5
дополнительных разряда, т.е. на выходе получим сообщение длиной n = 28 (количество
дополнительных разрядов подбирали из соотношения 2k ≥ n+1, n – число полученных разрядов, k – число дополнительных разрядов).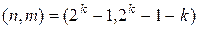 
Пусть закодированное сообщение имеет вид
b28 b27 b26 b25 b24 b23 b22 b21 b20 b19 b18 b17 b16 b15 b14 b13 b12 b11 b10 b9 b8 b7 b6 b5
b4 b3 b2 b1,
причем разряды b1, b2, b4, b8, b16 будут контрольными, а остальные информационными.
Помещаем в информационные разряды разряды исходного числа по порядку, т.е.
b3 =1, b5 = 0, b6 = 0, b7=1,
b9=0, b10 =0, b11=0, b12=1,
b13= 1, b14=1, b15=0, b17=1,
b18=1, b19=1, b20=1, b21=0,
b22=0, b23=0, b24=0, b25=0,
b26=0, b27=0, b28=0.
Теперь найдем значения контрольных разрядов.
Введем для удобства следующие множества:
V1 = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27… - все числа у которых первый разряд
|
|
равен 1
V2 = 2, 3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23, 26, 27… - все числа, у которых второй разряд
равен 1
V3 = 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23, 28… - все числа, у которых третий разряд
равен 1
V4 = 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27, 28… - все числа, у которых четвертый
разряд равен 1,
V5 = 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28 … - все числа, у которых пятый
разряд равен 1.
Далее под + будем понимать сложение по модулю 2.
Тогда b1 = b3+b5+b7+b9+b11+b13+b15+b17+b19+b21+b23+b25+b27 = 1 (все разряды из
V1, кроме первого)
b2 = b3+b6+b7+b10+b11+b14+ b15+ b18+ b19+ b22+ b23+ b26+ b27 = 1 (все разряды из
V2, кроме первого)
b4 = b5+b6+b7 +b12+b13+ b14+ b15+ b20 +b21+b22+b23+b28 = 1 (все разряды из V3,
кроме первого)
b8 = b9+b10+b11+b12+b13+b14+b15+b24+b25+b26+b27+b28 = 1 (все разряды из V4,
кроме первого),
b16 = b17+b18+b19+b20+b21+b22+b23+b24+b25+b26+b27+b28 = 0 (все разряды из V5,
кроме первого).
Таким образом, получили код 1111 0011 0001 1100 1111 0000 0000.
Задача 8. Пользуясь кодом Хэмминга найти ошибку в сообщении.
1111 1011 0010 1100 1101 1100 110.
РЕШЕНИЕ. Сообщение состоит из 27 символов, из них 22 информационные, а 5 – контрольные. Это разряды b1 = 1, b2 = 1, b4 = 1, b8 = 1, b16=0.
Вычислим число J для обнаружения ошибки:
Введем для удобства следующие множества:
V1 = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27… - все числа у которых первый разряд равен 1
V2 = 2, 3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23, 26, 27… - все числа, у которых второй разряд равен 1
V3 = 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23 … - все числа, у которых третий разряд равен 1
V4 = 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27 … - все числа, у которых четвертый разряд равен 1,
V5 = 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 … - все числа, у которых пятый разряд
равен 1.
Разряды числа J определяются следующим образом:
j1 = b1 + b3+b5+b7+b9+b11+b13+b15+b17+b19+b21+b23+b25+b27 = 1
j2 = b2+ b3+b6+b7+b10+b11+b14+ b15+ b18+ b19+ b22+ b23+ b26+ b27= 0
j3 = b4+ b5+b6+b7 +b12+b13+ b14+ b15+ b20 +b21+b22+b23 = 0
j4 = b9+b10+b11+b12+b13+b14+b15+b24+b25+b26+b27 = 0,
j5 = b16+ b17+b18+b19+b20+b21+b22+b23+b24+b25+b26+b27 = 1
то есть число J=100012 = 1710.
Таким образом, ошибка произошла в семнадцатом разряде переданного числа, следует 1 заменить на 0. Получим
1111 1011 0010 1100 0101 1100 110
Теперь удалим контрольные разряды. Получим
1101 0010 1100 1011 1001 10 - переданное число.
Задача 9
Построить кодирующее устройство кода Хэммигна для правила
= 1, 3, 5, 9. = 2, 3, 6, 7. = 4, 5, 6, 7. = 7, 8, 9.
.
.
.
.