Федеральное государственное бюджетное образовательное учреждение
Высшего образования
«Волжская государственная академия водного транспорта»
(ФГБОУ ВО «ВГАВТ»)
Пермский филиал
«Утверждаю»
Зав. Кафедрой
____________/ Е.В. Конина /
«» _______________ 20014г.
МАТЕМАТИКА
Справочный материал (основные формулы.)
Справочный материал составлен
ст. преподавателем Абраменковой В.П.
Пермь, 2014г.
Аналитическая геометрия.
Прямая на плоскости.
1. Общее уравнение прямой: 
2. Векторное уравнение прямой (проходящей через точку 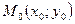 и перпендикулярно вектору
и перпендикулярно вектору  ):
): 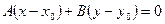
3. Каноническое уравнение прямой (проходящей через точку 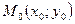 и параллельно вектору
и параллельно вектору  ):
): 
4. Уравнение прямой, проходящей через две различные точки: 
5. Уравнение прямой с угловым коэффициентом: y = kx + b, где 
6. Уравнение прямой, проходящей через точку 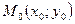 в заданном направлении:
в заданном направлении:

7.Уравнение в отрезках на осях: 
 8. Параметрическое уравнение прямой:
8. Параметрическое уравнение прямой: 


9. Расстояние от точки 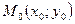 до прямой Ax + By + C = 0
до прямой Ax + By + C = 0
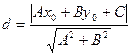
Угол между прямыми, условие параллельности и перпендикулярности прямых.
| Вид уравнения | Угол между прямыми | Условие прямых прямых
| Условие прямых прямых
|


| 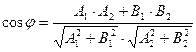
| 
| 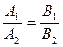
|


| 
| 
| 
|


|  
| 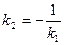
| 
|
Прямая и плоскость в пространстве.
Векторы в пространстве
1.Скалярное произведение векторов:  и
и 

2. Векторное произведение векторов:

3. Смешанное произведение векторов:

 х1 у1 z1
х1 у1 z1

 = х2 у2 z2
= х2 у2 z2
х 3 у3 z3
Прямая на плоскости.
1. Общее уравнение плоскости: Ax + By + Cz + D = 0,
где  - нормальный вектор
- нормальный вектор
2. Угол между плоскостями:  и
и 

3. Условие параллельности плоскостей: 
4. Условие перпендикулярности плоскостей: 
5. Расстояние от точки  до плоскости Ax + By + Cz + D = 0
до плоскости Ax + By + Cz + D = 0

6. Уравнение плоскости, проходящей через точку  и перпендикулярно вектору
и перпендикулярно вектору 

7. Уравнение плоскости, проходящей через три точки

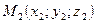


 х - х1 у – у1 z – z1
х - х1 у – у1 z – z1
 х2 - х1 у2 – у1 z2 – z1 = 0
х2 - х1 у2 – у1 z2 – z1 = 0
х 3- х1 у3 – у1 z3 – z1
8. Уравнение плоскости, проходящей через две точки 
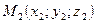 и параллельно вектору
и параллельно вектору 

 х - х1 у – у1 z – z1
х - х1 у – у1 z – z1
 х2 - х1 у2 – у1 z2 – z1 = 0
х2 - х1 у2 – у1 z2 – z1 = 0
a 1 a2 a 3
9. Уравнение плоскости, проходящей через точку  и параллельно двум векторам
и параллельно двум векторам 


 х – х0 у – у0 z – z0
х – х0 у – у0 z – z0
 a 1 a2 a 3 = 0
a 1 a2 a 3 = 0
b 1 b2 b 3
Прямая на плоскости.
1. Прямая, как пересечение двух плоскостей:



2. Уравнение прямой, проходящей через две точки 
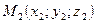
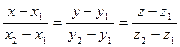
3. Каноническое уравнение прямой (проходящей через точку 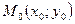 и параллельно вектору
и параллельно вектору 

4. Угол между прямыми: 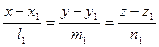 и
и 

5. Условие параллельности прямых: 
6. Условие перпендикулярности плоскостей: 
7. Условие компланарности двух прямых (нахождение в одной плоскости):

 х2 - х1 у2 – у1 z2 – z1
х2 - х1 у2 – у1 z2 – z1
 l1 m1 m2 = 0
l1 m1 m2 = 0
l2 n1 n2
Прямая и плоскость.
1.Угол между прямой  и плоскостью
и плоскостью 

2. Условие параллельности прямой и плоскости: 
3. Условие перпендикулярности прямой и плоскости: 
Кривые второго порядка
Окружность.
- С центром в начале координат:

- С центром в т. О1(а; b)

Эллипс.
- С фокусами на оси Ох:
 , где a, b – оси эллипса.
, где a, b – оси эллипса.
F1(-c; 0) и F2(c; 0) – фокусы
Связь между параметрами: 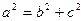
Эксцентриситет: 
С фокусами на оси Оу: 
Гипербола
1.С фокусами на оси Ох:  , где a – действительная ось, b – мнимая ось
, где a – действительная ось, b – мнимая ось
F1(-c; 0) и F2(c; 0) – фокусы
Связь между параметрами: 
Эксцентриситет:  , уравнение асимптот
, уравнение асимптот 
2.С фокусами на оси Оу: 
Парабола с вершиной в начале координат.
1. Ветви направлены вправо:  , уравнение директрисы: х = - р/2
, уравнение директрисы: х = - р/2
2. Ветви направлены влево:  , уравнение директрисы: х = р/2
, уравнение директрисы: х = р/2
3. Ветви направлены вверх:  , уравнение директрисы: у = - р/2
, уравнение директрисы: у = - р/2
4. Ветви направлены вниз:  , уравнение директрисы: у = р/2
, уравнение директрисы: у = р/2
Парабола со смещенной вершиной А(a;b).
1. Ветви направлены вправо: 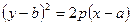
2. Ветви направлены влево: 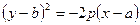
3. Ветви направлены вверх: 
4. Ветви направлены вниз: 
Таблица производных.
1.  2.
2. 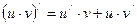
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19. 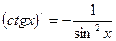 20.
20. 
21.  22.
22. 
23. 
 24.
24. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
31.  32.
32. 
33.  34.
34. 
35.  36.
36. 
37. 
Таблица интегралов.
Свойства:
10.  20.
20.  ,
, 
30. 
40.  50.
50. 
Формулы интегрирования:
1. 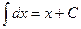 2.
2. 
3.  4.
4. 

5.  6.
6. 
7. 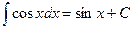 8.
8. 
9.  10.
10. 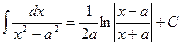
11.  12.
12. 
13. 
Определенный интеграл.
Формула Ньютона-Лейбница: 
Свойства:
1. 
2. 
3. 
4. 