Сущность (entily) – это именованный класс однотипных объектов.
Поскольку термином сущность обозначают класс объектов, можно также встретить определение класса сущностей, которое является синонимичным термину сущность. Сущность определяет собой некоторый тип сложной структуры данных, то есть наличие определенных полей (атрибутов), их имена и элементарные типы данных, к которым они принадлежат.
Пример. Пример структурно-графического определения класса АВТОР изображен на рис. 8.5.
| АВТОР | |
| ID | int |
| Фамилия | string |
| Имя | string |
| Отчество | string |
Рис. 8.5. Определение класса сущностей АВТОР
В этом примере АВТОР – это наименование сущности, в то время как ID, Фамилия, Имя и Отчество являются атрибутами сущности, которым присвоены типы, соответствующие хранимым данным.
Атрибуты – именованные характеристики, отображающие свойства данной сущности.
Пример. Класс сущностей АВТОР описывается атрибутами ID, Фамилия, Имя, Отчество.
В модели «сущность-связь» предполагается, что все экземпляры данного класса сущностей имеют одинаковые атрибуты.
В экземпляре сущности, в отличие от класса, каждый атрибут содержит данные, характеризующие конкретный объект.
Пример. Пример нескольких экземпляров сущности класса АВТОР приведен на рис. 8.6.
| Пушкин | Александр | Сергеевич | |
| Гоголь | Николай | Васильевич |
…
| Чехов | Антон | Павлович |
Рис. 8.6. Несколько экземпляров сущностей класса АВТОР
Как видно из рисунка, все экземпляры имеют одинаковые атрибуты, но разные данные (значения) каждого атрибута.
Идентификаторы (identifiers) – это атрибуты с помощью которых экземпляры именуются, или идентифицируются.
Идентификатор экземпляра сущности состоит из одного или более атрибутов сущности. Идентификатор может быть уникальным (unique) либо неуникальным (nonunique). Если идентификатор является уникальным, его значение будет указывать на один и только на один экземпляр сущности. Если идентификатор является неуникальным, его значение будет указывать на некоторое множество экземпляров. Синонимом термину «идентификатор» является термин «ключ».
Пример. В классе сущностей АВТОР идентификатором является атрибут ID. В случае, если мы в качестве идентификатора приняли бы атрибут Фамилия, этот идентификатор был бы неуникальным. Например, он указывал бы на группу сущностей со значением Толстой у данного атрибута.
Связи (relationships) – это взаимоотношения сущностей.
Модель «сущность-связь» включает в себя классы связей и экземпляры связей. Классы связей определяют взаимоотношения между классами сущностей, а экземпляры связи – взаимоотношения между экземплярами сущностей. У связей могут быть атрибуты.
Класс связей может затрагивать несколько классов сущностей. Число классов сущностей, участвующих в связи, называется степенью связи (relationship degree). Изображенная на рис. 8.7 связь ПРОДАВЕЦ-ЗАКАЗ имеет степень 2, поскольку в ней участвуют два класса сущностей: ПРОДАВЕЦ и ЗАКАЗ. Связь РОДИТЕЛЬ имеет степень 3, так как в ней участвуют три класса сущностей: МАТЬ, ОТЕЦ и РЕБЕНОК. Связи степени 2 весьма распространены, их часто называют еще бинарными связями (hinary relationships).

Рис. 8.7. Типы связей
Типы бинарных связей
На рис. 8.8 показаны три типа бинарных связей.
В связи 1:1 (один к одному) одиночный экземпляр сущности одного типа связан с одиночным экземпляром сущности другого типа. Связь СЛУЖЕБНЫЙ-АВТОМОБИЛЬ связывает одиночную сущность класса СОТРУДНИК с одиночной сущностью класса АВТОМОБИЛЬ. В соответствии с этой диаграммой, ни за одним сотрудником не закреплено более одного автомобиля и ни один автомобиль не закреплен более чем за одним сотрудником.
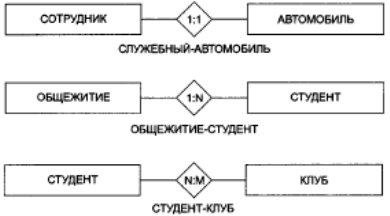
Рис. 8.8. Три типа бинарных связей
В связи типа l: N (один к N, или один ко многим) экземпляр сущности одного типа связан со многими экземплярами сущности другого типа. В нашем примере таким типом связи является связь ОБЩЕЖИТИЕ-СТУДЕНТ, где единичный экземпляр сущности класса ОБЩЕЖИТИЕ связан со многими экземплярами сущности класса СТУДЕНТ, то есть в общежитии может проживать много студентов, но каждый студент живет только в одном общежитии.
Позиции, в которой стоят символы 1 и N, имеют значение. Единица стоит на той стороне связи, где располагается ОБЩЕЖИТИЕ, a N – на той, где располагается СТУДЕНТ Если бы символы 1 и N располагались наоборот (N: 1), получилось бы, что в общежитии живет один студент, причем каждый студент живет в нескольких общежитиях. Это, разумеется, не так.
Третьем типом бинарной связи является связь N:M (читается N к M, или многие ко многим). В нашем примере это связь СТУДЕНТ-КЛУБ, связывающая экземпляры сущностей класса СТУДЕНТ с экземплярами сущностей класса КЛУБ. Один студент может быть членом нескольких клубов, а в одном клубе может состоять много студентов.
Числа внутри ромба, символизирующего связь, обозначают максимальное количество сущностей на каждой стороне связи. Эти ограничения называются максимальными кардинальными числами, а совокупность из двух таких ограничений для обеих сторон связи называется максимальной кардинальностью связи.