Основные методы расчета и определения. Установившиеся и неустановившиеся процессы. Основные принципы подбора типа тел для конкретных процессов.
Понятие установившегося и неустановившегося процессов, особенности передачи тепла теплопроводностью в установившихся и неустановившихся процессах, основные способы управления процессами передачи тепла теплопроводностью при установившихся и неустановившихся процессах, расчеты процессов (постановка задач и их решение). Рассмотреть особенности подбора тел для процессов, где тепло передается теплопроводностью, описать их свойства, особенности расчета и их использование в зависимости от целей (связь с доложенным выше).
Понятие установившегося и неустановившегося процессов
При установившемся (стационарном) процессе температуры в каждой точке аппарата не изменяются во времени, тогда как при неустановившемся (нестационарном) процессе температуры изменяются во времени. Установившиеся процессы соответствуют непрерывной работе аппаратов с постоянным режимом; неустановившиеся процессы протекают в аппаратах периодического действия, а также при пуске и остановке аппаратов непрерывного действия и изменении режима их работы.
Особенности передачи тепла теплопроводностью в установившихся и неустановившихся процессах
Передача тепла теплопроводностью осуществляется путем переноса тепла при непосредственном соприкосновении отдельных частиц тела. При этом энергия передается от одной частицы к другой в результате колебательного движения частиц, без их перемещения друг относительно
Теплопроводность через однослойную плоскую стенку
Рассмотрим передачу тепла теплопроводностью через плоскую стенку, длина и ширина которой намного больше её толщины.
|
|
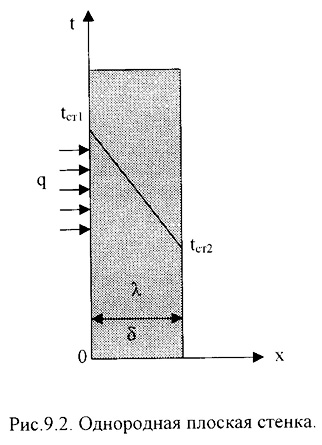
Температуры на поверхностях стенки tст1 и tст2 поддерживаются постоянными, т. е. поверхности являются изотермическими. Температура меняется только в направлении, перпендикулярном плоскости стенки, которое мы принимаем за ось Х. При стационарном режиме температура не меняется во времени, тогда:
Двойное интегрирование:
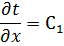
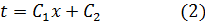
C1 и С2 – константы интегрирования
Зависимость (2) является уравнением прямой линии, т. е. при постоянном коэффициенте теплопроводности закон изменения температуры в однослойной плоской стенке будет линейным.
Константы можно определить из граничных условий:
при х=0 t=tст1, тогда tст1=С2
при х=δ t=tст2, тогда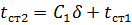 
С1=(tст2- tст1)/δ
Подставим значения констант в (2)
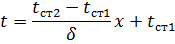
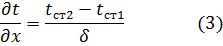
Подставим (3) в уравнение Фурье
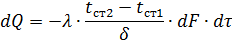
или
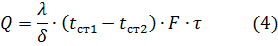
уравнение 4 – уравнение теплопроводности плоской стенки при установившемся процессе теплообмена.
Величина 
- тепловая проводимость, обратная величина – термическое сопротивление стенки (показывает величину падения температуры при прохождении через стенку удельного теплового потока, равного единице).
Теплопроводность через многослойную плоскую стенку
Для многослойной плоской стенки формулу теплопроводности можно вывести из уравнения теплопроводности для каждого отдельного слоя, считая, что тепловой поток, проходящий через эти слои, один и тот же.
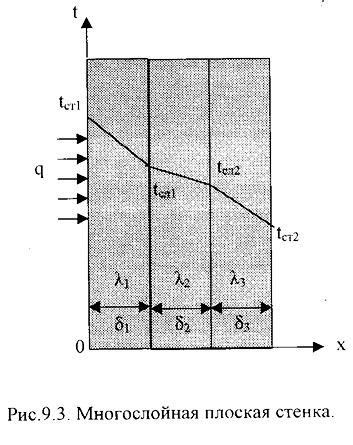
Для каждого слоя можно записать уравнение Фурье как для однослойной плоской стенки:
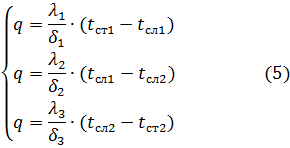
Решая систему получим
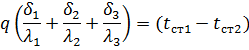
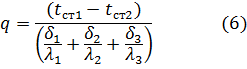
Если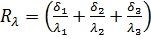 
– термическое сопротивление многослойной плоской стенки, то
|
|
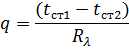
В общем виде для плоской стенки, имеющей n слоёв:
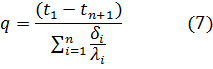
δi и λi – толщина и коэффициент теплопроводности i-го слоя.
Существуют процессы, в которых температура изменяется не только в пространстве, но и во времени. Они делятся на 2 группы: а) тело стремится к тепловому равновесию; б) температура тела претерпевает периодические изменения. К первой группе относятся процессы прогрева или охлаждения тел, помещенных в среду с заданным тепловым состоянием, например, охлаждение металлических брусков. Ко второй группе относятся процессы в периодически действующих подогревателях, например, тепловой процесс регенераторов, насадка которых то нагревается дымовым газами, то охлаждается воздухом.
Нестационарные тепловые процессы всегда связаны с изменением внутренней энергии, или энтальпии, вещества. Передачу теплоты при нестационарном режиме можно определить, если найти закономерности изменения температурного поля и теплового потока в пространстве и во времени:
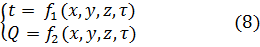
Эти зависимости могут быть найдены из дифференциального уравнения теплопроводности (1):
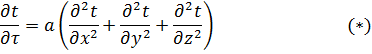
При введении условий для решения диф. уравнения, решением будет следующая зависимость:
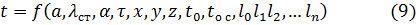
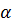- коэффициент теплоотдачи между поверхностью тела и окружающей средой
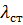- теплопроводность стенки
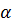- температуропроводность
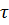- время
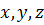- координаты
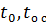- температуры поверхности (в начальный момент времени) и окружающей среды
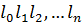- геометрические параметры, характеризуют форму тела
Полученные переменные можно сгруппировать в безразмерные комплексы:
|
|
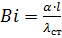- критерий Био (характеризует неравномерность температурного поля)
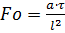– критерий Фурье (характеризует нестационарность процессов)
x/l – безразмерная координата
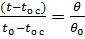– безразмерная температура
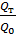– безразмерное количество теплоты
Таким образом,
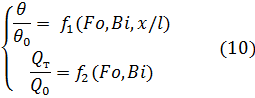
Данные уравнения решаются для конкретной формы тел.
Особенности процесса теплопроводности в зернистом слое с неподвижной газовой (жидкой) фазой
Соотношение, определяющее плотность теплового потока в сплошной среде:
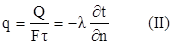
данное уравнение справедливо и для зернистого слоя, если выполняются следующие два условия:
1. Размеры зернистого слоя (отношение диаметров трубы и элемента слоя) должны быть достаточно велики для того, чтобы температурное поле (совокупность значений температур в данный момент времени для всех точек рассматриваемой среды) в нем можно было рассматривать монотонным.
2. Температуры двух фаз (твердой и жидкой или газовой) должны быть тождественны, это выполняется, если если результирующий теплопоток между двумя фазами равен нулю (это не исключает локальный межфазовый теплообмен)
Эти условия в реальном зернистом слое выполняются только приближенно.
Структура зернистого слоя, его порозность и форма должны оказывать значительное влияние на теплопроводность. Предложено много теоретических и экспериментальных зависимостей, определяющих эффективный коэффициент теплопроводности λоэ как функцию структуры слоя и теплопроводности обеих фаз зернистого слоя.
Одной из наиболее простых и физически обоснованных является модель, предложенная Кунии. С учетом всех механизмов переноса теплоты в зернистом слое была получена формула.
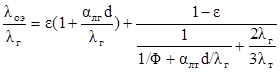
в которой:
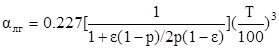
– коэффициент теплоотдачи излучением от зерна через газ мимо соседних зерен
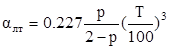
– коэффициент теплоотдачи излучением между соседними зернами;
р - степень черноты поверхности зерен
d – диаметр частицы
Ф - это относительная эффективная толщина газовой прослойки между шарами.
Коэффициент теплопроводности также может быть получен графическим путем. Для пористых материалов на коэф. теплопр-ти влияет внутр.пористстость и средний диаметр пор.