Предварительно следует прочитать п. 1.3. из [1].
Пусть G и D – области на комплексной плоскости. Будем говорить, что задано отображение из G в D ( ), если для всякой точки
), если для всякой точки 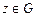 по некоторому правилу или закону поставлена в соответствие точка
по некоторому правилу или закону поставлена в соответствие точка  . Точка
. Точка  называется образом точки
называется образом точки  , а точка
, а точка  - прообразом точки
- прообразом точки  при отображении
при отображении  . Соответственно, если Г и L – кривые в комплексной плоскости, то
. Соответственно, если Г и L – кривые в комплексной плоскости, то  ‑ образ кривой Г, а
‑ образ кривой Г, а  ‑ прообраз кривой L при отображении
‑ прообраз кривой L при отображении  .
.
1.24. а) Найти образы линий  ,
,  ,
,  при отображении
при отображении 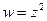 .
.
Можем записать  . Поэтому
. Поэтому 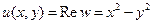 ,
,  . Если
. Если 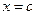 , то получаем в плоскости
, то получаем в плоскости  кривую, заданную параметрически уравнениями
кривую, заданную параметрически уравнениями  ,
,  . Исключая параметр
. Исключая параметр  имеем
имеем  , и, следовательно,
, и, следовательно,  . При каждом фиксированном
. При каждом фиксированном  это парабола с ветвями направленными влево и вершиной в точке
это парабола с ветвями направленными влево и вершиной в точке  и пересекающая мнимую ось при
и пересекающая мнимую ось при  , то есть в точках
, то есть в точках  и
и  . При
. При  получаем отрицательную полуось
получаем отрицательную полуось 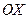 .
.
Если  , то параметрические уравнения образа этой кривой есть
, то параметрические уравнения образа этой кривой есть  ,
,  , откуда, исключая параметр
, откуда, исключая параметр  имеем
имеем  , и, следовательно,
, и, следовательно,  ‑ семейство парабол с ветвями направленными вправо, вершиной в точке
‑ семейство парабол с ветвями направленными вправо, вершиной в точке  и пересекающая мнимую ось при
и пересекающая мнимую ось при  , то есть в точках
, то есть в точках  и
и  . При
. При  получаем положительную полуось
получаем положительную полуось 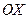 .
.
Если  ,
, 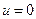 ,
,  , следовательно,
, следовательно,  и образом прямой
и образом прямой  неотрицательная часть мнимой оси.
неотрицательная часть мнимой оси.
б) Найти образы линий  ,
,  ,
,  при отображении при отображении
при отображении при отображении  .
.
Имеем  . Если
. Если 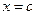 , то
, то  . Это уравнение описывает окружность с центром в начале координат и радиуса
. Это уравнение описывает окружность с центром в начале координат и радиуса  пробегаемую бесконечное число раз. Если
пробегаемую бесконечное число раз. Если  , то
, то  . Это уравнение луча исходящего из начала координат со значением аргумента равным
. Это уравнение луча исходящего из начала координат со значением аргумента равным  . Если
. Если  , то
, то  и мы получаем спираль, описываемую вокруг начала координат.
и мы получаем спираль, описываемую вокруг начала координат.
в) Найти прообразы линий  при отображении
при отображении  .
.
Так как  , то
, то  , если
, если  . При
. При  получаем уравнение
получаем уравнение  , которое описывает пару распадающихся прямых
, которое описывает пару распадающихся прямых  и
и  . При
. При  получаем гиперболы с фокусами на оси
получаем гиперболы с фокусами на оси 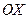 при
при  и фокусами на оси
и фокусами на оси  при
при  и асимптотами
и асимптотами  и
и  . Далее, так как
. Далее, так как  , то
, то  , если
, если  . При
. При  получаем уравнение
получаем уравнение  , которое описывает оси координат. При
, которое описывает оси координат. При  получаем гиперболы лежащие в 1-м и 3-м координатных углах при
получаем гиперболы лежащие в 1-м и 3-м координатных углах при  и гиперболы лежащие во 2-м и 4-м координатных углах при
и гиперболы лежащие во 2-м и 4-м координатных углах при  и асимптотами
и асимптотами  ,
,  . Если
. Если  , то
, то  , или
, или  . Выделяя в последнем уравнении полный квадрат, последовательно имеем
. Выделяя в последнем уравнении полный квадрат, последовательно имеем  ,
,  ,
,  . Это пара распадающихся прямых
. Это пара распадающихся прямых 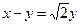 ,
,  , или, что тоже самое
, или, что тоже самое  ,
,  .
.
е) Найти образы линий  и
и  при отображении
при отображении  .
.
Можем записать  . Если
. Если  , то это окружность радиуса
, то это окружность радиуса  пробегаемая два раза. Если
пробегаемая два раза. Если  , то получаем луч исходящий из начала координат под углом
, то получаем луч исходящий из начала координат под углом 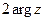 .
.
в) Найти прообразы линий  при отображении
при отображении  .
.
Можем записать  , или
, или  . Если
. Если  , то при
, то при  это половина окружности радиуса
это половина окружности радиуса  лежащая в верхней полуплоскости плоскости
лежащая в верхней полуплоскости плоскости  , при
, при  это половина окружности радиуса
это половина окружности радиуса  лежащая в нижней полуплоскости плоскости
лежащая в нижней полуплоскости плоскости  . Таким образом, прообразом линии
. Таким образом, прообразом линии  при отображении
при отображении  есть окружность радиуса
есть окружность радиуса  пробегаемая бесконечное число раз. Если
пробегаемая бесконечное число раз. Если  , то получаем луч в плоскости
, то получаем луч в плоскости  исходящий из начала координат под углом
исходящий из начала координат под углом  .
.
1.25. Представить в показательной форме а) 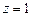 ; б)
; б) 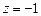 ;
;
в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ;
;
з)  .
.
Имеем а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 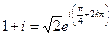 ; е)
; е)  ;
;
ж)  ; з)
; з)  .
.
1.26. Найти модуль, аргумент, вещественную и мнимую части а)  ; б)
; б) 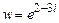 ; в)
; в) 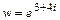 .
.
а) Так как  , то
, то  ,
,  ,
, 
 ;
;
б) Так как 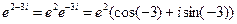 то
то  ,
,  , если главное значение аргумента выбирать из промежутка
, если главное значение аргумента выбирать из промежутка  ,
, 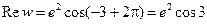 ,
,  ;
;
в) Так как  то
то  ,
,  , если главное значение аргумента выбирать из промежутка
, если главное значение аргумента выбирать из промежутка  потому что
потому что 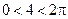 ,
,  ,
,  .
.
1.27. Вычислить а)  ; б)
; б)  ; в)
; в)  .
.
а) 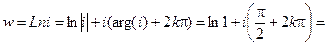
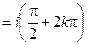 ;
;
б) 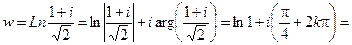
 ;
;
в)  .
.
1.28. Найти вещественную и мнимую части модуль и аргумент комплексного числа 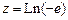 .
.
Имеем
а) 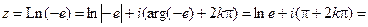
 . Таким образом
. Таким образом  ,
,  ,
,  ,
,  .
.
1.29. Найти вещественную, мнимую части и модуль комплексного числа  .
.
Имеем б)  , откуда
, откуда  . Или
. Или  .
.
Из последнего получаем  . Умножим обе части равенства на
. Умножим обе части равенства на 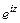 и получим
и получим 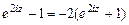 , или
, или  ,
,  . Следовательно
. Следовательно  . Тогда
. Тогда  . Поэтому
. Поэтому  ,
,  ,
,  ,
,
1.30. Решить уравнения: а)  ; б)
; б)  ;
;
а) Так как  , то
, то  . Следовательно,
. Следовательно,  . Умножая обе части равенства на
. Умножая обе части равенства на  получаем
получаем  , откуда
, откуда  . Поэтому
. Поэтому  ;
;
б) Так как  , то
, то  . Следовательно,
. Следовательно,  . Умножая обе части равенства на
. Умножая обе части равенства на  получаем
получаем  . Это квадратное уравнение относительно
. Это квадратное уравнение относительно  . Решая его получаем
. Решая его получаем  или
или  .
.
Из первого соотношения получаем 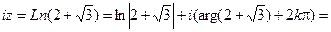
 . Поэтому
. Поэтому  .
.
Из второго соотношения имеем 
 . Поэтому
. Поэтому 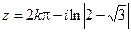 .
.