Квадратурные формулы. Формулы Рунге

Интерполирование функций

Приближенное вычисление определенных интегралов

Постановка задачи

Квадратурные формулы. Формулы Рунге

 

Интерполирование функций

Задача интерполяции – нахождение значения таблично заданной функции в тех точках внутри данного интервала, где она не задана.

Исходные табличные данные могут быть получены экспериментально или расчетным путем по сложным зависимостям.

Решение задачи интерполяции и построение интерполяционной функции L(x), заменяющей исходную f(x), заданную таблично, и проходящей через все заданные точки – узлы интерполяции. С помощью этой функции можно рассчитать искомое значение исходной функции в любой точке (рисунок1).

 

Рисунок 1

 

Метод Лагранжа

Пусть функция y=f(x) определена таблицей:

 

Таблица 1

xi	x0	x1	…	xn
yi	y0	y1	…	yn

 

Значения аргументов { x_i },(i=0,1,…,n) называют узлами интерполяции.

Задачей интерполяции является построение многочлена L(x), значения которого в узлах интерполяции x_i равны соответственно значениям заданной функции:

L(x_i)= y_i,(i=0,1,…,n).

Интерполяционной формулой Лагранжа называется формула, представляющая многочлен L(x) в виде

,

Где 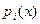- многочлен степени n,принимающий значение, равное единице в узле x_i и нулю в остальных узлах x_k () и принимающий вид:

 

Многочлен L(x) называется интерполяционным многочленом Лагранжа.

Оценить погрешность интерполяции можно по формуле: в точке х из [x₀, x_n]:

, где

- максимальное значение (n+1) производной исходной функции f(x) на отрезке[x₀, x_n].

 

Приближенное вычисление определенных интегралов

Постановка задачи

 

Дана непрерывная функция f(x) на отрезке [a,b]. Требуется вычислить определенный интеграл

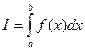
Геометрический смысл определенного интеграла от неотрицательной функции f(x) состоит в том, что значение I- это площадь, ограниченная кривой y= f(x),осью абсцисс и прямыми x=a, x=b (рисунок 2).

a

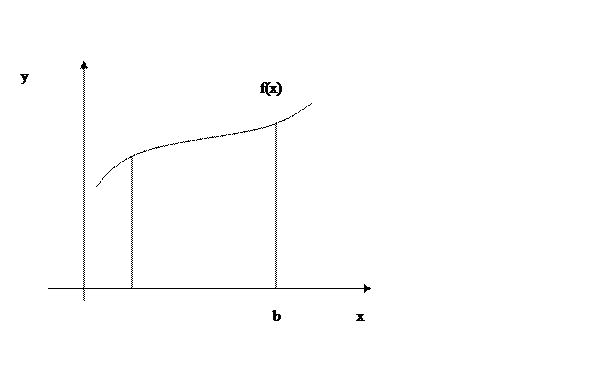
Рисунок 2

Зачастую интеграл не выражается в элементарных функциях. В таких случаях применяется численное интегрирование. Основная идея численного интегрирования заключается в том, что

1. отрезок [a,b] разбивается на n частей [x_i, x_i+1], i=0,1,…,n-1.

2. На каждом частичном отрезке подынтегральная функция заменяется легко интегрируемой функцией.

3. Приближенное значение интеграла I на отрезке [a,b] будет равно сумме интегралов от аппроксимирующей функции на каждом частичном отрезке:

, где

S-квадратурная формула;

R-погрешность квадратурной формулы.

Числа q_i называются весами и зависят от вида квадратурной формулы. Исходная подынтегральная функция вычисляется в узлах z_i, которые также зависят от вида применяемой квадратурной формулы.

 

Квадратурные формулы. Формулы Рунге

 

Сначала рассмотрим квадратурные формулы прямоугольников- левых, правых, средних. Подынтегральная функция заменяется на каждом частичном отрезке прямой, параллельной оси х, т.е. константой , которая легко интегрируется. Получается прямоугольник, площадь которого является приближенным значением интеграла на этом отрезке.

Рисунок 3

 

Если прямая проходит через точку подынтегральной кривой, соответствующей левому узлу отрезка[x_i, x_i+1], то это формула левых прямоугольников-

, (рисунок 3).

через правый узел, то это формула правых прямоугольников

.(рисунок 4)

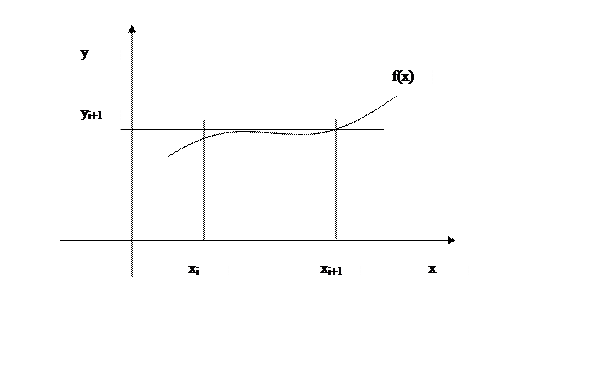
Рисунок 4

 

Если через середину отрезка – то это формула средних прямоугольников –

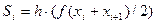.(рисунок 5).

 

Рисунок 5

 

Если подынтегральная функция заменяется прямой, проходящей через точки подынтегральной кривой, соответствующим соседним узлам то получается формула трапеций 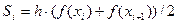.(рисунок 6)

Рисунок 6

 

Просуммировав площади прямоугольников или трапеций на всех частичных отрезках, составляющих отрезок[a,b], получим составные формулы

Правых прямоугольников

Левых прямоугольников

Средних прямоугольников

Трапеций

.

Погрешность квадратурной формулы оценивается величиной остаточного члена R(h), зависящего от шага разбиения h или числа разбиений n.

Для формулы прямоугольников

 

Для формулы трапеций

.

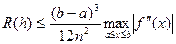Практически используется метод двойного пересчета: По квадратурной формуле проводят вычисление интеграла с шагом и получают значение S(h). Затем уменьшают шаг вдвое и получают новое приближенное значение S(h/2). Чтобы определить, как сильно уклоняется значение S(h/2) от точного значения интеграла, используют правило Рунге:

,

где к=2 для формул прямоугольников и трапеций (порядок точности).

При заданной точности, вычисления с уменьшающимся шагом проводят до тех пор, пока

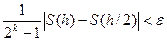. ε-заданная точность.