Сделать краткий конспект. Разобрать и записать все примеры.
Уравнения прямой в пространстве
Канонические уравнения прямой в пространстве
Каноническими уравнениями прямой в пространстве называются уравнения, определяющие прямую, проходящую через заданную точку коллинеарно направляющему вектору.
Пусть дана точка 
и направляющий вектор 
. Произвольная точка 
лежит на прямой l только в том случае, если векторы 
и коллинеарны, т. е. для них выполняется условие:
.
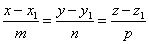Приведённые выше уравнения и есть канонические уравнения прямой.
Числа m, n и p являются проекциями направляющего вектора на координатные оси. Так как вектор 
ненулевой, то все числа m, n и p не могут одновременно равняться нулю. Но одно или два из них могут оказаться равными нулю. В аналитической геометрии допускается, например, такая запись:
,
которая означает, что проекции вектора на оси Oy и Oz равны нулю. Поэтому и вектор 
, и прямая, заданная каноническими уравнениями, перпендикулярны осям Oy и Oz, т. е. плоскости yOz.
Пример 1. Составить уравнения прямой в пространстве, перпендикулярной плоскости 
и проходящей через точку пересечения этой плоскости с осью Oz.
Решение. Найдём точку пересечения данной плоскости с осью Oz. Так как любая точка, лежащая на оси Oz, имеет координаты 
, то, полагая в заданном уравнении плоскости x = y = 0, получим 4 z - 8 = 0 или z = 2. Следовательно, точка пересечения данной плоскости с осью Oz имеет координаты (0; 0; 2). Поскольку искомая прямая перпендикулярна плоскости, она параллельна вектору её нормали 
. Поэтому направляющим вектором прямой может служить вектор нормали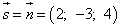 
заданной плоскости.
Теперь запишем искомые уравнения прямой, проходящей через точку A = (0; 0; 2) в направлении вектора 
:
или
.
Уравнения прямой, проходящей через две данные точки
Прямая может быть задана двумя лежащими на ней точками и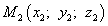 
В этом случае направляющим вектором прямой может служить вектор 
. Тогда канонические уравнения прямой примут вид
.
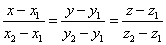Приведённые выше уравнения и определяют прямую, проходящую через две заданные точки.
Пример 2. Составить уравнение прямой в пространстве, проходящей через точки 
и 
.
Решение. Запишем искомые уравнения прямой в виде, приведённом выше в теоретической справке:
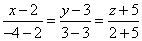
или
.
Так как 
, то искомая прямая перпендикулярна оси Oy.
Прямая как линия пересечения плоскостей
Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей 
и 
, т. е. как множество точек, удовлетворяющих системе двух линейных уравнений
Уравнения системы называются также общими уравнениями прямой в пространстве.
Пример 3. Составить канонические уравнения прямой в пространстве, заданной общими уравнениями
Решение. Чтобы написать канонические уравнения прямой или, что то же самое, уравнения прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой. Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например yOz и xOz.
Точка пересечения прямой с плоскостью yOz имеет абсциссу x = 0. Поэтому, полагая в данной системе уравнений x = 0, получим систему с двумя переменными:
Её решение y = 2, z = 6 вместе с x = 0 определяет точку A (0; 2; 6) искомой прямой. Полагая затем в заданной системе уравнений y = 0, получим систему
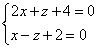
Её решение x = -2, z = 0 вместе с y = 0 определяет точку B (-2; 0; 0) пересечения прямой с плоскостью xOz.
Теперь запишем уравнения прямой, проходящей через точки A (0; 2; 6) и B (-2; 0; 0):
,
или после деления знаменателей на -2:
,
где 
.