Теоретическая часть
Для характеристики тепловых свойств газа, как и всякого другого тела, пользуются особой величиной - теплоемкостью.
Теплоемкостью тела называют количество теплоты, которое нужно подвести к нему или отнять от него для изменения его температуры на 1 К:
.
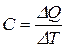Теплоемкость, отнесенная к единице массы вещества, называется удельной теплоемкостью. Она, очевидно, характеризует уже не тело, а вещество, из которого это тело состоит. Теплоемкость, отнесенная к одному молю вещества, называется молярной теплоемкостью.
Между удельной теплоемкостью - c и молярной - C существует очевидное соотношение:
,
где М - молярная масса (измеряется в кг/моль).
Теплоемкость газа зависит от условий его нагревания. В частности, газ можно нагревать при постоянном объеме V или при постоянном давлении Р. Соответственно получаем теплоемкость при постоянном объеме Cv и теплоемкость при постоянном давлении Cp.
Отношение Сp/Сv = γ является параметром при адиабатных процессах и при процессах, близких к ним (γ называют коэффициентом Пуассона).
Процесс называется адиабатным, если в этом процессе нет теплообмена газа с окружающей средой (стенки сосуда теплоизолированы). Если адиабатный процесс является равновесным (в каждый момент времени давление Р и температура Т одинаковы по всему объему), то он описывается уравнением Пуассона
РVγ = const.
Согласно первому началу термодинамики
∆Q = ∆U +∆A,
где ∆Q - количество теплоты, сообщенное газу, ∆U - изменение внутренней энергии газа, ∆A - работа, совершенная газом над внешними телами.
Рассмотрим один моль газа. Если V = const, то ∆A = 0 и, следовательно,
Сv = ∆U / ∆Т. Если Р = const, то ∆A = Р∆V = R ∆T, так как уравнение состояния (PV = RT) справедливо в начальном и конечном состоянии газа.
Следовательно,
.
Таким образом, молярные теплоемкости Cp и Сv для идеального газа связаны соотношением
Cp = Сv + R,
где R - универсальная газовая постоянная.
Cp > Сv, так как при V = const вся сообщаемая газу теплота идет только на изменение внутренней энергии газа, тогда как при Р = const нагревание газа неизбежно сопровождается его расширением. При этом газ совершает работу, для чего приходится сообщать ему дополнительное количество теплоты.
В молекулярно-кинетической теории газов показывается, что 
, где i - число степеней свободы одной молекулы - число независимых координат, с помощью которых однозначно определяется положение и ориентация молекулы в пространстве.
Для одноатомных молекул i = 3 (например, инертные газы), для двух атомной жесткой молекулы (расстояние между молекулами постоянно) i = 5.
Именно такими являются молекулы N2 и О2 в воздухе при комнатных температурах и, следовательно, для них
.
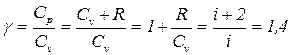Методика определения коэффициента Пуассона
Рассмотрим баллон с воздухом, герметично закрытый поршнем и соединенный с жидкостным U-образным манометром (рис 2.1).
1. Пусть первоначально температура воздуха в баллоне равна комнатной, а давление превышает атмосферное на небольшую величину Р'. Уравнение состояния воздуха в баллоне имеет вид
, (2.1)
где Р - атмосферное давление; Т - абсолютная температура газа, равная температуре окружающей среды; V - объем, занимаемый воздухом; Р' - добавочное давление (определяется по манометру), m - масса воздуха в баллоне, М - молярная масса воздуха (смесь азота и кислорода).
2. Переместим поршень вверх. При этом воздух в баллоне расширяется и охлаждается. Остановим поршень (в положении V2) в тот момент, когда давление в баллоне станет равным атмосферному (уровни жидкости в обоих коленах манометра равны). При расширении газ совершает работу и охлаждается.
После остановки поршня воздух в баллоне нагревается до комнатной температуры (за счет теплообмена с окружающей средой). при этом давление в баллоне повышается на некоторую величину P" (Р" < Р'). Уравнение состояния воздуха в баллоне теперь имеет вид
. (2.2)
Подчеркнем, что масса воздуха в баллоне в состояниях 1 и 2 одинакова.
3. В данной работе существенным является характер перехода воздуха в баллоне из состояния 1 в состояние 2, а именно: если расширение воздуха происходит достаточно быстро, то изменение его внутренней энергии значительно превышает энергию, которая успевает за это время пройти через стенки баллона из окружающей среды, и процесс расширения можно считать адиабатным. Если процесс расширения воздуха в баллоне является равновесным (давление и температура одинаковы по всему объему), то такой процесс описывается уравнением Пуассона: РVγ = const. Ясно, что это справедливо только при медленном расширении. При выполнении обоих из указанных условий уравнение Пуассона применимо и, следовательно,
(Р+P') V1γ =Р V2γ, (2.3)
где P - атмосферное давление.
Из (2.3) находим
, (2.4)
а из (2.1) и (2.2) следует
. (2.5)
Сравнивая (2.4) и (2.5), получаем
. (2.6)
Логарифмируя (2.6), имеем
. (2.7)
При Р' «P (при этом и Р" «P) можно воспользоваться приближением
ln(1 + x)→x при x → 0. [Убедитесь с помощью калькулятора, что при x ≤ 0,02 ошибка при замене ln(1+ x) на x не превышает 1%. А в данной работе h ≈ 0,2 м, тогда как атмосферному давлению соответствует высота водяного столба h ≈ 10 м ].
В результате получаем
, (2.8)
так как Р'=ρgh', Р"=ρgh". Таким образом, измерив h' и h", можно найти коэффициент Пуассона γ.
Описание установки
Экспериментальная установка состоит из металлического баллона, наполненного воздухом, который соединен с манометром и компрессором.
Рис. 2.2. Схема установки:
1 - компрессор, 2 - баллон, 3 - клапан, 4 - U -образный манометр, 5 - вентиль