Индивидуальные контрольные задания.

Колебания.

Вариант 1.

1. Частица совершает прямолинейные гармонические колебания. Максимальная скорость частицы , максимальное ускорение . Найти частоту колебаний ω и амплитуду колебаний А.

2. На поверхности воды вертикально плавает цилиндрическая бутылка. Диаметр бутылки d = 8 см, масса m = 0,5 кг. Если бутылку толчком вывести из положения равновесия, она совершает вертикальные колебания. Найти период колебаний.

3. Частица участвует одновременно в двух колебаниях одного направления: и . Написать уравнение результирующего колебания частицы.

4. Определить коэффициент затухания колебаний математического маятника, если за промежуток времени Δt = 8 мин. маятник теряет 99% своей полной начальной энергии.

5. На горизонтальную мембрану насыпан мелкий песок. Мембрана колеблется с частотой ν = 500 Гц в вертикальном направлении. Определить амплитуду колебаний мембраны, если песчинки подскакивают на высоту h = 3 мм по отношению к положению равновесия мембраны.

6. При какой скорости поезда рессоры вагонов будут колебаться с наибольшей амплитудой под действием толчков колес о стыки рельсов, если длина рельсов 12,5 м, нагрузка на рессору 5,5 т., а рессора прогибается на 16 мм при нагрузке на нее в 1 т.?

7. Во сколько раз амплитуда вынужденных колебаний будет меньше амплитуды при резонансе если частота колебаний будет больше резонансной частоты на 10%, а коэффициент затухания колебаний ( - собственная частота колебаний колебательной системы)?

8. Определить резонансную частоту колебаний в параллельном колебательном контуре, если Ом, Ом, L = 1 мГн, С = 50 мкФ.

Вариант 2.

1. Частица совершает гармонические колебания с периодом Т = 1 с. Найти минимальный промежуток времени, в течение которого смещение частицы меняется от до (А – амплитуда колебаний).

2. На каком расстоянии х от центра масс стержня длины L должна находиться ось колебаний, чтобы такой физический маятник колебался с максимальной частотой? Определить период таких колебаний.

3. Написать уравнение результирующего колебания, образующегося в результате сложения трех однонаправленных колебаний с одинаковым периодом Т = 1 с и равными амплитудами А = 5 см. Начальные фазы колебаний соответственно: . Отобразить решение в виде векторной диаграммы.

4. Масса стержня m, длина L, коэффициент жесткости пружины k. Ось колебаний проходит через конец стержня. Пружина прикреплена к стержню на расстоянии d от оси колебаний. Составить уравнение гармонических колебаний.

Определить период колебаний.

5. Определить логарифмический декремент затухания колебаний математического маятника, если за время t = 1 мин. полная начальная энергия колебаний уменьшается в 10 раз. Длина маятника L = 1 м.

6. Добротность колебательной системы Q = 2, циклическая частота свободных колебаний 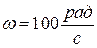. Определить собственную частоту колебаний .

7. Амплитуды вынужденных колебаний при частотах и равны между собой. Определить резонансную частоту колебательной системы.

8. В сеть переменного тока с действующим значением напряжения и частотой ν = 50 Гц включены последовательно емкость С = 20 мкФ, резистор R = 50 Ом и индуктивность L = 0,8 Гн. Определить напряжение на каждом элементе цепи, мощность, выделяющуюся в цепи, угол сдвтга фазы между колебаниями тока и напряжения.

 

Вариант 3.

1. Материальная точка совершает колебания вдоль оси Х по закону , где . Максимальная скорость точки . Определить среднее значение скорости и ускорения точки за промежутки времени и .

2. Написать уравнение результирующего колебания, получающегося в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами Гц, начальными фазами . Амплитуды колебаний см и см. Изобразить траекторию движения точки.

3. Физический маятник представляет собой сплошной диск, колеблющийся в вертикальной плоскости относительно оси, проходящей перпендикулярно плоскости диска. Радиус диска R. На каком расстоянии от центра диска должна проходить ось колебаний, чтобы период колебаний маятника был минимальным?

4. Доска массы M расположена горизонтально и опирается на два вращающихся цилиндра. Расстояние между осями цилиндров d, коэффициент

трения между доской и цилиндрами μ. Если доску сместить из положения равновесия, она будет совершать малые колебания. Показать, что колебания будут гармоническими и найти их период.

5. Амплитуда затухающих колебаний уменьшается в течение одного периода в три раза. На сколько процентов период колебаний больше, чем при отсутствии причины, вызывающей затухание?

6. Амплитуда вынуждающей силы вынужденных колебаний . При этом амплитуда скорости смещений частицы при частотах Гц и 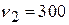Гц оказывается одинаковой. Найти резонансную частоту колебательной системы.

7. Последовательный колебательный контур содержит индуктивность L = 6 мкГн, емкость С = 1 нФ и резистор R = 0,5 Ом. Какую мощность нужно подводить к контуру, чтобы поддерживать в нем незатухающие колебания с амплитудой напряжения на конденсаторе В?

8. Последовательно соединенные резистор R = 100 Ом и конденсатор подключены к источнику переменного тока с действующим значением напряжения В. Действующая сила тока в цепи А. Найти разность фаз колебаний тока и внешнего напряжения, питающего цепь.

 

Вариант 4.

1. Кузов автомобиля установлен на четырех пружинах подвески, на которых может совершать вертикальные колебания. Масса кузова 1460 кг, а частота колебаний 2,95 Гц. Определить частоту колебаний кузова автомобиля, если в нем находятся пять человек средней массой m = 73,2 кг каждый.

2. Плоская платформа участвует в горизонтальных гармонических колебаниях с периодом 2 с. Тело, находящееся на платформе, начинает скользить при амплитуде колебаний А = 0,3 см. Определить коэффициент трения между телом и платформой.

3. Материальная точка участвует одновременно в трех однонаправленных гармонических колебаниях: (см).

С помощью векторной диаграммы найти амплитуду и начальную фазу результирующего колебания. Написать уравнение результирующего колебания.

4. Физический маятник в виде каркаса из жесткой проволоки состоит из дуги полуокружности и прямой (диаметра). Диаметр каркаса d = 50 см. Определить период колебаний в вертикальной плоскости, относительно оси, проходящей через центр окружности.

5. Определить общий путь, пройденный колеблющейся точкой (при колебаниях вперед и назад) до полного затухания колебаний, если начальная амплитуда 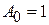мм, логарифмический декремент затухания колебаний θ = 0,0002.

6. Груз массы m = 0,1 кг колеблется на пружине с жесткостью 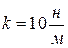. На груз действует внешняя вынуждающая сила с амплитудой Н и частотой в два раза большей собственной частоты колебаний. Коэффициент затухания колебаний . Определить амплитуду колебаний груза. Во сколько раз она будет меньше резонансной амплитуды?

7. В контуре, добротность которого Q = 50 и собственная частота кГц возбуждаются затухающие колебания. Через какое время энергия, запасенная в контуре, уменьшится в два раза?

 

 

8. Внешнее напряжение на источнике тока изменяется гармонически: . Определить силу тока в цепи.

Вариант 5.

1. Материальная точка участвует в гармонических колебаниях с частотой ω. Начальное положение точки , начальная скорость точки . Показать, что смещение точки можно определить уравнением:

.

Если амплитуда колебаний А, показать, что:

,

где а – ускорение, υ – скорость точки.

2. Написать уравнение результирующего колебания, полученное из сложения двух колебаний одного направления и . Найти период биений.

3. Тело массы m подвешено на двух последовательно соединенных пружинах с коэффициентами жесткости и . Определить период колебаний.

4. Материальная точка совершает затухающие колебания с периодом Т = 4,5 с. Начальная амплитуда колебаний мм, а после 20 колебаний амплитуда колебаний А = 1 мм. Определить логарифмический декремент затухания и добротность колебательной системы.

5. Поршень массы m находится в цилиндре, установленном вертикально. В состоянии равновесия расстояние от дна цилиндра до поршня h = 20 см. В цилиндре под поршнем азот. Определить период колебаний поршня, если его вывести из положения равновесия.

 

6. Циклическая частота собственных колебаний в системе , а резонансная частота 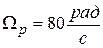. Определить добротность колебательной системы.

7. Цепь питается источником переменного тока с частотой ν = 50 Гц и действующим значением напряжения В. Сопротивление резистора R = 50 Ом, индуктивность L = 0,1 Гн. Показания вольтметров относятся между

собой как . Определить емкость С и действующее значение силы тока.

8. Электрическая цепь состоит из емкости С, индуктивности L и резистора R, включенных параллельно. Цепь питается переменным напряжением . Определить силу тока в цепи и силу тока через каждый элемент цепи.

 

Вариант 6.

1. Маленький упругий мячик падает с высоты h = 3 м на горизонтальную поверхность. Предполагая, что удар абсолютно упругий, показать, что движение будет периодическим. Определить период такого колебательного движения. Будет ли такое колебательное движение гармоническим?

2. Смещение при колебаниях гармонического осциллятора определяется уравнением . Колебания начинаются из положения с начальной скоростью . Определить начальную фазу α и амплитуду колебаний А.

3. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях и . Определить траекторию движения точки.

4. Сплошной диск радиуса R катается без проскальзывания по горизонтальной поверхности под действием упругой пружины, прикрепленной к центру диска. Жесткость

пружины k, масса диска m. Определить период колебаний такого физического маятника.

5. Математический маятник длиной l = 1 м колеблется с амплитудой А = 5 см. Масса маятника m = 0,2 кг. На сколько отличается максимальная сила натяжения нити подвеса маятника от минимальной силы в процессе колебаний?

6. За время t = 100 с маятник совершает n = 200 колебаний. За это время амплитуда колебаний уменьшается в e раз. Определить логарифмический декремент затухания и добротность колебательной системы.

7. Циклическая частота свободных затухающих колебаний в колебательной системе , а резонансная частота . Найти логарифмический декремент затухания и добротность колебательной системы.

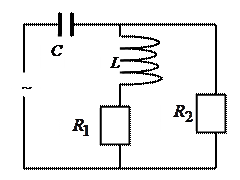
8. Параметры контура, представленного на рисунке, следующие: . Определить резонансную частоту колебаний в контуре.

 

 

Вариант 7.

1. Движение поршня в двигателе внутреннего сгорания можно интерпретировать как гармонические колебания. Определить силу, действующую на коленчатый вал двигателя со стороны поршня, когда он находится в мертвых точках. Масса поршня m = 1,2 кг, коленчатый вал вращается с частотой 2000 об/мин, свободный ход поршня 12 см.

2. Маятниковые часы, период колебаний которых Т = 2 с, на поверхности земли идут точно. На сколько будут отставать эти часы за год, если их переместить на высоту 20 этажа (h = 60 м)? или на высоту h = 1 км?

3. На рисунке изображена траектория движения точки, участвующей в двух взаимно перпендикулярных колебаниях. Написать уравнения колебаний. Частоты колебаний одинаковы и равны ν = 50 Гц.
4. Определить период малых колебаний стержня массы m, длины l относительно оси, проходящей через середину стержня. Коэффициенты жесткости пружин и .

5. Колебательная система с большим затуханием смещается на величину от положения равновесия и затем отпускается, при этом происходят апериодические колебания. Показать, что смещение системы описывается уравнением:

,

где r – коэффициент сопротивления среды, k – коэффициент жесткости пружины,

m – масса колеблющейся точки, , sh и ch – соответственно гиперболический синус и косинус.

6. В течение некоторого промежутка времени маятник совершает 100 колебаний, и амплитуда колебаний уменьшается при этом в 5 раз. Определить добротность колебательной системы.

7. Циклическая частота свободных затухающих колебаний в некоторой колебательной системе , а резонансная частота . Найти логарифмический декремент затухания и добротность колебательной системы.

8. В последовательном колебательном контуре, в котором поддерживаются вынужденные электрические колебания с амплитудой , амплитуды напряжения на индуктивности В, на емкости В, на резисторе В. Определить величину напряжения и угол сдвига фазы между колебаниями тока и напряжения.

 

Вариант 8.

1. Частица колеблется по закону (см). Определить путь, пройденный частицей за один период колебаний Т. Найти среднюю скорость частицы за промежуток времени .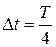

2. Написать уравнение результирующего колебания, полученного при сложении

трех колебаний одного направления: .

3. Математический маятник колеблется по закону: (φ – угол отклонения от положения равновесия). Масса маятника m, длина нити подвеса l. По какому закону изменяется со временем сила натяжения нити подвеса?

4. Предположим, что Земля просверлена по диаметру так, что образовался канал. В образовавшуюся шахту без начальной скорости опускается тело массы m. Показать, что движение тела происходит по закону гармонических колебаний.

Определить период таких колебаний, приняв Землю за однородный шар с плотностью .

5. Через какое время энергия колебаний камертона с частотой ν = 600 Гц уменьшается в миллион раз, если логарифмический декремент затухания колебаний θ = 0,0008?

6. Под действием вынуждающей силы колебательная система совершает установившиеся колебания, описываемые функцией . Найти работу вынуждающей силы за один период колебаний.

7. Добротность колебательной системы Q = 2. Определить отношение амплитуды вынужденных колебаний при частоте вынуждающей силы равной собственной частоте колебаний системы к амплитуде при резонансе.

8. Последовательный колебательный контур состоит из индуктивности L = 0,1 мГн, конденсатора С = 0,01 мкФ и резистора R =3 Ом. Определить среднюю мощность, потребляемую контуром, необходимую для поддержания в нем колебаний с амплитудой напряжения на конденсаторе В.

 

Вариант 9.

1. Материальная точка совершает гармонические колебания. При смещении точки от положения равновесия на см ее скорость , а при смещении на см скорость . Найти частоту и амплитуду колебаний.

2. Результирующее колебание точки, образующееся в результате суперпозиции двух колебаний, описывается уравнением: . Определить частоты складываемых колебаний. Изобразить графически результат сложения. Определить период биений.

3. Сплошной диск радиуса R и массы m подвешен на упругой нити в центре диска. Определить период малых крутильных колебаний диска. Считать нить упругой, для которой момент силы М, создающей угол поворота, пропорционален самому углу поворота: М = γφ.

4. Тело массы m = 12 г участвует в затухающих колебаниях с частотой ν = 1 Гц. За время Δt = 1 мин полная энергия колебаний тела уменьшается на 90%. Определить логарифмический декремент затухания и добротность колебательной системы.

5. Добротность колебательной системы Q = 2, циклическая частота свободных колебаний . Определить собственную частоту колебаний системы.

6. Колебания осциллятора определяются уравнением , а вынуждающая сила, действующая на него, изменяется по уравнению . Масса осциллятора m. Определить коэффициент затухания колебаний.

7. Последовательный колебательный контур питается напряжением В Найти напряжение на сопротивлении , если известно, что напряжение на емкости и напряжение на индуктивности .

8. В цепи действует источник переменного напряжения . Показать, что при выполнении условия 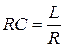ток в цепи не зависит от значения циклической частоты Ω.

~ R R C L

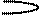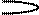
Вариант 10.

1. Частица участвует в гармонических колебаниях, определяемых уравнением 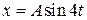(см). В некоторый момент времени смещение частицы см и ее скорость . Найти смещение и скорость частицы через промежуток времени Δt = 2,4 с после этого момента.

2. Материальная точка участвует одновременно в двух колебаниях, взаимно перпендикулярных по направлению: 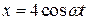и . Определить траекторию движения точки.

3. Тонкая прямоугольная пластина колеблется относительно горизонтальной оси, лежащей в ее плоскости и перпендикулярной к одной из ее сторон, длина которой l. При каком расстоянии х оси от верхней кромки пластины период колебаний будет минимальным?

4. Диск диаметром D = 10 см подвешен на тонком стержне длиной l = 10 см. Определить относительную погрешность, которая допускается, если при вычислении периода колебаний его принимают за математический маятник длиной см. Массой стержня пренебречь.

5. Тело массы m = 360 г, подвешенное на пружине, совершает затухающие колебания. Коэффициент жесткости пружины . Логарифмический декремент затухания системы θ = 0,001. Сколько колебаний происходит в системе, при уменьшении амплитуды колебаний в e раз? За какой промежуток времени это произойдет?

6. Амплитуда скорости вынужденных колебаний материальной точки при частотах вынуждающей силы Гц и 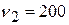Гц равны между собой. Найти резонансную частоту колебательной системы.

7. На последовательный колебательный контур подается переменное напряжение с амплитудой . Показать, что при резонансе тока напряжение на конденсаторе (Q – добротность контура).

 

 

8. В колебательном контуре с параметрами: L = 0,01 Гн, С = 10 мкФ, Ом, Ом возбуждаются незатухающие вынужденные колебания. Определить резонансную частоту этих вынужденных колебаний.

~

 

Вариант 11.

1. Циклическая частота свободных незатухающих колебаний материальной точки . Определить наименьший промежуток времени, за который потенциальная энергия колебаний уменьшается в два раза по сравнению со своим наибольшим значением.

2. Математический маятник длиной l совершает колебания вблизи вертикальной стены. Под точкой подвеса маятника на расстоянии в стену вбит гвоздь. Найти период колебаний маятника.

3. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях: 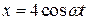и . Построить траекторию движения точки.

4. К пружине с коэффициентом жесткости k подвешено тело массы m. Как известно период колебаний такого пружинного маятника . Затем пружина перерезается пополам и к ее половине подвешивается то же тело. Найти период колебаний полученного осциллятора, сравнить его с периодом Т.

5. Коэффициент затухания при колебаниях осциллятора достаточно мал. Если осциллятор начинает колебаться в момент времени t = 0 со скоростью υ, то через время равное периоду колебаний t = T его скорость 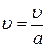(а > 0). Какой будет скорость тела в момент времени ?

6. Монокристалл кварца, применяющийся в генераторах тактовой частоты, можно рассматривать как колебательную систему с добротностью и собственной частотой колебаний . Оценить время, за которое в кристалле устанавливаются вынужденные колебания.

7. Человек находится вблизи вторичной обмотки высоковольтного трансформатора. Частота колебаний напряжения ν = 50 Гц, напряжение на первичной обмотке коэффициент трансформации 22,7. Сопротивление тела человека R = 50 кОм, электрическая емкость связи человека и

~

вторичной обмоткой трансформатора С = 20 пкФ. Определить напряжение под действием которого находится человек.

8. Катушка индуктивности, сопротивление которой R = 12 Ом, включена в цепь переменного тока с частотой ν = 50 Гц. Сдвиг фазы между колебаниями тока и напряжения на катушке . Определить индуктивность катушки.

 

Вариант 12.

1. Материальная точка колеблется в соответствии с уравнением (см). Найти среднее значение скорости частицы за промежуток времени равный: 1)периоду колебаний Т; 2) за первую часть периода Т; 3) за вторую часть периода колебаний Т.

 

 

2. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях

и . Определить траекторию движения точки.

3. Стержень длины l и массы m колеблется под действием двух пружин с коэффициентами жесткости , закрепленными за его конец. Определить период малых колебаний стержня.

4. Циклическая частота свободных колебаний некоторой системы , резонансная частота . Определить добротность колебательной системы..

5. Математический маятник совершает затухающие колебания в среде с логарифмическим декрементом затухания . Определить декремент затухания в случае, если сопротивление среды увеличится в два раза.

6. Механическая колебательная система характеризуется логарифмическим декрементом затухания θ = 1,57. Под действием внешней гармонической силы система участвует в вынужденных колебаниях. Найти отношение резонансной амплитуды к амплитуде при малых частотах колебаний.

7. Последовательный колебательный контур с емкостью С = 1,1 нФ и индуктивностью L = 5 мГн характеризуется логарифмическим декрементом затухания κ = 0,005. Определить время, в течение которого в контуре происходит потеря 99% начальной энергии колебаний в контуре.

8. Определить резонансную частоту колебаний в контуре с параметрами .

 

Вариант 13.

1. Материальная точки участвует в колебаниях в соответствии с уравнением (м). Определить среднюю скорость точки 1) за период колебаний Т,

2) за первую четверть периода, 3) за вторую четверть периода.

2. Точка участвует в двух взаимно перпендикулярных колебаниях. Траектории точки представляет собой эллипс. Написать уравнение колебаний точки вдоль каждой оси координат.

x

3. Потенциальная энергия частицы массы m, находящейся в центрально симметричном силовом поле имеет вид:

(a, b – const)

Определить частоту малых колебаний частицы относительно положения равновесия в радиальном направлении.

4. Механическая система, имеющая собственную частоту колебаний , в условиях колебаний в среде с малой вязкостью колеблется с частотой . Определить добротность колебательной системы.

5. Тело массы m = 20 г подвешено на пружине с коэффициентом жесткости 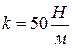и совершает вынужденные колебания под действием гармонической силы. При резонансной частоте Гц амплитуда колебаний см. Определить амплитуду вынуждающей силы и добротность колебательной системы.

6. В колебательной системе с добротностью Q = 5 происходят затухающие колебания с частотой 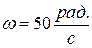. Под действием внешней гармонической силы в системе устанавливаются вынужденные колебания, отстающие по фазе от колебаний вынуждающей силы на . Определить частоту колебаний вынуждающей силы Ω.

7. Последовательный колебательный контур, содержащий все элементы цепи

R,L,C подключен к источнику переменного напряжения . При частотах