Приближение Борна-Оппенгеймера. Адиабатическое приближение. Неадибатическое решение стационарного уравнения Шредингера. Границы применимости адиабатического приближения.
Оба эти приближения основаны на том, что масса ядер примерно в тысячи раз больше массы электрона. Электроны движутся с высокой скоростью около 1% от скорости света. Поэтому можно считать, что электрон движется в поле покоящихся ядер. В этом заключается смысл приближений. (формулы лекций). Допустим, известно решение электронного уравнения Шредингера.
параметры задаются до начала решения уравнения. Поскольку оператор Гамильтона эрмитов, то мы выбираем решение электронного уравнения Шредингера ввиде ортонормированных электронноволновых функций.
(формулки тут всякие) для того, чтобы упростить полученные уравнения мы используем свойство ортонормальности электроноволновых функций.
Переходим к интегралам умножая слева на житую электронную функцию и интегрируем…(еще куча формулок) Приближение Борна-Оппенгеймера заключается в приближении элементами не адиабатического приближения 1,2 порядка. (формулки) Не адиабатические элементы ответственны за преобразование типа электронноволновой функции при изменении ядерных координат. Адиабатическое приближение и приближение Оппенгеймера не применимо в том случае, если при изменении ядерной конфигурации меняется тип конфигурации. Ядерные параметры становятся переменными. В адиабатическом приближении остается 1 не адиабатический элемент 2 порядка для i=j. Этот вклад называется диогональной коллекцией (формулка). Чаще всего приближение Борна – Оппенгеймера не применимо к фотохимическим реакциям и иногда не применимо к реакциям сопровождающимся гомолитическими разрывами связи. (реакция)
молекула LiF полярна и описывается ввиде 2 суперпозиций 2-х волновых функций полярной и неполярной. Энергия полярной меньше энергии неполярной, но полярная молекула диссоциирует на атомы.
Изолированные атомы устойчивее ионов. Для разделенных Liи F энергия ионноволновой функции больше чем энергия неполярной волновой функции.
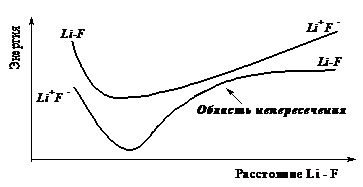
Р и с. 3.2. Кривые диссоциации молекулы Li-F
В области пересечения приближения Оппенгеймера неприменимо. После принятия приближения Борна – Оппенгеймера молекулярное уравнение Шредингера распадается на 2 уравнения (формулки).
Сначало решают электронное уравнение Шредингера при заданных координатах ядер. Координаты ядер можно задать 2 способами. Далее оптимизируют геометрию с целью поиска минимума эл. Энергии.
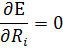
Далее решают ядерное уравнение Шредингера. Из найденной ядерно-волновой функции вычисляются колебательные и вращательные уровни Е.
Эти результаты помогают вычислить ИК спектры, микроволновые спектры, комбинационно рассеянные (Романовские).
Решение ядерного уравнения позволяет вычислить энергию нулевых колебаний ядер, а также энергию колебательную, поступательную и вращательную движения молекулы в целом. Эти 4 вклада необходимы для вычисления энергетического характера молекул при стандартных условиях.
Классификация движений молекул позволяет вычислить как энтропию, так и энтальпию энергетических молекул. Зная энтропию, можно узнать энегрия Гиббса. Е эл. (типа стрелочка вправо) ΔЕ, G°(тоже стрелка) ΔG°.
ΔЕ практически ΔG°
14. Орбитальная модель. Электронный оператор Гамильтона. Одноэлектронный гамильтониан и оператор электронного отталкивания. Понятия "орбиталь", "спин-орбиталь". Спин-орбитальный детерминант (детерминант Слэйтера). Полная формулировка орбитальной модели.
Орбитальная модель –графическое изображение распределения плотности заряда электрона в атоме… Обоснование орбитальной модели атома, исходящее из корпускулярного характера электрона, состоит в следующем. Вероятность определенного положения электрона внутри объема пространства, окружающего атомное ядро, весьма велика, так как рассматривается устойчивое (реально существующее) состояние атома. Такое распределение следует понимать так, что на любом выбранном расстоянии от ядра вероятность пребывания электрона одинакова во всех направлениях радиуса-вектора. Как следует из рис. 9, вероятность пребывания электрона в атомном ядре равна нулю, она незначительна вблизи ядра, но быстро возрастает при удалении от ядра. На некотором расстоянии (для атома водорода оно равно. Бора) вероятность достигает максимума, а затем, медленно уменьшается, асимптотически приближаясь к нулю на расстоянии, стремящемся к бесконечности
Электронный оператор Гамильтона -(Оператор набла ∇)– это символический вектор, сочетающий в себе векторные и дифференцирующие свойства.
,
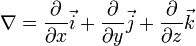Более близкие к истинным решения получают с помощью метода самосогласованного поля (ССП), предложенного Хартри. В методеССП межэлектронным отталкиванием не пренебрегают, но действие на данный электрон всех остальных электронов заменяют средним полем, приближенно воспроизводящим их суммарное действие; последнее зависит от координат только рассматриваемого электрона. Это дает возможность разделить в сферической системе координат переменные в уравнении Шредингера. С формальной точки зрения это достигается следующим образом. Одноэлектронный гамильтониан записывают в виде:https://quant.distant.ru/files/Atom/Atom_razd.pdf (со стр 8 формулы)
Последнее слагаемое описывает отталкивание между электронами i и j, усредненное по всем положениям электрона j и, следовательно, зависящее только от координат электрона i. Последствия этого состоят в следующем.
Рассмотрим гамильтониан(формула)
Его собственные функции (функции Хартри) имеют вид орбитальных произведений:(формула)
Собственные значения Н представляются суммой собственных значенийh iССП: (опять долбанная формула)
Энергия εi есть сумма кинетической энергии i-го электрона, потенциальной энергии его притяжения к ядру и средней потенциальной энергии его отталкивания от остальных электронов. Следовательно, Е` есть сумма кинетической энергии всех электронов, потенциальной энергии их притяжения к ядру и удвоенной потенциальной энергии их усредненного отталкивания от остальных электронов. Удвоение возникло потому, что отталкивание между электронами i и j учтено дважды: как среднее по j в hiССП и среднее по i в hjССП. С учетом этого, полная энергия атома равна: (формулы) Соответственно, гамильтониан атома должен иметь вид: (формулы) Таким образом, необходимо решить систему одноэлектронных уравнений с гамильтонианом (45), включающим усредненное межэлектронное взаимодействие – системууравнений Хартри. Для этого нужно построить набор операторов hiССП для чего следует прежде рассчитать усредненные величины (формул). Значит, отталкивание электрона i, усредненное по всем положениям электрона j, равно: (формула)
Однако, чтобы вычислить этот интеграл, волновые функции χ j (rj)должны уже быть известны! Этопротиворечие преодолевается следующим образом. Сначала задаются некоторым набором N одноэлектронныхфункций, максимально близких к правильным χ j0(rj) (позже мы увидим, что сделать это легко). С их помощью вычисляют интеграл (46) и строят оператор (hi0)ССП. Затем решают набор одноэлектронных уравнений Хартри, возникающий из условия минимума среднего значения гамильтониана (40), вычисляемого с волновой функцией Хартри (42): (формула)
Полученные решенияχ j1(rj)используют, чтобы построить "исправленный" оператор(hi1)ССП, вновь решают ту же систему уравнений, но теперь – с(hi1)ССПи т.д. – до тех пор, пока получаемые собственныезначения уравнений Хартри (т.е. энергии состояний)будут отличаться от полученных на предыдущей итерации лишь на очень незначительную величину (~ 10-6 а.е.)Этот процесс называется самосогласованием, а результирующее поле, создающее усредненный потенциал в (40), называется самосогласованным полем – отсюда и название метода. (хз то ли вообще, другого не нашла)
ОРБИТАЛЬ – область наиболее вероятного местонахождения электрона в атоме (атомная орбиталь) или в молекуле (молекулярная орбиталь).
Спин-орбиталь — это одноэлектронная волновая функция, получаемая из орбитали умножением ее на «спин-функцию», описывающую спиновое состояние отдельного электрона.
Детерминант Слейтера – детерминант, построенный из ортонормированных спин-орбиталей - атомных или молекулярных. Позволяет получить приближенную многоэлектронную волновую функцию N электронов, обеспечивая ее правильные антисимметричные свойства. Элементы детерминанта Слейтера есть описывающие электроны орбитали и перестановка электронов эквивалентна перестановке местами столбцов (строк) детерминанта, что изменяет его знак:
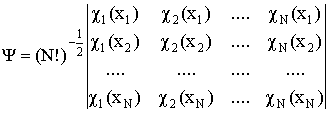
Детерминант Слейтера является единственной функцией, обеспечивающей антисимметричность волновой функции, записанной через орбитали (орбитальное приближение). Следовательно, он дает только одно решение соответствующих одноэлектронных уравнений. Хотя электроны неразличимы, в орбитальном приближении каждый электрон описывается "своей" волновой функцией. Системы, в которых все электроны занимают орбитали попарно, называются системами с закрытыми (замкнутыми) электронными оболочками. Для таких систем детерминант Слейтера состоит из дважды занятых электронами орбиталей, число которых равно половине числа электронов. Системы с нечетнымчислом электронов называются системами с открытыми (незамкнутыми) оболочками.
Наиболее полная формулировка орбитальной модели такова:
волновая функция многоэлектронной системы может быть представлена ввиде линейной комбинации функций Фk(k=1,2,…М)
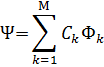
Каждая функция Фkособым образом построена из множества (набора) спин-орбиталей ψ(r, ϭ). Каждая из спин-орбиталей представляет из себя произведение: ψ(r, ϭ)=φ(r) * η(ϭ).
Одной из орбиталей φ(r), входящих в исходный набор ортонормированных функций φi(r), i=1,2…,К., и одной из двух ортонормированных спиновых функций ηi(ϭ), i=1,2.
Применение вариационного принципа для оптимизации волновой функции орбитальной модели. Линейный вариационный метод (метод Ритца). Вековое (секулярное) уравнение. Гамильтонова матрица.
Решением дифференциального уравнения Шрёдингера является волновая функция, и для ее поиска используется вариационный принцип, основанный на следующей теореме:
Пусть самое низкое собственное значение оператора Гамильтона для исследуемой системы равно Е1, а Ψ1 – точная волновая функция, соответствующая этому собственному значению. То есть точная функция Ψ1 определяет основное состояние системы с энергией Е1. В этом случае для любой произвольной нормированной функции Ψ выполняется условие:
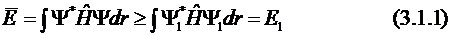
(условимся, что r – набор координат всех рассматриваемых частиц, а знак интеграла – многомерный интеграл с пределами интегрирования по всему пространству: от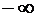 
до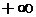 
).
Согласно вариационному принципу, энергия любой пробной функции будет не меньше энергии точной функции. Действительно, произвольная функция Ψ может быть представлена в виде разложения в ряд по собственным функциям оператора Гамильтона:
Будем считать эти функции ортонормированными (здесь δij – символ Кронекера):
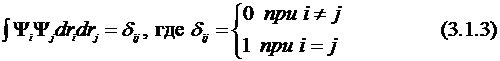
Если функция Ψ нормирована, то
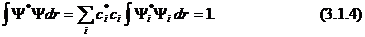
Отсюда следует, что
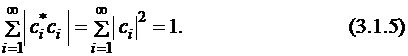
Подставим разложение неизвестной функции по собственным функциям (3.1.2) в уравнение для средней энергии (см. постулат 5) (будем считать для простоты все функции и коэффициенты ci действительными):
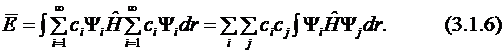
Здесь интеграл отличен от 0 только при равных i и j, т.к. функции ортогональны (3.1.3). С учётом того, что
получаем:
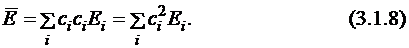
Теперь надо показать, что разность между средней энергией (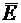
) и энергией основного состояния (
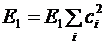) больше или равна нулю:
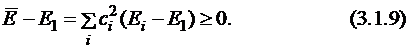
Действительно, выражение под знаком суммы всегда положительно или равно нулю, т.к.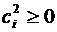 
и Ei всегда больше энергии основного состояния.
Приближённая функция Ψ называется пробной волновой функцией. Чем лучше пробная функция аппроксимирует точную, тем ближе вычисленное значение энергии к точному. При этом вычисленное значение всегда будет не меньше точного.
Коэффициенты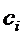 
находят из условия минимума энергии, т.е. равенства нулю производных энергии по коэффициентам:
Однако в действительности полный набор собственных функций оператора Гамильтона неизвестен. Найти полный набор невозможно хотя бы потому, что он бесконечен. Поэтому Ритц предложил использовать пробную волновую функцию в виде линейной комбинации некоторых независимых функций. При этом число этих функций конечно и равно n, а сами функции не являются ортонормированными:
где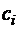 
– варьируемые параметры, которые определяют пробную волновую функцию и которые нужно найти. Подставляем эту сумму в выражение для полной энергии (см. 5-й постулат):
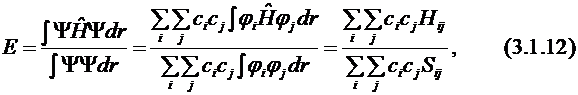
где Hij и Sij – матричные элементы оператора Гамильтона и матрицы перекрывания соответственно (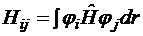
, 
).
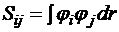Перепишем уравнение в другом виде и продифференцируем его по коэффициентам :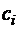
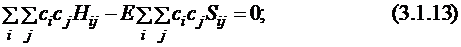
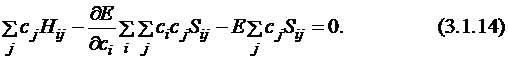
Так как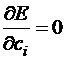 
, то получаем:
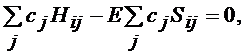(3.1.15)
или
Полученная система однородных линейных уравнений имеет нетривиальное решение только тогда, когда её детерминант равен нулю:
Уравнения (3.1.16) называются секулярными, или вековыми. При решении системы уравнений (3.1.16) находят корни Е 1, Е 2, …, En. Наименьший корень соответствует энергии основного состояния, остальные – энергиям возбуждённых состояний. Для нахождения функции основного состояния необходимо подставить в систему уравнений найденное значение Е 1 и найти коэффициенты .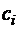
Решение уравнения Шрёдингера для молекулы водорода, для гомоядерных и гетероядерных двухатомных молекул. Молекулярные термы.
Электронные состояния атомов нумеруют с помощью квантового числа L, задающего квадрат суммарного углового момента электронов. В отсутствии внешних полей все направления равноправны, и состояния с разными проекциями момента на ось z (напомним, что таких состояний ровно 2L+1) имеют одинаковую энергию. В результате энергетические уровни 2L+1-кратно вырождены. Обычно значения L задают буквами, как в атоме водорода, где состояния обозначаются как s, p, d… при значениях квантового числа l, описывающих угловой момент электрона, 0, 1, 2,... соответственно. Как принято в квантовой механике, для состояний многоэлектронных систем используются заглавные буквы: состояниям с L = 0, 1, 2,.. соответствуют символы S, P, D,…латинского алфавита.
Атом обладает очень высокой сферической симметрией и классификация состояний по угловому моменту – это классификация по типам симметрии относительно всевозможных поворотов. Кроме поворотов группа симметрии атома включает инверсию. При инверсии волновая функция может либо сохранять, либо менять знак, т.е. состояния обладают определенной четностью. Четность указывают не всегда, причем раньше её указывали нижними индексами g или u (от немецких слов gerade и ungerade), а потом стали использовать верхние индексы "o" (от английского слова odd) для указания только нечетных состояний. В верхнем левом углу символа состояния указывают спиновую мультиплетность – число 2S+1. Принято называть состояния с заданной мультиплетностью 2S+1 синглетными (S = 0, 2S+1 = 1), триплетными (S = 1, 2S+1 = 3), квинтетными (S = 1, 2S+1 = 3) и т.д. (при четном числе электронов в атоме и, следовательно, целом значении S) и дублетными (S = 1/2, 2S+1 = 2), квартетными (S = 3/2, 2S+1 = 4), секстетными (S = 5/2, 2S+1 = 6),...(при нечетном числе электронов). Состояние атома с данными L и S вырождено (2S+1)×(2L+1) раз.
Например, низшие по энергии состояния атома азота – это 4So, 2Do, 2Po, 4P, 2P,... Cимвол состояния 2Do, например, произносится так: "нечетное дублетное D-состояние". Это состояние имеет кратность вырождения 2×(2×2+1) = 10, а четное квартетное Р-состояние (4P) – 4×3 = 12.
При заметном спин-орбитальном взаимодействии имеет смысл лишь суммарныйэлектронный момент J = L+S. Число J, нумерующее собственные значения квадрата суммарного момента указывают обычно справа внизу символа состояния. Такое состояние вырождено 2J+1 раз.Для тяжелых атомов иногда указывают только J (цифрой) и чётность состояния. Индексы i и r, используемые иногда в символах состояний, указывают на заполнение валентной оболочки больше, или меньше чем на половину. Одну и ту же конфигурацию, например, 1s22s22p2имеют принципиально разные электронные состояния 3P0, 3P1, 3P2, 1D2, 1S0 (приведены в порядке возрастания энергии, определяемом иногда правилами Гунда) атома С. Электронные термы этих состояний составляют соответственно 0, 16.40, 43.40, 10192.63, 21648,01 см-1 (терм низшего по энергии, основного состояния по традиции принимается равным нулю). Напомним также, что задание волновой функции электронной конфигурацией имеет смысл лишь в контексте приближенных методов типа Хартри–Фока или функционала плотности.
Двухатомная молекула обладает довольно высокой симметрией. Два ядра лежат на оси z и задают аксиально-симметричный потенциал, в котором движутся электроны. Группа симметрии ядерной конфигурации включает операции поворотов вокруг осисимметрии С ∞ и отражения в любых плоскостях симметрии σv, содержащих эту ось. Такая группа симметрии – С ∞v – соответствует гетероядерным молекулам. В случае гомоядерных молекул имеется ещё центр инверсии i, а также другие элементы симметрии, вызванные наличием i: любые оси симметрии второго порядка, проходящие через центр и перпендикулярные оси z, а также плоскость симметрии σh, перпендикулярная оси z. Эти молекулыотносятся к группе симметрии D∞h. Осевая симметрия позволяет классифицировать электронные состояния с помощью оператора проекции суммарного электронного углового момента Lz. Собственные значения этого оператора задаются числами hLz (Lz =0, ±1,...) и, с классической точки зрения, описывают вращение электронов вокруг оси z. Поскольку вращению по- и против часовой стрелки должна отвечать одинаковая энергия, энергии состояний с одинаковыми значениями Λ=|Lz|, но разными знаками Lz, должны совпадать, т.е. эти состояния двукратно вырождены (если не принимается во внимание спин-орбитальное взаимодействие). Электронные состояния двухатомных молекул классифицируются по значениям квантовых чисел Λ и чисел, описывающих квадрат спина (S) и проекцию спина на ось z (Σ). При этом используют буквенные обозначения, похожие на обозначения состояний с разным угловым моментом для атомов. Если описывают симметрию волновых функций одноэлектронных состояний (т.е. орбиталей) с Λ = 0, 1, 2, 3,…, используют буквыгреческого алфавита: σ, π, δ, ϕ… Для многоэлектронных систем используются заглавныебуквы: Σ, Π, Δ, Φ...
Примечание: Соответствие s – σ, p – π, d – δ, f – Φ очевидно, но далее символы следуют в соответствии с греческим алфавитом: при Λ = 4, например, орбитали имеют тип ψ, а многоэлектронные функции – Ψ. В случае Σ-состояний возможно различие в волновых функции относительно отражения в плоскости σv: волновые функции состояний типа Σ+ не изменяются, а в случае состояний Σ– меняют знак на противоположный (для орбиталей в трехмерном пространстве эту четность не указывают, так как нельзя построить ненулевую орбиталь σ–типа). При Λ > 0 операции отражения σv соответствует уже рассмотренное изменение направления вращения. Для гомоядерных систем надо еще указать, меняет или не меняет знак функция при инверсии. Нечетные и четные функции обозначают нижними правыми индексами u или g соответственно. В верхнем левом углу символа состояния указывают спиновую мультиплетность – число 2S+1. Основное, самое нижнее по энергии электронное состояние обозначается буквой Х, следующие по энергии – заглавными буквами латинского алфавита А, В, С…, если состояния имеют ту же мультиплетность 2S+1, что и основное, или малыми буквами a, b, c,…, если они отличаются по спину; иногда используют штрихи при буквенных символах. Отметим, что в этой номенклатуре есть и исторически сложившиеся исключения. Дело в том, что нумерация электронных состояний "по имени" складывалась в том порядке, в котором эти состояния открывались (чаще всего в этих случаях используются символы состояния со штрихами).
Вырождение состояний с разными проекциями спина происходит, лишь, если в молекуле отсутствует или очень мало спин-орбитальное взаимодействие. Если оно велико, (что типично для молекул с тяжелыми ядрами), то электронное состояние молекулы характеризуется не только числом Λ, но и числом Ω, равным модулю проекции суммарного электронного момента импульса на ось: Ω=|Lz+Σ|. Например, для состояния типа 2Π возможные значения Ω могут быть равны 3/2 (при Lz =1, Σ = +1/2, или при Lz = –1, Σ = –1/2) и 1/2 (при Lz =1, Σ = –1/2 или при Lz = –1, Σ = +1/2). Такие состояния обозначают дополнительным символом Ω в правом нижнем углу (или в скобках).
Среднее значение электронного гамильтониана в электронном состоянии Ψn – это электронная энергия En. Она то и играет роль потенциальной энергии при изучении движений ядер с помощью ядерного уравнения Шредингера. Для двухатомной молекулы это уравнение можно записать так: (формула)
https://www.chem.msu.su/rus/teaching/kovba-pupyshev/kovba-pupyshev-spectra.pdf (стр.12) Здесьψn,k – ядерная волновая функция, ε
n,k – энергетические уровни молекулы, а символы n и k использованыдля указания состояний электронов (n) и состояний ядер (k).
Ядерное уравнение Шредингера описывает поведение двух ядер под действием потенциала En, зависящего лишь от взаимного расположения ядер в пространстве. Из курса физики известно, что подобные "задачи двух тел" можно решить, используя радиус-вектор центра масс и вектор относительного положения ядер: (формула)
В этом случае ядерный гамильтониан оказывается суммой двух гамильтонианов, один из которых – кинетическая энергия центра масс, зависящая лишь от координат центра масс. Этот оператор описывает свободное движение центра масс молекулы (соответствующая волновая функция – это, где k – волновой вектор, показывающий направление импульса центра масс, а энергия поступательного движения центра масс равна (формула). Второй гамильтониан зависит только от переменных
относительного движения R; информация о строении молекулы в основном содержится именно в этом гамильтониане. Поскольку переменные разделяются, функция стационарного состояний будет произведением волновых функций свободного движения центра масс и функции относительного движения частиц, зависящей лишь от R, так что, изучая переходы в молекуле, мы будем рассматривать только изменения этой функции. В классической модели это построение отвечает разбиению энергии молекулы на поступательную и внутреннюю.
После отделения переменных центра масс ядерное уравнение Шредингера (7.1) будет иметь вид: (формула) (7.2),
где R = Ra– Rb, μ – приведенная масса: (формула). В сферических координатах (R,θ,ϕ) оператор Гамильтона в ядерном уравнении запишется как: (формула)(7.3).
Первое слагаемое здесь отвечает кинетической энергии для радиальных (колебательных) движений, а второе имеет вид кинетической энергии вращения. μR2 – это момент инерции ядер относительно центра масс, а LR2 – зависящий лишь от полярных углов оператор квадрата углового момента ядер. Если использовать метод разделения переменных и представить волновую функцию ψ(R) в виде произведения функции χ(R), зависящей только от R, и функции Y(θ,ϕ), зависящей лишь от полярных углов (эти функции известны из квантовой механики как сферические гармоники), то нетрудно выписать уравнение для функции χ(R).
К сожалению, в таком понятном рассуждении есть существенный недостаток. В отсутствиевнешних полей должен сохраняться полныймомент J всей молекулы как целого, а не только угловой момент ядер. Даже если не учитывать дающий очень малый вклад в энергию ядерный спин, то надо было бы полагать, что сохраняется не LR, а J = L + S + LR. Тем не менее, мы заменим оператор квадрата момента в ядерномуравнении на оператор J2(например, ссылаясь на то, что массы ядер намного больше, чем у электронов, а электроны улетают от ядер не слишком далеко. Кроме того, если проделать весьма громоздкие выкладки, приводимое ниже уравнение для радиальной функции тоже получится, но со слегка модифицированным потенциалом). Поскольку момент сохраняется, все состояния молекулы можно классифицировать по собственным значениям оператора квадрата полного момента J2, а они равны. Тогда ядерное уравнение (7.1), будет зависеть только от радиальной координаты (такое ядерное уравнение часто называют радиальным уравнением) и запишется, как: (формула) (7.4).
Энергия молекулы εn,J,v определяется номером электронного состояния n, вращательным квантовым числом J и номером колебательного состояния v. Напомним, что одним и тем же квадратом момента обладают 2J+1 состояний, различающихся проекцией Jz момента на ось z системы координат. Все эти состояния имеют одну и ту же энергию, то есть вырождены. Разумеется, разным значениям Jz соответствуют разные функции YJ,Jz , зависящие от угловых переменных и описывающие вращение молекулы. Радиальная функция отвечает условию нормировки (формула) (множитель R 2возник здесь из-за перехода к сферическим координатам). Поскольку в
таком виде уравнение (7.4) для радиального движения выглядит несколько громоздко, его можно упростить, положив (фомула). Очевидно, условие нормировки для функции u(R) – это обычное условие (формула) =1, а уравнение для неё выглядит как уравнение Шредингера для одной частицы массы μ: (формула) (7.5)
Это уравнение мы будем использовать для описания колебательно-вращательных движений молекулы. Волновую функцию молекулы можно приближенно представить произведением нескольких функций:
а) электронной волновой функции Фn(r,R), получаемой из электронного уравнения Шредингера (4.1),зависящей от радиус-векторов электронов rj
и их спиновых переменных, а также, как от параметров, от радиус-векторов всех ядер R,
б) волновой функции свободного движения центра масс молекулы - e±i(k,Rcm),
в) вращательной части волновой функции YJ,Jz , зависящей лишь от угловых переменных, описывающих поворот молекулы как целого,
г) колебательной волновой функции un,J,v(R), удовлетворяюшей уравнению (7.5).
При сделанных приближениях энергия молекулы – это сумма энергии свободного движения центра масс (поступательной энергии) и электронно-колебательно-вращательной энергии εn,J,v.
Электронно-колебательно-вращательную энергию молекулы можно получить, решая уравнение (7.5). На рисунках 2, 3 приведены результаты численного решения такойзадачи. (Следует отметить, что, решая ур.(7.5) мы определим не только электронно-колебательно-вращательную энергию, но и колебательную волновую функцию un,J,v(R), соответствующую этому энергетическому состоянию молекулы.) Для решения уравнения (7.5) необходимо знать функцию En(R) (электронную энергию или потенциал ядерного уравнения), являющуюся решением электронного уравнения Шредингера (4.1). Она может быть задана просто поточечно, однако очень часто потенциал En(R) аппроксимируют подходящей аналитической функцией. Вблизи точки минимума (R = Re) электронную энергию можно разложить в ряд, первые члены которого в квадратичном приближении будут иметь вид En(R) ≈ En(Re) + kn(R–Re)2/2, где kne – вторая производная потенциала в точке Re: (формула).При J = 0 уравнение (7.5) с таким потенциалом нетрудно решить, так как это просто задача о
гармоническом осцилляторе: (формула) (8.1)
Значения энергии в такой задаче определяется как: (формула); где
(Формула)– классическая частота колебаний тела массы μ на пружине с силовой постоянной ke, v – номер колебательного уровня,En - электронная энергия данного электронного состояни при равновесном межъядерном расстоянии (Re). Волновые функции un,v(R–Re) выражаются как произведение полинома Эрмита и функции вида
exp(–β(R–Re)2) с некоторым коэффициентом β, т.е. быстро спадают при удалении от точки R = Re. Если вернуться к первоначальной задаче с потенциалом En(R), то с помощью сделанной оценки в гармоническом приближении можно методами теории возмущений вычислить значение энергии колебательного уровня с номером v более точно. При этом оказывается, что поправка к энергии оценивается рядом по степеням величины (v+1/2). В итоге получается ряд, обозначения и выбор знаков коэффициентов (колебательных постоянных) которого – спектроскопическая традиция: (формула) (8.2)
Величина ћωexe(v+1/2)2 называется поправкой на ангармоничность, а коэффициент ωexe – коэффициентом ангармоничности. Отметим, чтосогласно уравнению. (8.2) с ростом колебательного квантового числа vрасстояние между соседними уровнями энергии становится все меньше и меньше, тогда как в простом гармоническом приближении расстояние между колебательными уровнями остается величиной постоянной. Для аппроксимации функции En(R) часто используют потенциала Морзе:(формула). Точное решение ур.(7.5) с таким потенциалом соответствует выражению (8.2), если оборвать ряд на квадратичном по (v+1/2) слагаемом: (формула) (8.3)
Тогда можно найти и явные выражения для гармонической частоты ωe и коэффициента ангармоничности ωexe через параметры потенциала α и D: (формулы). В этом случае расстояние между колебательными уровнями энергии линейно зависит от v: εnv+1 – εnv = ћωe – 2ћωexe(v+1/2). По выполнению такого линейного соотношения часто судят о применимости модели Морзе. Отметим, что число колебательных состояний для потенциала Морзе конечно (в отличие от гармонического потенциала) – максимально возможное значение v можно найти из условия εnv+1 – εnv ≥ 0, т.е. v≤ωe/(2ωexe)–1/2.
Поведение радиальных функций un,0,v(R) колебательных движений ядер (при J = 0) можно понять из рисунка 2. Как видно из рисунка, при малых значениях колебательного квантового числа v волновые функции очень похожи на волновые функции гармонического осциллятора. Для R, отвечающих области, в которой двигалась бы классическая частица, т.е. между точками, в которых энергия частицы равна потенциалу (их называют "точками поворота"), функции осциллируют. В классически запрещенных областях (где потенциал больше энергии) функции быстро спадают. Важно отметить, что даже при относительно небольших v колебательные волновые функции заметно отличны от нуля возле точек поворота. Это можно объяснить тем, что (по классическим представлениям) наиболее велика вероятность найти частицу в тех областях, где скорость её мала, то есть именно в окрестностях точек поворота. Описанное явление лучше видно на рисунке 3, изображающем распределение ядерной плотности в тойже системе.
(2 жопных не копирующихся рисунка)
Заметив, что волновые функции гармонического осциллятора локализованы возле равновесного расстояния, мы можем применить теорию возмущений и для учета энергии вращения. Применение теории возмущений даст поправки к энергии в виде ряда по степеням J(J+1). Например, в первом порядке теории возмущений надо просто рассмотреть среднее значение оператора (формула) на функциях unv(R–Re) гармонического осциллятора. Разложив оцениваемый потенциал в ряд по степеням (R–Re), находим, что при некоторых коэффициентах с 2, с3,. поправка к энергии имеет вид:
(формула) где Bv, Dv, Hv … являются рядами по степеням (v+1/2).
Выписанное выражение для энергии позволяет, как и в классической модели
молекулы, представить внутреннюю энергию как сумму электронной (Eеn), колебательной и вращательной энергии: E = Ee + Evib +Erot. Состояние молекулы задается указанием электронного состояния (n; обычно указывается символ электронного состояния, например, 2П), колебательным (v) и вращательным (J) квантовыми числами. В самом грубом приближении (жесткий ротатор) можно пренебречь зависимостью Bv от v и вообще не рассматривать остальные вкладыво вращательную энергию.
17. Понятие "электронная конфигурация". Метод многоконфигурационного самосогласованного поля (МК ССП). Метод конфигурационного взаимодействия (КВ). Одноконфигурационное приближение: метод Хартри-Фока. Понятие "электронная корреляция". Ферми-корреляция и кулоновская корреляция.
Электронная конфигурация — формула расположения электронов по различным электронным оболочкам атома химического элемента или молекулы.
Метод многоконфигурационного взаимодействия (Multi-Configurational Self-Consistent Field – MCSCF) можно рассматривать как метод КВ, в котором оптимизируются не только коэффициенты перед детерминантами, но и коэффициенты разложения МО по АО.
Метод конфигурационного взаимодействия основан на вариационном принципе, аналогично методу Хартри – Фока. Пробная функция записывается в виде линейной комбинации детерминантов, и коэффициенты определяются из условия минимума энергии. Детерминанты классифицируют на однократно (s), дважды (d), трижды (t) и т.д. возбужденные, и функция конфигурационного взаимодействия приобретает следующий вид:
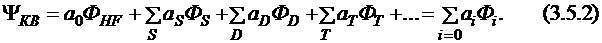
Применяя вариационный принцип, получаем набор секулярных уравнений:
(H - E I) a = 0; (3.5.3)
или:
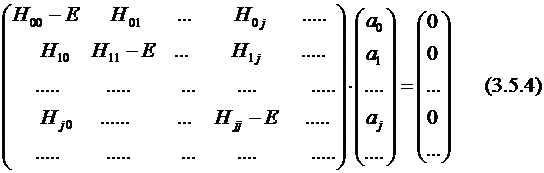
Здесь H – матрица конфигурационного взаимодействия (КВ),
I – единичная матрица.
Матричный элемент матрицы КВ вычисляется из детерминантов: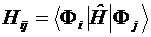 
. Если два детерминанта отличаются друг от друга более чем двумя пространственными молекулярными орбиталями (МО), то всегда будет существовать интеграл перекрывания между двумя разными МО, который равен нулю. Элементы матрицы КВ могут быть, следовательно, отличны от нуля, если два детерминанта одинаковы или отличаются одной или двумя МО, и они могут быть выражены через интегралы одно- и двухэлектронных операторов и МО. Эти соотношения известны