| Женщины в возрасте 15-50> | 38,9 | 30,6 | 30,0 | 31,2 | 32,7 | 34,3 | 34,4 | 37,5 |
| Возрастом от 15 до 19 | 55,1 | 32,1 | 29,3 | 29,2 | 29,0 | 29,6 | 28,6 | 29,5 |
| 20-24 | 119,1 | 94,9 | 90,7 | 91,3 | 92,3 | 93,4 | 88,8 | 92,2 |
| 25-29 | 65,7 | 57,7 | 58,7 | 62,7 | 67,1 | 70,6 | 71,7 | 79,4 |
| 30-34 | 27,5 | 26,5 | 27,6 | 30,2 | 33,0 | 35,4 | 37,7 | 42,7 |
| 35-39 | 9,9 | 8,7 | 9,0 | 9,8 | 10,9 | 12,2 | 13,3 | 15,5 |
| 40-44 | 2,1 | 1,9 | 19,9 | 1,9 | 2,0 | 2,2 | 2,3 | 2,5 |
| 45-49 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |
| Количество детей, которое может родить в среднем одна женщина | 1,4 | 1,1 | 1,1 | 1,1 | 1,2 | 1,2 | 1,2 | 1,3 |
Коэффициенты рождаемости, приведённые в таблице 1.2, свидетельствуют, что в Украине наиболее детородными являются женщины в возрасте 20-24 года. Об этом убедительно свидетельствует динамика коэффициентов рождаемости. После 24 лет, то есть с возрастом количество рождающихся детей стабильно уменьшается.
Дисперсионный анализ
Статистическое исследование вариации варианта ряда распределения связано, прежде всего, с практической необходимостью. В каждом конкретном случае их роль и значение определяются информацией на выходе, а также социально-экономическим значением исследуемого показателя. Что касается первого, то тут невозможно дать однозначный ответ. В частности, как быть в случае, когда в исследуемой совокупности значения отдельных вариантов существенно отличаются от всей совокупности и не являются типичными. Возьмём для примера ряд распределения, который характеризует годовой уровень доходов в пересчёте на одно домохозяйство. В таком ряду могут находиться домохозяйства с размером годового дохода, который не превышает 10000 грн., и такие размер доходов которых превышает миллион и более денежных единиц.
В экономической литературе по этому поводу не существует единой точки зрения. Одни учёные предлагают исключать нетиповые уровни исследуемого признака, другие эти действия считают незаконными по отношению к фактическим данным.
Наиболее приемлемым подходом является тот, при котором в каждом конкретном случае необходимо руководствоваться социально-экономическим значением исследуемого явления. Действительно, в случае, когда размер заработной платы работников бригады в месяц составил соответственно: 1200, 1700, 2200, 2700, 10000 условных единиц, то для статистической оценки объёмов месячного фонда заработной платы в целом нельзя исключать работника, который получил заработную плату 10000 условных единиц. Вместе с тем при подсчёте типовой для бригады средней заработной платы в месяц, заработную плату размером 10000 условных единиц необходимо исключить из исследуемого ряда распределения.
Вариация признака, в каждом конкретном случае, характеризуется позитивно или негативно, является желательной или нежелательной. Для практической и познавательной деятельности важным является познание роли и значения тех или иных факторов в формировании вариации признака. С этой целью используют дисперсионный анализ. В основе такого анализа лежит закон разложения общей дисперсии 
на систематическую 
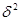(дельта) и случайную 
, или:
,
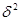где - общая дисперсия; - межгрупповая дисперсия (систематическая, факторная); - случайная дисперсия.
Общая вариация варьирует под влиянием систематических и случайных факторов.
Систематическая вариация или факторная является результатом действий постоянных, систематических факторов.
Случайная вариация – часть общей вариации, вызванная действием случайных факторов.
Дисперсионный метод анализа тесно связан с аналитическим группированием и построен с учётом теоретических и методологических условий проведения аналитического группирования. Прежде всего на основании логического экономического анализа определяют факторные и результативные признаки. Сравнивая групповые средние результативного признака с факторным, устанавливают наличие и размер связей, взаимозависимостей между причинами и следствиями.
Совместное использование дисперсионного и группировочного методов измерения взаимосвязей подразумевает расчёт межгрупповой (факторной) и внутригрупповой (случайной) дисперсии наряду с расчётом общей дисперсии. Межгрупповая вариация носит название систематической и характеризует влияние на результирующий признак систематических факторов, а её размер определяют с помощью формулы межгрупповой дисперсии:
,
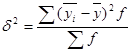где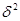 
- межгрупповая дисперсия; 
- среднее значение групп; 
- общая средняя; 
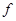- частота.
Учтём, что межгрупповая дисперсия характеризует отличия, вариацию групповых средних около общей средней .
Случайная вариация, которая вызвана действием всех остальных факторов, за исключением фактора, который положен в основу группирования, оценивается с помощью внутригрупповой дисперсии. Она является средней величиной групповых дисперсий и расчитывается по формуле:
.
Внутригрупповая дисперсия рассчитывается отдельно для каждой группы:
,
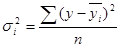где 
- значение признака отдельных элементов совокупности.
Для установления тесной связи между признаками межгрупповую дисперсию сравнивают с общей. Отношение межгрупповой дисперсии к общей называется корреляционным. Его обозначают греческой буквой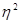 
(эта) и рассчитывают по формуле:
.
Корреляционное отношение может изменяться от 0 до +/-1. В случае если 
=0 – межгрупповая дисперсия равняется нулю, а связь между факторным и результирующим признаками отсутствует.
Если 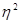=1, то межгрупповая дисперсия равна общей, а внутригрупповая равняется нулю. Связь функциональная. Чем ближе значение 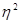к 1, тем теснее связь.
Рассмотрим пример расчёта дисперсий, используя данные из таблицы 3.
Таблица 3