Теор-практикум. Поток. Ч.1.
Задание №1
Повторим математику.
1. Найти корни уравнения 
.
2.Вычислить 
3.Записать ряды Маклорена для функций, используя известные разложения: 
.
4.Исследовать функцию
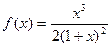
и построить эскиз графика.
5. Найти все значения корня (формула Муавра)
и изобразить их на комплексной плоскости.
6. Найти общее решение
y(4) + y′ =0.
7. Записать общее решение дифференциального уравнения
y″ + 9y = 0 в трёх разных видах (формах).
Векторы и произведения векторов.
8. Даны векторы в координатной форме
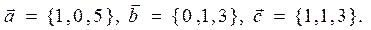
8a) Вычислить 
8б) Найти высоту пирамиды построенной на векторах 
опущенную на плоскость векторов 
9. Распознать и изобразить кривые второго порядка: 
.
10. Сложная функция имеет вид F(x,y) = x 2 + ysin x; где x = e2 t+s , y = tg(t+s).
Вычислить 
.
Задание №2
Преобразования Галилея и Лоренца.
Теория. Что такое абберация света? Что измерялось в опытах Физо и Майкельсона? Каковы результаты этих опытов? Почему результат опыта Майкельсона называют отрицательным?
1. Две частицы с массой m1 и m2 связаны абсолютно упругой пружиной (
). Записать уравнения Ньютона для этих частиц в системе К и К′ (см. лекцию).
2. Вычислить функцию для преобразований координат из системы К в инерциальную систему и К′ (см. лекцию), оставляющих неизменными фронт световой волны.
Указание: приравнять [ ]2x’t’=0.
3. Закон сложения скоростей в СТО. Скорости частиц во встречных пучках равны: а) v1 = 1/3c = - v2; b) v1 = 2/3c = - v2; 3) v1 =0,99c = - v2, где с-скорость света. Определить скорость одной частицы в системе отсчета, в которой другая покоится. Нарисовать эскизы относительного движения систем отсчета и частиц в них; сделать выводы.
4. Записать ряды Маклорена для 
и 
в галилевской интерпретации
опыта Майкельсона.
5. В системе К частица движется по закону x = 0; y = 0; z = - ct. Найти с помощью преобразования Галилея и Лоренца ее скорость в системе К′, движущейся со скоростью V (см. лекции). Выводы.
6. Звезда расположена под углом α к горизонту, то есть 
. Найти проекции скорости света для наблюдателя, движущегося со скоростью V, и угол, под которым он увидит звезду. Что можно сказать о количестве и цвете звезд, наблюдаемых в носовой и кормовой иллюминаторы?
7. Расстояние до звезды α-Центавра равно 4,3 световых года. Космический корабль полетит со скоростью v = 0,95 c, где c − скорость света. На сколько суток надо запасать продукты, если: а) космонавты не учили СТО; b) они ее учили.
8. Вывести формулу для ускорения тела, равномерно движущегося по окружности.
9. Из пункта А в пункт В вниз по реке пароход плывет сутки, а обратно двое. За какое время можно сплавится из А в В на плоту?
Задание №3
1. Решить задачу о движении заряженной частицы в постоянном электрическом поле 
с нулевыми начальными условиями v (0) = r (0) = 0 с помощью уравнения Ньютона. Эту же задачу решить с помощью уравнения Эйнштейна – Ньютона. Сравнить полученные результаты. (Построить графики v(t) и r(t) = x(t). Результат объяснить. Определить типы кривых x=f(t)), в каждом из рассмотренных случаев.
2. Вывести связь между работой силы и кинетической энергией релятивистской частицы (доказать правильность формул (9.4), (9.6), (9.7) по лекциям. Провести сравнения с подобными результатами механики Ньютона.
3. Вычислить энергию необходимую для того, чтобы частице массой 1г сообщить скорость 0,9с, с – скорость света. Вычислить энергию необходимую для увеличения скорости у этой частицы от 0,9с до 0,95с; тоже -- от 0,95с до 0,99с. Результат объяснить.
4. Найти длину n-ой трубки дрейфа ЛРУ, если частота ускоряющего поля w, а энергия приобретаемая в зазоре e×ΔU.
5. Проверить на a-радиоактивность изотоп 239Pu и вычислить импульсы и кинетические энергии продуктов распада Проверить на радиоактивность 39Ar и вычислить максимальную энергию электрона.
6. Какая энергия выделяется при сгорании 1г смеси деитерия-трития в термоядерной реакции 
?
7. Построить из кварков первого поколения барионы: протон, нейтрон и мезоны: π+, π- и π0.
Задание №4
1. Записать матрицы поворота вокруг координатных осей на плоские углы альфа, вокруг Z; бетта, вокруг Y; гамма, вокруг X с помощью матрицы поворота в пространстве.
2. Записать матрицу поворота на пространственный угол, определяемый последовательными поворотами на плоские углы, из задачи 1 и найти координаты единичного вектора к ={0,0,1} в новом базисе.
3. Доказать, что det L =1, L∙LT = E, где L - матрица Лоренца.
4. На какую энергию должен работать электрон - позитронный коллайдер чтобы получить инвариантную энергию в системе инерции сталкивающихся частиц такую же, как при столкновении ускоренного в станфордском ускорителе до 50 ГэВ позитрона при столкновении с покоящимся электроном?
5. Будет ли идти реакция 
при энергии Еg = 155МэВ в лабораторной системе?
Найти инвариантную энергию этой реакции (МэВ) при
Еg=320МэВ в лабораторной системе.
Какой импульс больше по величине, фотона или протона в
СЦИ? Чему равны эти импульсы при Еg=320МэВ.
6. Найти максимальный импульс электрона при распаде нейтрона.