Теор-практикум. Поток.Ч.2.
Физические постоянные
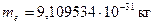
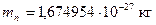
Занятие № 1(5)
1. Определить размерности величин 
, 
, где p - импульс, l - длина, E - энергия, t - время.
2. Чему равен 1 г вещества в единицах МэВ/c2 ? Чему равен импульс тела 1г *м/сек в единицах МэВ/c?
3. Найти длины волн, соответствующие красной границе фотоэффекта и скорости фотоэлектронов, выбиваемых из Zn, Ag, Ni (работа выхода равна 3,74, 4,28 и 4,84 эВ) светом с длиной волны 0,27 мкм.
4. Найти длину волны де Бройля для электронов и протонов с кинетической энергией 1 кэВ, для пули (m =10 г, v =100 м/с), для человека, бегущего стометровку (m =70 кг), для теплового нейтрона (T =0,025 эВ). Можно ли экспериментально наблюдать дифракцию этих объектов?
Занятие 2(6)
1. Доказать, что произведение двух линейных операторов 
и 
является линейным оператором.
2. Определение: оператор называется самосопряженным, если 
Какие из операторов являются самосопряженными, если непрерывные функции 
и 
заданы на отрезке [ a,b ], причём 
, 
.
а) 
б) 
в) 
г) 
Следствие: операторы (
) и 
- самосопряженные.
3. Вычислить коммутаторы
а) 
б) 
в) 
г) 
4. Пусть 
, вычислить коммутаторы
а) 
б) 
в) 
г)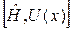 
.
5. Показать, что если оператор в уравнении
эрмитов, то его собственные значения - вещественны.
6. Доказать, что если операторы и эрмитовы и коммутируют, то оператор 
- эрмитов.
Занятие № 3 (7)
1. Задача на собственные значения и функции
а) Найти собственные функции оператора в уравнении
отвечающие вещественным собственным значениям 
.
б) Найти функции удовлетворяющие следующим граничным условиям на отрезке: 
, 
.
в) Проверить ортогональность собственных функций и нормировать их.
|
|
г) Как характеризовать спектр собственных значений оператора? Найти спектр.
2. У оператора дискретный спектр собственных значений и вещественные собственные функции,
,
среди которых есть две вырожденные. Ортогонализовать вырожденные функции на области определения функций 
. Попробуйте это сделать в случае трех вырожденных функций.
3. При каких собственных значениях оператора 
его собственные функции будут периодическими? Чему равен период?
- Самостоятельная работа по лекции.
Частица в 1-D потенциальной яме с бесконечно высокими стенками
1. Записать и решить уравнение Шредингера для частицы массы m, которая находится в потенциальном поле следующего вида:
2. Доказать ортогональность собственных функций.
3. Нормировать собственные функции.
4. Нарисовать эскизы квадрата модуля волновой функции для четных и нечетных n (n =1..5).
5. Вычислить средние значения координаты и импульса частицы в состоянии 
.
Занятие № 4 (8) - Туннельный эффект
1. На лекции было получено:
.
а) Доказать для E > U 0, что коэффициент прозрачности D, 
,
равен
.
б) Показать, что при 
:
,
где 
.
в) Получить упрощенную формулу для коэффициента прозрачности:
,
если 
, а a α >> 1.
2. Оценить коэффициент прозрачности для электрона и протона, если D0 = 1, U0 – E =10-18 Дж, a =10-10 м. Чему равен коэффициент отражения?
3. Оценить для альфа-частицы коэффициент прозрачности барьера, если его ширина равна 2,5∙10-15 м, а U0 – E = 7 МэВ. Принять D0 = 1.Каков период полураспада соответствующего альфа-радиоактивного ядра?
|
|