Расчет упругих железобетонных труб

 

Расчет геометрических параметров. Требуемую площадь спиральной арматуры на 1 пог. м стенки трубы вычисляют по формуле:

 

 

где а — безразмерный коэффициент, равный 4-5; R_р — расчетное сопротивление спиральной арматуры растяжению.

Назначают диаметр спиральной арматуры d_p и вычисляют соответствующую площадь поперечного сечения А_р1.

Определяют число витков на 1 пог. м расчетного продольного сечения стенки трубы и округляют до целого числа:

 

Уточняют общую площадь спиральной арматуры:

 

Вычисляют шаг витков: t = b/n_p.

Необходимо соблюдать следующие условия:

 

 

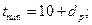
где h — толщина стенки трубы, мм; d_p — диаметр арматурной проволоки, мм; а₀ — толщина защитного слоя бетона, мм.

Последовательно определяют необходимые в дальнейшем геометрические параметры расчетного сечения (рис. 33).

 

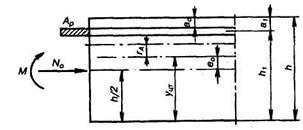Рис. 33. Геометрические параметры сечения стенки трубы

Площадь приведенного сечения:   Ared = A в +nAp,   где А в — площадь бетона расчетного сечения; n — отношение модуля упругости арматуры к модулю упругости бетона

 

56

Статический момент приведенного сечения относительно внутренней грани:

 

Здесь a₁ — расстояние от наружной грани до центра тяжести спиральной арматуры; b — ширина расчетного сечения.

Расстояние от внутренней грани до центра тяжести приведенного сечения:

Момент инерции продольного приведенного сечения относительно оси, проходящей через центр тяжести,

 

 

Момент сопротивления продольного приведенного сечения стенки трубы для внутренней грани:

 

где Ψ_Т — коэффициент, учитывающий развитие пластических деформаций бетона.

Расстояние между точками приложения силы обжатия и центром тяжести приведенного сечения (эксцентриситет):

 

Положение условной ядровой точки, наиболее удаленной от сечения, проверяемого по образованию трещин, определяется расстоянием:

 

 

где W_red — момент сопротивления сечения без учета развития пластических деформаций.

Потери предварительного напряжения от релаксации спиральной арматуры:

 

57

где σ_р — предварительное напряжение в арматуре без учета потерь, соответствующих нулевым напряжениям в бетоне:

σ_р = 0,75 R_p,_Ser; здесь R_р,Ser — расчетное сопротивление растяжению спиральной арматуры класса BII.

Если вычисленное значение σ₁ окажется отрицательным, его следует принять равным нулю.

Потери предварительного напряжения в арматуре, вызванные деформацией бетона от быстронатекающей ползучести:

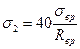при

при

 

где R _{в p} — прочность бетона в момент передачи усилия обжатия, которую принимают равной 0,9 прочности бетона заданного проектного класса; σ _{в р} — напряжения в бетоне на уровне центра тяжести спиральной арматуры:

 

 

Здесь N₀₁ — начальное усилие, передающееся на бетон от спиральной арматуры с учетом потерь от релаксации напряжений в арматуре:

 

у — расстояние от центра тяжести приведенного сечения до центра тяжести спиральной арматуры:

 

 

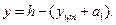
Потери предварительного напряжения в спиральной арматуре, вызванные деформациями ползучести бетона:

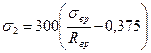при

при

Здесь σ _{в р} — то же, что в предыдущем случае, но с учетом потерь σ₁ и σ₂.

 

58

Потери напряжения в спиральной арматуре от усадки вибро-гидропрессованного бетона σ₄ составляют 15 МПа для бетона класса В3О, 20 МПа для В40 и 25 МПа для бетона класса В50.

Суммарные потери напряжения в арматуре расчетного сечения трубы:

 

 

Опрессовочное давление вычисляют по формуле:

 

 

где N_o1 — усилие обжатия; р_п — потери опрессовочного давления: р_п = 0,3 МПа; b — ширина расчетного продольного сечения стенки трубы; r _а — радиус окружности, по которой располагается центр тяжести спиральной арматуры: r _a = 0,5 d-a₁.

Расчет неотрываемости бетона защитного слоя. Радиальное напряжение определяют по формуле:

 

 

где А — коэффициент, вычисляемый по формуле:

 

 

Здесь

;

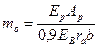где Е_р и Е_b — модули упругости соответственно напрягаемой арматуры и бетона.

Неотрывность защитного слоя бетона будет обеспечена, если соблюдается условие:

где R_Bt, _Sez — расчетное сопротивление бетона осевому растяжению; К — коэффициент концентрации напряжений в бетоне, К =3.

 

59

Расчет прочности продольного сечения стенки трубы выполняется по первой группе предельных состояний на воздействие расчетного изгибающего момента от давления грунта засыпки и транспортной нагрузки НК-80. Прочность будет обеспечена, если соблюдается следующее условие:

где R_вt — расчетное сопротивление бетона осевому растяжению;

N_o — сила обжатия бетона после проявления всех потерь:

 

 

М — расчетный изгибающий момент.

Проверку трещиностойкости виброгидропрессованных труб выполняют по условию:

 

где R_{вt, sez} — расчетное сопротивление бетона осевому растяжению при расчетах по второй группе предельных состояний; W^T_red - приведенный момент сопротивления расчетного сечения с учетом развития пластических деформаций; М _n — нормативный изгибающий момент; М^я_об — момент силы обжатия относительно ядровой точки:

 

 

Заметим, что по данным исследований НИИЖБ прочность виброгидропрессованного бетона примерно в 1,4 — 1,8 раза выше, чем вибрированного. Это дает основание принимать при расчетах повышенные значения характеристик по сравнению с рекомендуемыми СНиП. В первом приближении рекомендуются следующие коэффициенты перехода от прочности вибрированного бетона к прочности виброгидропрессованного: по сжатию — 1,3, по растяжению — 1,15.