Методичекие указания
Большинство алгоритмов для получения псевдослучайных чисел имеют вид xi+ 1= F (xi), где F – совокупность операций, которые надо проделать над числом xi, чтобы получить xi+ 1.
Так, широко известные способы имитации равномерно распределенных случайных чисел основаны на реализации рекуррентного соотношения
xi +1= j(xi,…, xi-r)(mod m) (1)
и определяют xi +1 как наименьший неотрицательный вычет j(xi,…, xi-r) по модулю m (т.е. остаток от деления на m).
В зависимости от того, является ли функция j линейной или нет, различают линейные и нелинейные методы.
Метод мультипликативного сравнения или метод вычетов. При данном методе задаются двумя определенным образом подобранными целыми числами: множителем a и модулем m. Последовательность случайных чисел вычисляется по следующему алгоритму:
| Шаг 1. | Число xi известно с предыдущего шага. Вычисляется произведение axi. |
| Шаг 2. | Число axi делится на m. Получается целое число q и целочисленный остаток xi +1, что можно представить в виде axi = qm + xi +1, 0 £ xi +1 £ m –1. |
| Шаг 3. | Так как xi +1 – число между 0 и m, то нужно его еще разделить на m, чтобы получить число между 0 и 1: yi+1= xi +1/ m. |
Таким образом, соотношение (3.1) записывается в виде
xi +1= axi (mod m). (2)
При этом говорят, что числа axi и xi +1 сравнимы по модулю m, т.е. они являются равноостаточными при делении на m. Формулу (3.2) называют сравнением по модулю, а остаток xi +1 – наименьшим положительным вычетом по модулю m. Этим объясняются оба названия алгоритма – метод мультипликативного сравнения или метод вычетов.
Алгоритмы наиболее часто применяемых в настоящее время генераторов равномерно распределенных случайных величин в общем виде можно описать следующим образом:
 , (3)
, (3)
где коэффициенты a 0, a 1, …, ar, m и m, а также получаемые числа x 1, x 2, … – целые числа.
Линейные (конгруэнтные) генераторы образования равномерно распределенных чисел на интервале [0; 1) можно представить так:
yi +1 = xi +1 m -1. (4)
Мультипликативный генератор. Рассмотренный выше пример получения случайных последовательностей методом мультипликативного сравнения является частным случаем линейного генератора. Подставляя в (3.3) m = a 1= … = ar =0 и положив, что a 0 > 0, получим:
xi +1= a 0 xi (mod m). (5)
На практике генератор вида (3.5) обладает достаточно хорошими статистическими характеристиками.
Смешанный генератор получится, если в (3) положить a0 > 0, m > 0, а a 1= a 2 =… = ar = 0:
xi +1= (a 0 xi +m)(mod m). (6)
Аддитивный или генератор Фибоначчи. Если в (3.) задать m = a 2=…= = ar = 0 и a0 = a1 = 1, то генератор такого вида описывается выражением:
xi +1= (xi + xi- 1)(mod m). (7)
Обобщенным аддитивным генератором или обобщенным генератором Фибоначчи называетсягенератор вида (3), где все ai = 1.
Пример. Рассмотрим смешанный генератор:
(1255·135+10555) (mod 1000) = 179980 (mod 1000) = 980
(1255·980+10555) (mod 1000) = 1240455 (mod 1000) = 455
Таким образом, по целым числам последовательности { xi } можно построить последовательность{ xi /m} рациональных чисел из единичного интервала. Например, 0,98; 0,455 и т.д.
Задача 2
Воспользовавшись таблицей равномерно распределенных чисел, приведенных в Приложении сформировать последовательность 30 чисел Ba ; b; p имеющих распределение Бернулли и проверить основные статистические характеристики полученных последовательностей
Таблица 2.1
| m | ||||||||||
| a | 0,5 | 1,5 | ||||||||
| b |
Таблица 2.2
| m | ||||||||||
| p | 0,1 | 0,15 | 0,2 | 0,25 | 0,3 | 0,35 | 0,4 | 0,45 | 0, 5 | 0,6 |
Методические указания
Случайная величина X имеет распределение Бернулли с параметрами a, b, p, где a < b и 0 < p < 1, если она принимает только значения a и b, причем P (X = a) = 1 – p, P (X = b) = p.
Обозначим такую случайную величину Ba ; b; p . Стандартную величину Бернулли с параметрами a = 0, b = 1 будем обозначать Bp.
В качестве примера на рис. 1 приведены графики плотности распределения вероятностей w (x) и функции распределения F (x) для B 0;2;0,7.

Рис. 1. Графики ПРВ и ФР для распределения Бернулли:
a – ПРВ; б – ФР
Ниже приведены формулы для вычисления статистических характеристик распределения Бернулли B a ; b; p :
| плотность распределения веросятностей – | 
|
| функция распределения – | 
|
| математическое ожидание – | 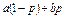 , ,
|
| дисперсия – |  , ,
|
Для моделирования случайной величины Ba ; b; p нужно:
1) получить значение случайной величины U с равномерным распределением на отрезке [0, 1);
2) если U < p, то положить Ba ; b; p = b, в противном случае положить Ba ; b; p = a.
Задача 3
Воспользовавшись таблицей равномерно распределенных чисел, приведенных в Приложении 1 сформировать последовательность 20 чисел Ba ; b; p имеющих биномиальное распределение и проверить основные статистические характеристики полученных последовательностей
Таблица 3.1
| m | ||||||||||
| n |
Таблица 3.2
| m | ||||||||||
| p | 0,1 | 0,15 | 0,2 | 0,25 | 0,3 | 0,35 | 0,4 | 0,45 | 0, 5 | 0,6 |
Методические указания
Случайная величина X имеет биномиальное распределение с параметрами n, p, где n = 1, 2,... и 0 < p < 1, если она имеет вид
 (8)
(8)
где Bp (i) (i =1, 2,..., n) – независимые стандартные бернуллиевские величины с одним и тем же параметром p.
В качестве примера на рис. 2 приведены графики ПРВ и ФР для распределения B 10; 0.3.

Рис. 2. Графики ПРВ и ФР для биномиального распределения:
а – ПРВ; б – ФР.
Ниже приведены статистические характеристики биномиального распределения B n;p:
| плотность распределения вероятностей – |  , ,
|
| функция распределения – |  , ,
|
| математическое ожидание – |  , ,
|
| дисперсия – |  . .
|
Моделирование значений случайной величины B n ; p производится с использованием определения (8), в котором стандартные бернуллиевские величины формируются аналогично способу, изложенному выше.
Получение значений случайной величины Х с биномиальным распределением вероятностей заключается в следующем:
1) реализуется случайная величина R, равномерно распределенная на интервале [0;1);
2) для каждого члена последовательности { rn } проверяется выполнение неравенства ri < p (i = 1, 2, …, n). Если неравенство выполняется, принимается Xi = 1, в противном случае Xi = 0;
3) вычисляется сумма значений n случайных величин Xi, которая и принимается за значение случайной величины X = s.
При повторении этой процедуры k раз получаем последовательность значений s 1, s 2, …, sk, которые являются реализацией биномиально распределенной случайной величины X.
Пример. Получить случайные числа, отвечающие биномиальному распределению с параметрами n = 10, p = 0,35. Для этой цели воспользуемся таблицей равномерно распределенных случайных чисел. Пусть { rn }: 0,367; 0,417; 0,967; 0,895; 0,214; 0,882; 0,266; 0,234; 0,191; 0,795.
Четыре из этих чисел не превосходят p = 0,35. Следовательно, случайная величина приняла значение X = s = 4.
Если требуется сформировать последовательность из 50 чисел, данную операцию следует повторить 50 раз.
При проверке соответствия выработанной последовательности чисел биномиальному распределению используют выражение начальных моментов 1-го и 2-го порядков. Если для заданных n и p в последовательности, полученной в результате моделирования, содержится M чисел si, то должны приблизительно выполняться равенства
 . (9)
. (9)
ПРИЛОЖЕНИЕ
Выборка независимых одинаково распределенных чисел с распределением R (0,1).
0.795 0.235 0.203 0.891 0.641 0.741 0.492 0.266 0.203 0.011
0.394 0.751 0.530 0.574 0.200 0.527 0.604 0.370 0.565 0.636
0.396 0.747 0.698 0.433 0.618 0.688 0.150 0.352 0.304 0.956
0.009 0.408 0.642 0.868 0.601 0.266 0.514 0.164 0.349 0.543
0.347 0.125 0.101 0.086 0.381 0.853 0.149 0.478 0.863 0.646
0.009 0.174 0.267 0.046 0.870 0.831 0.262 0.981 0.492 0.430
0.432 0.772 0.847 0.736 0.735 0.908 0.297 0.483 0.047 0.905
0.537 0.259 0.387 0.744 0.761 0.329 0.447 0.165 0.566 0.752
0.737 0.549 0.057 0.797 0.865 0.508 0.246 0.925 0.889 0.631
0.923 0.886 0.779 0.941 0.054 0.631 0.404 0.017 0.784 0.442
0.015 0.010 0.733 0.031 0.461 0.059 0.345 0.211 0.917 0.325
0.109 0.035 0.377 0.996 0.431 0.877 0.331 0.254 0.003 0.455
0.204 0.720 0.454 0.391 0.257 0.990 0.528 0.984 0.899 0.540
0.291 0.547 0.475 0.122 0.165 0.445 0.736 0.048 0.292 0.790
0.981 0.743 0.257 0.149 0.580 0.313 0.317 0.123 0.641 0.281
0.694 0.299 0.729 0.845 0.672 0.841 0.891 0.489 0.610 0.826
0.560 0.612 0.514 0.808 0.218 0.868 0.714 0.504 0.470 0.201
0.226 0.627 0.393 0.533 0.594 0.611 0.338 0.165 0.643 0.572
0.225 0.458 0.254 0.861 0.013 0.837 0.071 0.292 0.162 0.266
0.126 0.435 0.482 0.877 0.336 0.289 0.143 0.914 0.811 0.179
0.120 0.690 0.514 0.445 0.466 0.130 0.359 0.628 0.293 0.900
0.800 0.592 0.625 0.081 0.887 0.681 0.420 0.039 0.164 0.301
0.662 0.193 0.174 0.227 0.404 0.939 0.932 0.111 0.159 0.634
0.268 0.860 0.789 0.029 0.537 0.191 0.242 0.118 0.062 0.657
0.004 0.933 0.196 0.053 0.392 0.045 0.732 0.718 0.512 0.137
0.652 0.313 0.436 0.291 0.232 0.144 0.431 0.192 0.669 0.722
0.457 0.441 0.996 0.626 0.498 0.969 0.145 0.972 0.600 0.233
0.596 0.292 0.676 0.912 0.705 0.986 0.635 0.117 0.477 0.728
0.050 0.668 0.975 0.268 0.645 0.732 0.880 0.709 0.146 0.094
0.095 0.905 0.512 0.009 0.457 0.804 0.916 0.494 0.093 0.396
0.426 0.807 0.229 0.096 0.715 0.998 0.110 0.200 0.193 0.491
0.464 0.056 0.887 0.064 0.315 0.442 0.453 0.285 0.524 0.973
0.497 0.785 0.611 0.773 0.357 0.501 0.323 0.862 0.187 0.654
0.988 0.682 0.443 0.322 0.332 0.327 0.892 0.587 0.487 0.559
0.020 0.958 0.309 0.290 0.349 0.440 0.316 0.271 0.309 0.423
0.225 0.954 0.356 0.916 0.697 0.216 0.311 0.336 0.260 0.958
0.544 0.905 0.515 0.377 0.102 0.687 0.828 0.934 0.454 0.139
0.657 0.256 0.797 0.183 0.283 0.714 0.685 0.698 0.367 0.138
0.500 0.938 0.594 0.255 0.793 0.929 0.401 0.732 0.975 0.977
0.867 0.775 0.420 0.320 0.208 0.529 0.692 0.133 0.293 0.559
0.739 0.077 0.347 0.094 0.044 0.259 0.760 0.579 0.236 0.255
0.316 0.312 0.039 0.774 0.619 0.557 0.245 0.500 0.239 0.875
0.231 0.592 0.016 0.580 0.170 0.657 0.788 0.349 0.508 0.039
0.128 0.539 0.562 0.607 0.303 0.377 0.563 0.149 0.215 0.276
0.093 0.761 0.479 0.390 0.779 0.747 0.117 0.404 0.348 0.093
0.189 0.528 0.802 0.668 0.510 0.166 0.517 0.736 0.162 0.825
0.405 0.936 0.840 0.176 0.380 0.621 0.014 0.568 0.886 0.142
0.673 0.442 0.439 0.377 0.910 0.750 0.303 0.825 0.282 0.031
0.384 0.408 0.693 0.906 0.860 0.120 0.425 0.015 0.934 0.061
0.256 0.999 0.523 0.950 0.035 0.917 0.297 0.628 0.154 0.081
0.935 0.225 0.093 0.856 0.932 0.056 0.407 0.101 0.027 0.848
0.410 0.198 0.553 0.658 0.936 0.726 0.694 0.734 0.770 0.028
0.987 0.201 0.014 0.246 0.282 0.637 0.422 0.727 0.338 0.097
0.136 0.041 0.809 0.262 0.979 0.817 0.324 0.429 0.228 0.757
0.931 0.531 0.624 0.973 0.981 0.289 0.563 0.864 0.596 0.173
0.827 0.522 0.164 0.513 0.736 0.269 0.665 0.424 0.815 0.436
0.002 0.453 0.396 0.525 0.997 0.714 0.942 0.486 0.114 0.750
0.820 0.090 0.445 0.016 0.426 0.777 0.160 0.538 0.239 0.977
0.420 0.973 0.531 0.334 0.873 0.759 0.569 0.829 0.381 0.060
0.403 0.674 0.328 0.188 0.998 0.213 0.441 0.189 0.970 0.550
0.896 0.951 0.926 0.971 0.392 0.764 0.419 0.341 0.333 0.152
0.818 0.774 0.749 0.541 0.922 0.444 0.721 0.045 0.295 0.291
0.534 0.549 0.927 0.380 0.381 0.584 0.581 0.674 0.194 0.450
0.598 0.834 0.461 0.478 0.752 0.709 0.045 0.387 0.757 0.195
0.835 0.115 0.614 0.296 0.557 0.991 0.865 0.076 0.684 0.710
0.267 0.802 0.676 0.387 0.783 0.568 0.873 0.603 0.969 0.698
0.320 0.131 0.296 0.855 0.522 0.289 0.412 0.837 0.794 0.924
0.248 0.732 0.924 0.646 0.961 0.467 0.994 0.756 0.326 0.041
0.658 0.606 0.471 0.837 0.924 0.051 0.639 0.116 0.606 0.996
0.451 0.961 0.887 0.463 0.084 0.377 0.160 0.131 0.594 0.775
0.754 0.735 0.080 0.868 0.778 0.304 0.380 0.162 0.599 0.141
0.377 0.503 0.463 0.822 0.188 0.203 0.674 0.889 0.373 0.149
0.858 0.025 0.333 0.918 0.074 0.104 0.081 0.303 0.207 0.984
0.620 0.718 0.882 0.882 0.436 0.381 0.050 0.333 0.410 0.691
0.643 0.604 0.464 0.934 0.113 0.231 0.886 0.762 0.160 0.848
0.134 0.928 0.105 0.191 0.833 0.352 0.518 0.863 0.511 0.784
0.033 0.065 0.381 0.194 0.859 0.473 0.433 0.573 0.931 0.486
0.053 0.589 0.677 0.029 0.864 0.331 0.719 0.670 0.774 0.706
0.624 0.025 0.174 0.688 0.637 0.333 0.461 0.934 0.243 0.592
0.700 0.107 0.039 0.658 0.679 0.783 0.209 0.317 0.565 0.162
0.919 0.308 0.775 0.277 0.092 0.343 0.952 0.105 0.862 0.038
0.525 0.560 0.313 0.113 0.678 0.631 0.220 0.420 0.916 0.557
0.173 0.400 0.352 0.085 0.991 0.726 0.781 0.953 0.734 0.821
0.323 0.004 0.049 0.853 0.229 0.505 0.006 0.453 0.207 0.362
0.494 0.746 0.552 0.902 0.310 0.788 0.549 0.651 0.818 0.040
0.360 0.722 0.175 0.165 0.721 0.115 0.301 0.298 0.247 0.671
0.521 0.821 0.407 0.479 0.105 0.411 0.919 0.250 0.653 0.312
0.489 0.898 0.041 0.889 0.010 0.365 0.983 0.766 0.177 0.060
0.485 0.186 0.251 0.263 0.572 0.465 0.994 0.672 0.580 0.916
0.827 0.511 0.942 0.470 0.790 0.660 0.242 0.508 0.424 0.200
0.995 0.573 0.205 0.759 0.299 0.903 0.240 0.466 0.430 0.915
0.223 0.862 0.753 0.747 0.231 0.343 0.966 0.478 0.351 0.538
0.082 0.081 0.730 0.104 0.927 0.350 0.098 0.760 0.814 0.736
0.898 0.718 0.277 0.491 0.140 0.850 0.982 0.182 0.601 0.948
0.135 0.255 0.451 0.031 0.243 0.463 0.856 0.181 0.521 0.807
0.908 0.298 0.262 0.357 0.189 0.133 0.411 0.917 0.785 0.236
0.542 0.644 0.958 0.324 0.582 0.189 0.737 0.324 0.728 0.355
0.640 0.435 0.318 0.676 0.006 0.232 0.052 0.692 0.251 0.773
0.963 0.376 0.604 0.950 0.941 0.269 0.064 0.614 0.893 0.498
0.132 0.686 0.620 0.847 0.407 0.874 0.999 0.944 0.157 0.026