Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ Государственное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ »
ИНСТИТУТ КИБЕРНЕТИКИ
Расчетно-графическая работа №1:
«Расчет линейной электрической цепи с постоянными напряжениями и токами»
ВАРИАНТ №26
Выполнил: Студент группы 8Т10
Окунев Алексей Вячеславович
Подпись:____________________
Принял: Доцент кафедры ТОЭ
Купцов Анатолий Михайлович
Подпись:_____________________
Томск 2012
Задание
По номеру варианта составить граф схемы, содержащий узлы a, b, c, d, e и ветви с номерами 1 – 8.
Учитывая структуру ветвей, изобразить схему цепи.
Полагая источники ЭДС и тока в полученной схеме постоянными во времени, изобразить схему, достаточную для расчета токов ветвей и напряжения на источнике тока.
Для полученной схемы:
1. Моделированием в системе ElectronicsWorkbench определить сопротивление в пассивной цепи относительно узлов присоединения ветви с R6.
2. Не преобразовывая схемы, составить систему уравнений по законам Кирхгофа для расчета токов всех ветвей схемы и напряжения на источнике тока и рассчитать их.
3. Преобразовать схему до трех контуров и для преобразованной схемы определить:
3.1. Токи ветвей схемы методом контурных токов.
3.2. Токи ветвей схемы методом узловых потенциалов.
3.3. Записать уравнение баланса мощностей и подсчитать мощности источников энергии и нагрузок.
3.4. Определить напряжение на источнике тока методом наложения.
3.5. Представить схему относительно ветви с источником тока активным эквивалентным источником, определить его параметры и найти напряжение на источнике тока.
|
|
3.6. Моделированием в системе ElectronicsWorkbench убедить в правильности определения параметров эквивалентного источника (RГи EГ)и напряжения на источнике тока.
4. Для внешнего контура исходной схемы рассчитать и построить потенциальную диаграмму.
5. По результатам расчетов составить таблицу и дать краткую характеристику использованным методам.
| №Варианта | Номера ветвей | |||||||
| bc | Da | ca | ab | be | ce | de | cd |
Таблица 1.
| № варианта | R, Ом | E1,В | E2, В | J, А |
| 0,6 |
Таблица 2.
Изобразим граф схемы (рис. 1а) и схему цепи (рис. 1б).
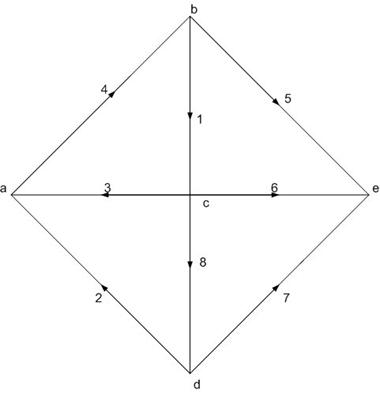
Рис. 1а Граф схемы
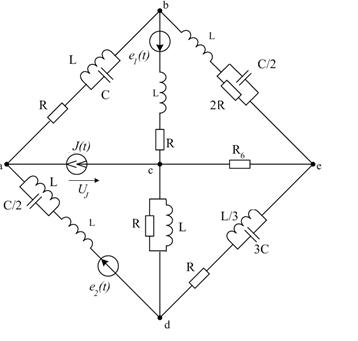
Рис. 1б Схема цепи
По условию задания ЭДС и ток постоянные во времени, поэтому для расчета токов ветвей достаточно изобразить схему, состоящую из резисторов и источников энергии (рис. 2). Ее легко обосновать, используя взаимосвязи между токами и напряжениями на индуктивном 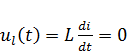 и емкостном
и емкостном 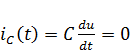 элементах.
элементах.
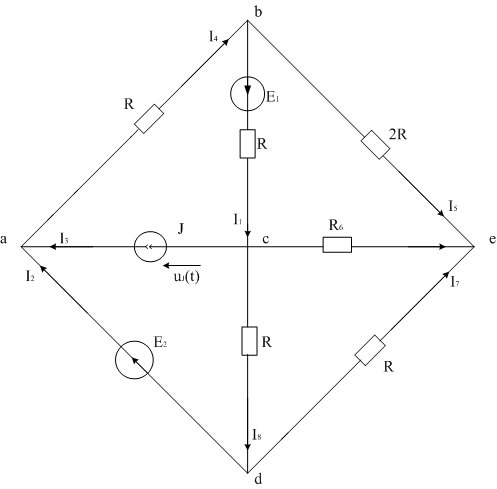
Рис. 2
ЗАДАНИЕ 1.
Смоделировав в системе ElectronicsWorkbench пассивную цепь и подставив мультиметр вместо сопротивления R6, получим следующее (рис. 3).
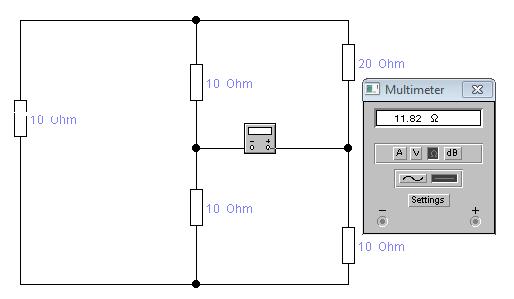
Рис.3
По условию задания необходимо принять значение сопротивления R6равным 0,4 – 0,8 от значения сопротивления пассивной цепи. По согласованию с преподавателем возьмем значение 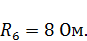
ЗАДАНИЕ 2.
Определим токи всех ветвей схемы и напряжение на источнике тока путем составления системы уравнений по законам Кирхгофа.
В полученной схеме (рис. 2)5 узлов. Следовательно, по первому закону Кирхгофа для данной цепи необходима запись 4 уравнений. Выберем в качестве опорного узла, для которого уравнение не записывается, узел e. Тогда согласно первому закону Кирхгофа:
|
|
| Для узла a | 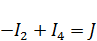 ; ;
|
| Для узла b | 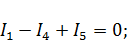
|
| Для узла c | 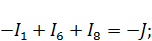
|
| Для узла d | 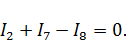
|
Недостающие уравнения запишем по второму закону Кирхгофа для главных контуров. В имеющейся схеме (рис. 2) 8 ветвей с неизвестными напряжениями или токами. Следовательно, необходима запись 4 уравнений, причем, необходимо выбрать направление обхода контуров. Примем за положительное направление обхода контуров движение по часовой стрелке. Тогда по второму закону Кирхгофа:
| Для контура 1 | 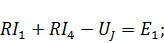
|
| Для контура 2 | 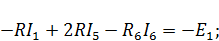
|
| Для контура 3 | 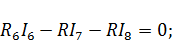
|
| Для контура 4 | 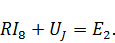
|
Для расчета значений токов воспользуемся системой Mathcad.

Отсюда, значения искомых токов и напряжения равны:
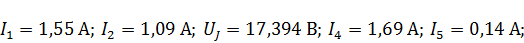
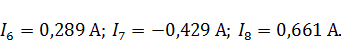
ЗАДАНИЕ 3.
Преобразуем исходную схему (рис. 2)в эквивалентную трехконтурную (рис. 4).
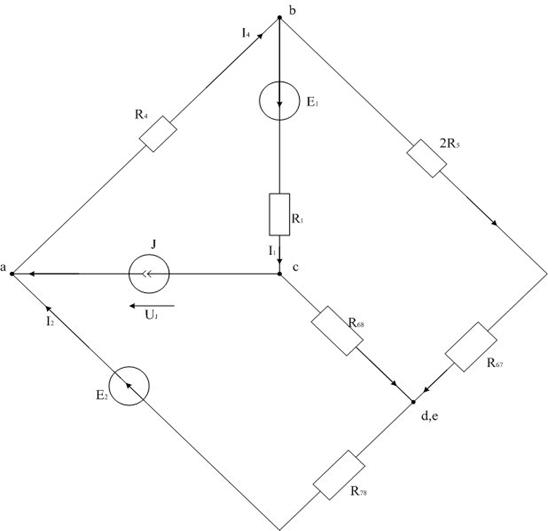
Рис. 4
В преобразованной схеме найдем новые сопротивления 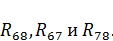
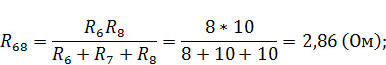
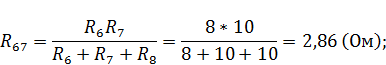
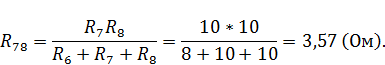
ЗАДАНИЕ 3.1.
Выберем в трехконтурной схеме направления контурных токов 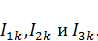 Причем, возьмем контур 1, как показано на рисунке 5, то есть в контур 1 входят источник тока, оба источника ЭДС, а также сопротивления
Причем, возьмем контур 1, как показано на рисунке 5, то есть в контур 1 входят источник тока, оба источника ЭДС, а также сопротивления 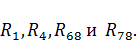
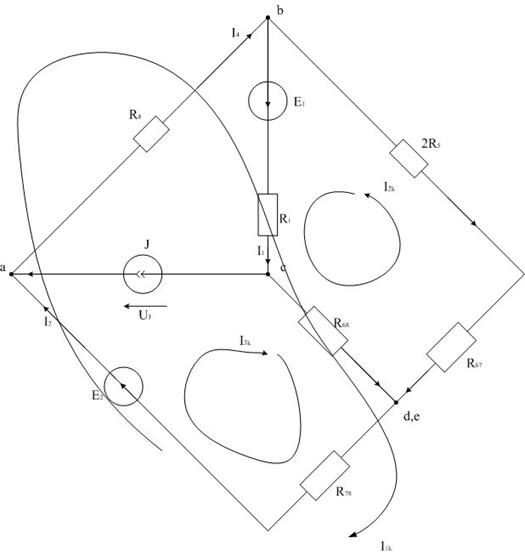
Рис. 5
Примем ток контура 3 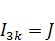 и выразим токи ветвей через контурные токи. Тогда
и выразим токи ветвей через контурные токи. Тогда
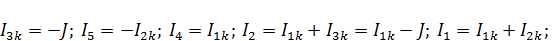
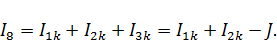
Также для контуров 1 и 2 запишем уравнения:
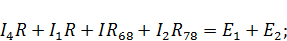
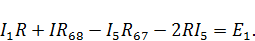
После подстановки значений токов получаем:
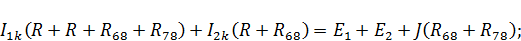
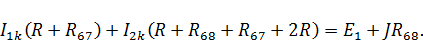
Найдем напряжение источника тока из контура 3:
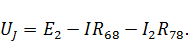
Для расчета контурных токов, токов ветвей, и напряжения на источнике тока воспользуемся системой Mathcad.

Отсюда 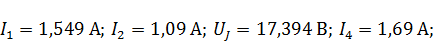
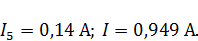
ЗАДАНИЕ 3.2.
Рассчитаем трехконтурную схему (рис. 6) методом узловых потенциалов. Примем потенциал узла d,e равным 0, то есть 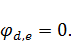
|
|
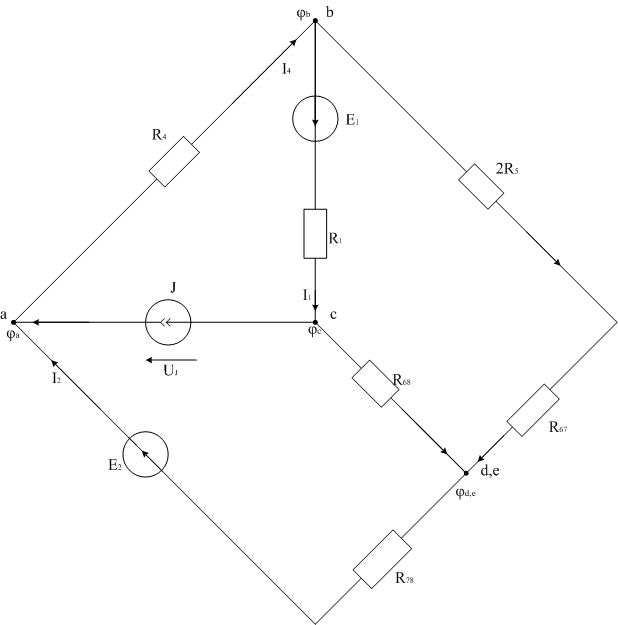
Рис. 6
Так как 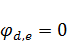 , то уравнения для потенциалов оставшихся узлов записываются следующим образом:
, то уравнения для потенциалов оставшихся узлов записываются следующим образом:
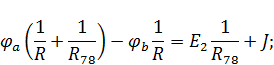
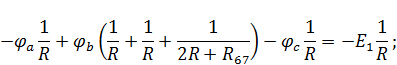
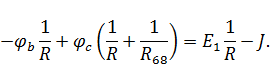
Найденные потенциалы однозначно определяют токи ветвей. Для рассматриваемой схемы (рис. 6):
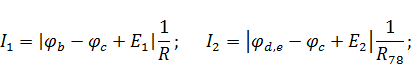
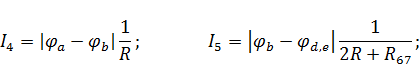
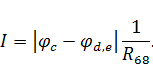
Для расчета узловых потенциалов и токов ветвей воспользуемся системой Mathcad.

Отсюда 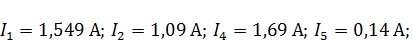
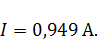
ЗАДАНИЕ 3.3.
Запишем для трехконтурной схемы (рис. 4) уравнениемощности источников и мощности потребителей:
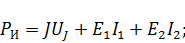
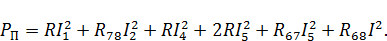
Рассчитаем также допустимую относительную погрешность расчета:
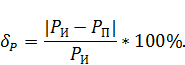
Для расчета мощности источников и мощности потребителей воспользуемся системой Mathcad.

Как видно из расчета в рассматриваемой схеме наблюдается баланс мощностей, так как допустимая относительная погрешность стремится к нулю: 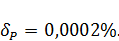
ЗАДАНИЕ 3.4.
Составим из трехконтурной схемы (рис. 4) подсхемы (рис. 7а, 7б, 7в), используемые в методе наложения, которые в дальнейшем будут преобразованы для упрощения расчетов.
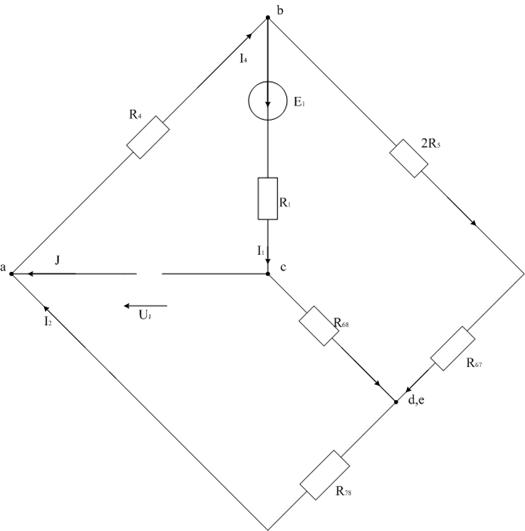
Рис. 7а
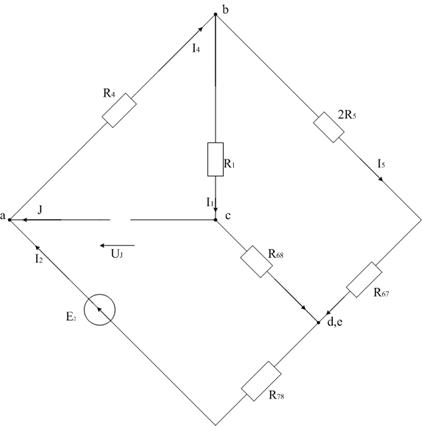
Рис. 7б
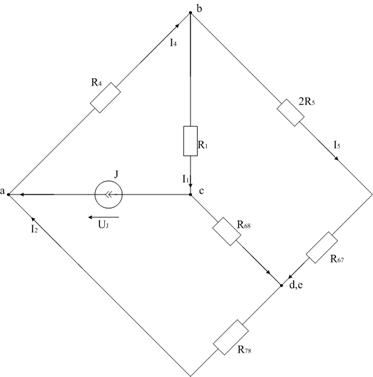
Рис. 7в
1) Рассмотрим случай, когда в схеме присутствует только источник ЭДС Е1 (рис. 7а) и рассчитаем напряжение UJ в этом случае. Путем преобразований приходим к следующей схеме (рис. 8а).
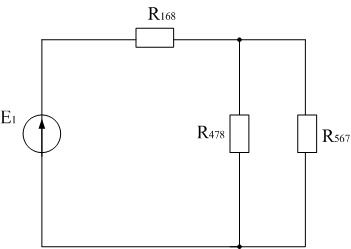
Рис. 8а
Рассчитаем полученные в данном случае сопротивления:
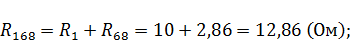
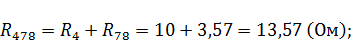
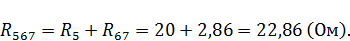
Рассчитаем токи ветвей данной схемы:
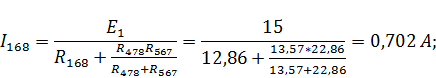
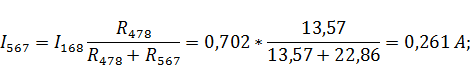
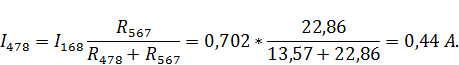
Рассчитаем напряжение в контуре, обозначенном на рисунке 7а:
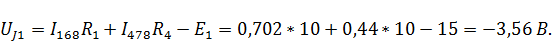
2) Рассмотрим случай, когда в схеме присутствует только источник ЭДС Е2 (рис. 7б) и рассчитаем напряжение UJ в этом случае. Путем преобразований приходим к следующей схеме (рис. 8б).
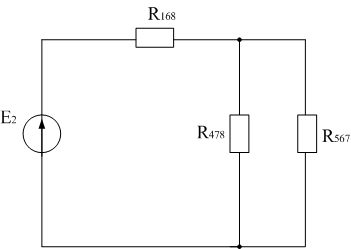
Рис. 8б
Рассчитаем полученные в данном случае сопротивления:
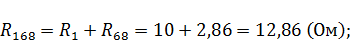
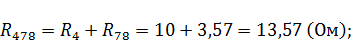
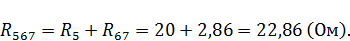
Рассчитаем токи ветвей данной схемы:
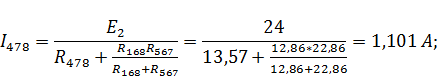
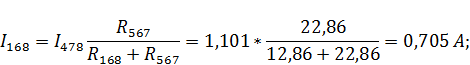
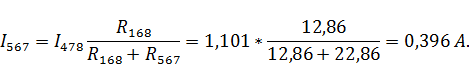
Рассчитаем напряжение в контуре, обозначенном на рисунке 7б:
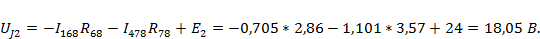
3) Рассмотрим случай, когда в схеме присутствует только источник тока J (рис. 7в) и рассчитаем напряжение UJ в этом случае. Путем преобразований приходим к следующей схеме (рис. 8в).
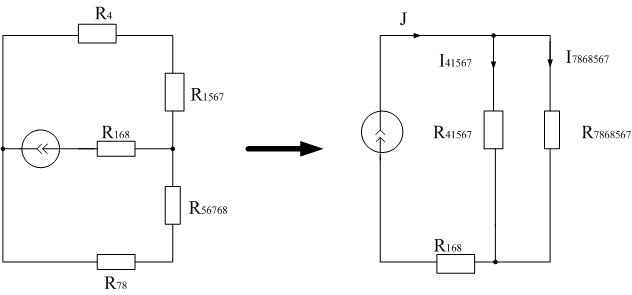
Рис. 8в
Рассчитаем полученные в данном случае сопротивления:
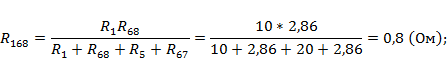
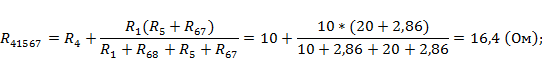
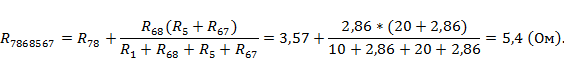
Рассчитаем токи ветви данной схемы:
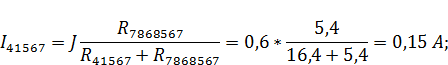
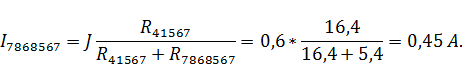
Рассчитаем напряжение в контуре, обозначенном на рисунке 7в:
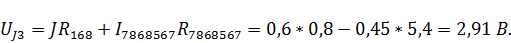
Согласно методу наложения 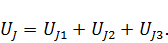 Следовательно,
Следовательно, 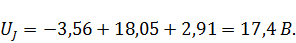
Рассчитаем погрешность вычисления:
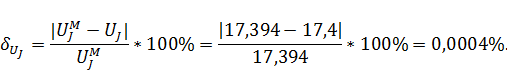
ЗАДАНИЕ 3.5.
Рассмотрим схему с исключенным источником тока (рис. 9).
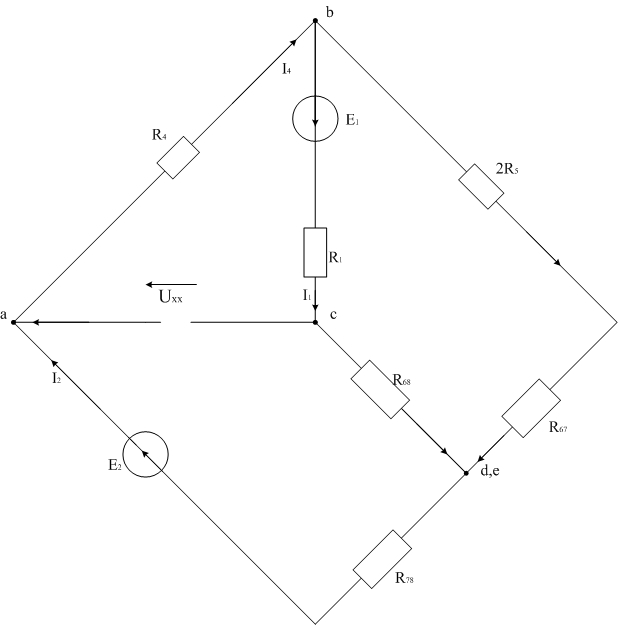
Рис. 9
Из данной схемы можно рассчитать напряжение холостого хода и ЭДС эквивалентного генератора:
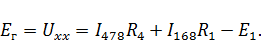
Для численного значения необходимо найти токи 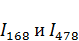 . Для этого преобразуем схему, изображенную на рисунке 9, к следующему виду (рис. 10):
. Для этого преобразуем схему, изображенную на рисунке 9, к следующему виду (рис. 10):
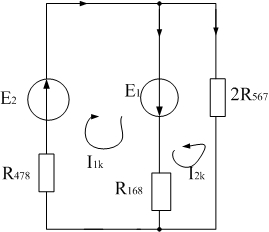
Рис. 10
Из данной схемы рассчитаем токи 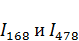 методом контурных токов.
методом контурных токов.
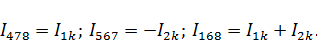
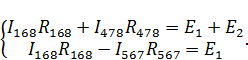
В результате преобразований получим:
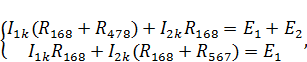
причем в данной формуле 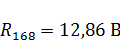 , вычисление которого подробно расписано в методе наложения при расчетах схем, изображенных на рисунках 8а и 8б.
, вычисление которого подробно расписано в методе наложения при расчетах схем, изображенных на рисунках 8а и 8б.
Для нахождения сопротивления генератора воспользуемся схемой, изображенной на рисунке 8в.
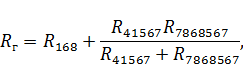
причем в данной формуле 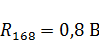 , вычисление которого подробно расписано в методе наложения при расчете схемы, изображенной на рисунке 8в.
, вычисление которого подробно расписано в методе наложения при расчете схемы, изображенной на рисунке 8в.
Представим трехконтурную схему (рис. 4) в виде схемы с эквивалентным источником (рис. 11).
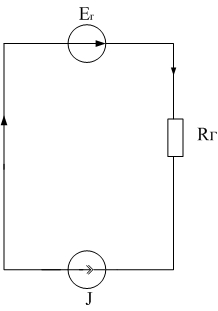
Рис. 11
Из данной схемы видно, что искомое напряжение 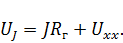
Для расчета искомых величин воспользуемся системой Mathcad.

ЗАДАНИЕ 3.6.
Смоделируем схему, изображенную на рисунке 11 в системе ElectronicsWorkbench и подключим вольтметр параллельно источнику тока, чтобы удостовериться в правильности расчетов (рис. 12).
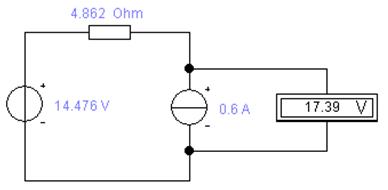
Рис. 12
Показания вольтметра в смоделированной схеме совпадают с рассчитанным значением, что свидетельствует о верности вычисления характеристик эквивалентного источника.
ЗАДАНИЕ 4.
Для построения потенциальной диаграммы рассмотрим внешний контур исходной схемы (рис. 13).
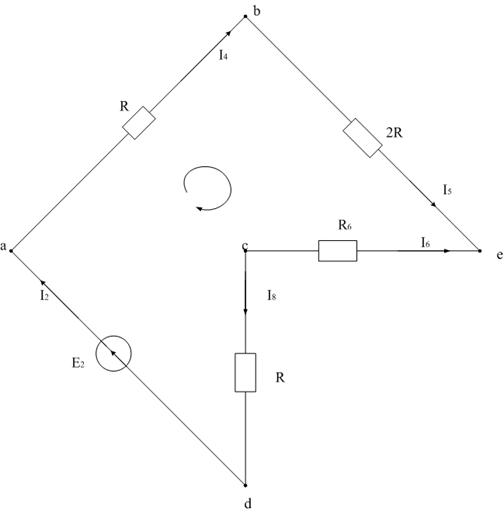
Рис. 13
Примем потенциал узла e равным нулю. Тогда при обходе контура по часовой стрелке имеем:
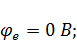
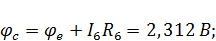
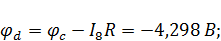
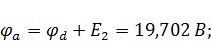
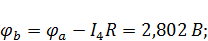
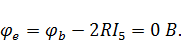
Потенциальная диаграмма – графическое изображение второго закона Кирхгофа, который гласит, что алгебраическая сумма напряжений в контуре равна нулю, на плоскости. Именно это и наблюдается в данном случае и построенная диаграмма (рис. 14) начинается и заканчивается при нулевом значении потенциала.
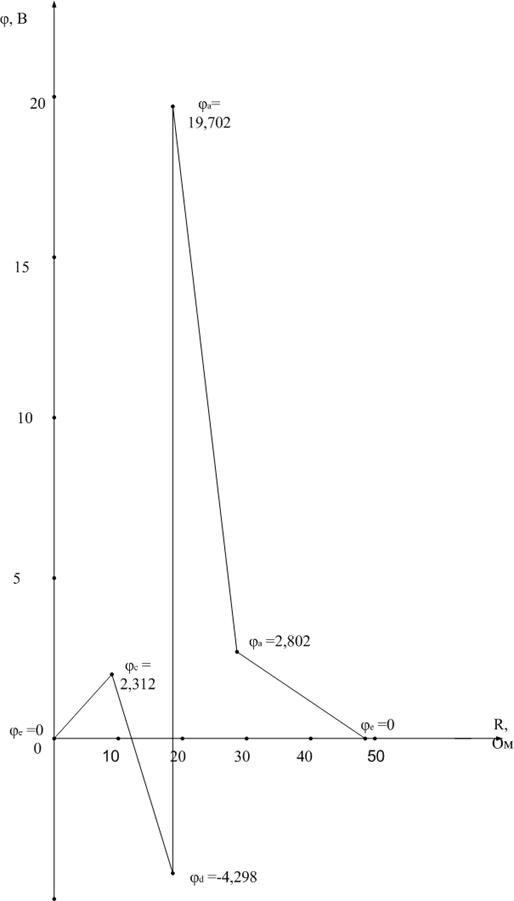
Рис. 14.
ЗАДАНИЕ 5.
| Рассчитанные значения | Использованные методы расчета | |||
| Метод уравнений Кирхгофа | Метод контурных токов | Метод узловых потенциалов | Метод эквивалентного источника | |
| I1, A | 1,55 | 1,549 | 1,549 | - |
| I2, A | 1,09 | 1,09 | 1,09 | - |
| UJ, B | 17,394 | 17,394 | - | 17,4 |
| I4, A | 1,69 | 1,69 | 1,69 | - |
| I5, A | 0,14 | 0,14 | 0,14 | - |
| I6, A | 0,289 | - | - | - |
| I7, A | 0,429 | - | - | - |
| I8, A | 0,661 | - | - | - |
Таблица3
Из таблицы значений можно сделать вывод о равносильности использованных в данной расчетно-графической работе методов расчета, так как значения одних и тех же величин, рассчитанных различными методами, совпадают. Иногда идеального совпадения добиться не удается вследствие наличия погрешности вычисления.
Краткий анализ использованных методов расчета.
· Метод уравнений Кирхгофа применим к любой цепи, так как в его основу положены законы Кирхгофа, и является базовым. Этот метод удобен для полного расчета всех токов ветвей и напряжений, если таковых несколько, но является несколько громоздким и трудоемким в силу, того, что без специальных программ достаточно трудно рассчитывать матрицы.
· Метод контурных токов применяется в случае наличия небольшого количества контуров и источника тока в схеме, так как в контуре с источником тока контурный ток равен току источника тока, и уравнение для него не записывается. Этот метод также удобен для полного расчета всех токов цепи, но не рекомендуем к применению при наличии большого числа контуров.
· Метод узловых потенциалов применяется в случае наличия небольшого количества узлов, так как один из узлов принимается в качестве опорного и его потенциал при этом равен нулю. И, следовательно, чем меньше узлов в схеме, тем меньше уравнений в системе.
· Метод эквивалентного источника позволяет представить абсолютно любую цепь в виде эквивалентного источника ЭДС и эквивалентного сопротивления. Этот метод позволяет найти ток или напряжение лишь в одной ветви, что не является удобным для расчета всех токов цепи, но от этого метод не теряет своих полезных качеств.