МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГФБОУ ВПО РЫБИНСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. А. СОЛОВЬЕВА
КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ
| УТВЕРЖДЕНО на заседании методического семинара кафедры ОиТФ «» 2 013 г. Зав.каф. Пиралишвили Ш.А. | |
Лаборатория «Физические основы механики»
ЛАБОРАТОРНАЯ РАБОТА № ФМ-5 «А»
ИЗУЧЕНИЕ УПРУГОГО УДАРА
| Руководство переработано: | |
| к. т. н., доц. Каляевой Н. А. | |
| Рецензент: к. п. н., доцент Попкова Е. А. | |
| |
Рыбинск 2013
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
В механике под ударом понимают кратковременное взаимодействие двух или нескольких тел, возникающее в результате их соприкосновения и приводящее к значительному изменению состояния движения. Явление удара протекает обычно тысячные, и даже миллионные доли секунды. Время, в течение которого взаимодействуют тела при ударе, называется временем соударения. Оно зависит от упругих свойств материала, из которого изготовлены взаимодействующие тела, их относительной скорости в момент начала удара и от их массы.
При ударе тела деформируются, и в месте контакта возникают весьма значительные ударные силы F уд, величина которых соответствует 104 –106 Н. Для системы соударяющихся тел эти силы являются внутренними и не изменяют общего импульса системы, т.е. такая система является замкнутой. Следствием удара могут быть остаточные деформации, звуковые колебания, нагревание тел, изменение механических свойств их материалов, а при больших скоростях соударения, бо/льших так называемых критических, наблюдается разрушение тел в месте удара. Характер протекания удара существенно зависит от модуля упругости, твердости, вязкости и других свойств материала соударяющихся тел, размеров и массы тел. Знание времени соударения позволяет производить расчет возникающих при ударе сил, что очень важно при решении многих технических задач.
Во время удара кинетическая энергия ударяющего тела переходит в энергию упругой деформации. При этом возникают упругие силы, возрастающие с увеличением деформации, направленные противоположно относительным скоростям соударяющихся тел. Возникающие в результате действия упругих сил ускорения уменьшают скорости тел до тех пор, пока они не станут одинаковыми, или, что тоже самое, пока относительная скорость тел не станет равной нулю. С момента, когда относительная скорость стала равной нулю, начинается частичное или полное восстановление деформации. Силы, продолжая действовать в прежнем направлении, сообщают теперь взаимодействующим телам положительные ускорения, а, следовательно, скорости взаимодействующих тел возрастают по абсолютной величине, направление же их меняется на противоположное.
Если направление движения соударяющихся тел в момент их соприкосновения совпадает с прямой, соединяющей центры масс тел, то такой удар называют центральным.
Различают два предельных случая удара – абсолютно упругий и абсолютно неупругий.
Удар называется абсолютно упругим, если механическая энергия тел не переходит в другие, немеханические виды энергии. В этом случае кинетическая энергия соударяющихся тел переходит полностью или частично в потенциальную энергию упругой деформации, после чего тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию и тела разлетаются со скоростями, величина и направление которых определяются двумя условиями – сохранением полной механической энергии и сохранением полного импульса системы тел.
Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает; кинетическая энергия тел полностью или частично переходит во внутреннюю энергию. После удара столкнувшиеся тела либо движутся вместе с одинаковой скоростью, либо покоятся. При таком ударе выполняется закон сохранения импульса, однако закон сохранения механической энергии не выполняется, т.к. часть механической энергии переходит во внутреннюю. В этом случае выполняется более общий закон сохранения энергии – механической и внутренней. В реальных ситуациях всегда имеет место некоторая комбинация обоих предельных случаев.
Для характеристики удара вводят понятие коэффициента восстановления относительной скорости при ударе k, который характеризует степень неупругости удара:
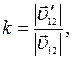 (1)
(1)
где 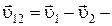 относительная скорость шаров до удара,
относительная скорость шаров до удара,
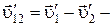 относительная скорость шаров после удара.
относительная скорость шаров после удара.
Для абсолютно упругого удара k = 1, для абсолютно неупругого удара k = 0, во всех остальных случаях (реальный удар) 0 < k < 1 (например, для стальных шаров k≈0,56, для шаров из слоновой кости k≈0,89, для свинца k≈0).
Помимо коэффициента восстановления относительной скорости вводят также коэффициент восстановления энергии ε, определяемый выражением:
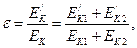 (2)
(2)
где 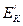 =
= 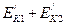 - суммарная кинетическиа энергия тел после удара;
- суммарная кинетическиа энергия тел после удара;
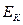 =
= 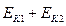 - суммарная кинетическиа энергия тел до удара.
- суммарная кинетическиа энергия тел до удара.
Величину средней силы удара можно найти на основании второго закона Ньютона:
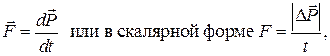 (3)
(3)
где 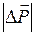 - модуль изменения импульса одного из тел в результате удара, t – время удара.
- модуль изменения импульса одного из тел в результате удара, t – время удара.
 Рис. 1
Рис. 1
|
Рассмотрим абсолютно упругий центральный прямой удар двух шаров с массами 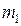 и
и 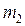 и скоростями
и скоростями  и
и 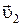 соответственно (рис.1а).
соответственно (рис.1а).
Согласно закону сохранения импульса, имеем:
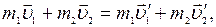 (4)
(4)
где 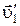 и
и 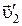 – скорости шаров после соударения (рис.1б).
– скорости шаров после соударения (рис.1б).
Запишем выражение закона сохранения энергии:
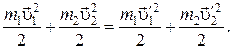 (5)
(5)
Перепишем уравнение (4) в виде:
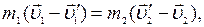 (6)
(6)
а уравнение (5) в виде:
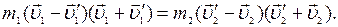 (7)
(7)
Сопоставив (6) и (7), можно заключить, что
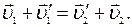 (8)
(8)
Умножив (8) на m 2 и вычтя результат из (6), а затем, умножив (8) на m 1 и сложив результат с (6), получим скорости шаров после удара:
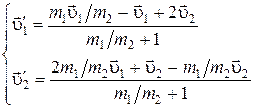 . (9)
. (9)
Для численных расчетов нужно спроектировать соотношения (9) на ось, вдоль которой движутся шары.
Рассмотрим упругий удар шара массой 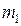 о неподвижную стенку. Масса стенки
о неподвижную стенку. Масса стенки 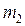 >>
>> 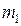 , и поэтому
, и поэтому 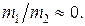
Тогда
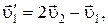
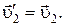
При покоящейся стенке 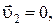 и поэтому
и поэтому
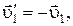
– скорость стенки остается неизменной, скорость же шара меняет свое направление на противоположное.
Рассмотрим абсолютно неупругий удар. Продемонстрировать такой удар можно с помощью шаров из пластилина (глины), движущихся навстречу друг другу (рис. 2).
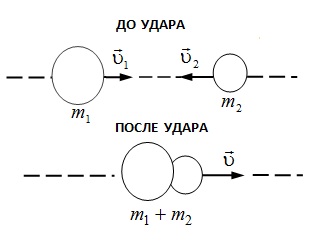
Рис.2
Если массы шаров т 1 и т 2, их скорости до удара 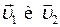 , то, используя закон сохранения импульса, можно записать
, то, используя закон сохранения импульса, можно записать
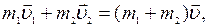
где 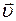 — скорость движения шаров после удара. Тогда
— скорость движения шаров после удара. Тогда
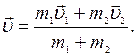 (10)
(10)
Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае, если массы шаров равны (т 1= т 2), то
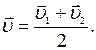
Выясним, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие не от самих деформаций, а от их скоростей, то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения механической энергии не должен соблюдаться. Вследствие деформации происходит «потеря» кинетической энергии, перешедшая в тепловую или другие формы энергии. Эту «потерю» можно определить по разности кинетической энергии тел до и после удара:
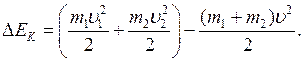
Используя (10), получаем
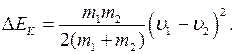
Если ударяемое тело было первоначально неподвижно (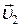 = 0), то
= 0), то
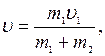
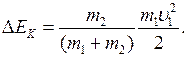
Когда m 2>> m 1 (масса неподвижного тела очень большая), то 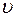 <<
<< 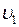 и почти вся кинетическая энергия тела при ударе переходит в другие формы энергии. Поэтому, например, для получения значительной деформации наковальня должна быть массивнее молотка. Наоборот, при забивании гвоздей в стену масса молотка должна быть гораздо большей (m 1>> m 2 ), тогда
и почти вся кинетическая энергия тела при ударе переходит в другие формы энергии. Поэтому, например, для получения значительной деформации наковальня должна быть массивнее молотка. Наоборот, при забивании гвоздей в стену масса молотка должна быть гораздо большей (m 1>> m 2 ), тогда 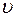 ≈
≈ 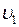 и практически вся энергия затрачивается на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.
и практически вся энергия затрачивается на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.
Абсолютно неупругий удар — пример того, как происходит «потеря» механической энергии под действием диссипативных сил.