Через прямую l провести плоскость l, перпендикулярную к заданной плоскости b(hÇf).

Решение: Через произвольную точку М на прямой l проведем прямую n, перпендикулярную к заданной плоскости b(hÇf). Условие перпендикулярности согласно. Пересекающиеся прямые l и n и определят искомую плоскость l(nÇl).
№16 Условие параллельности прямой и плоскости.
Из стереометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости.
Признак перпендикулярности прямой и плоскости на чертеже.
Если в пространстве прямая перпендикулярна плоскости, то на чертеже горизонтальная проекция прямой должна быть перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция - к фронтальной проекции фронтали этой плоскости


№17 Построение точки пересечения прямой и плоскости.
Прямая называется пересекающей плоскость, если она имеет с ней только одну общую точку. Рассмотрим различные случаи пересечения прямой и плоскости.
Частные случаи:
Пример 1. Прямая – проецирующая, плоскость – частного положения.
На КЧ необходимо построить проекции точки пересечения прямой с плоскостью и определить видимость этой прямой относительно горизонтальной и фронтальной плоскостей проекций.
Точка К должна одновременно принадлежать и прямой, и плоскости.
1) Горизонтальную проекцию точки пересечения находим из условия принадлежности ее прямой i. Так как все точки, лежащие на горизонтально-проецирующей прямой, совпадают с ее следом: К1 º i1.
2) Определение фронтальной проекции точки пересечения сводится к задаче на принадлежность точки К плоскости 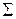 :
:
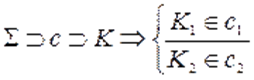 .
.

Пример 2. Прямая – общего положения, плоскость – проецирующая.

№18 Условие перпендикулярности прямой и плоскости. Построение перпендикуляра к плоскости на эпюре.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. При построении перпендикуляра из множества прямых принадлежащих плоскости, выбирают прямые уровня - горизонталь и фронталь. В этом случае горизонтальную проекцию перпендикуляра проводят перпендикулярно горизонтали, а фронтальную -перпендикулярно фронтали.

Показано построение перпендикуляра к плоскости, заданной треугольником АВС, из точки К. Для этого сначала проводим горизонталь и фронталь в плоскости. Затем из фронтальной проекции точки К проводим перпендикуляр к фронтальной проекции фронтали, а из горизонтальной проекции точки – перпендикуляр к горизонтальной проекции горизонтали. Затем строим точку пересечения данного перпендикуляра с плоскостью при помощи вспомогательной секущей плоскости Σ. Искомая точка – F. Таким образом, полученный отрезок КF является перпендикуляром к плоскости АВС.
№19 Взаимно перпендикулярные плоскости.
Частный случаем пересечения плоскостей являются взаимно перпендикулярные плоскости.
Известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей, перпендикулярных данной плоскости a(h,f). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a. Для того, чтобы через точку А провести плоскость, перпендикулярную плоскости a(h, f),необходимо из точки А провести прямую n, перпендикулярную плоскости a(h, f), (горизонтальная проекция n1 перпендикулярна горизонтальной проекции горизонтали h1, фронтальная проекция n2 перпендикулярна фронтальной проекции фронтали f2). Любая плоскость, проходящая через прямую n будет перпендикулярна плоскости a(h, f), поэтому для задания плоскости через точку А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми (m, n),будет перпендикулярна плоскости a(h, f)

| 
|
№20 Построение линии пересечения плоскостей. Привести примеры.
На рисунке даны две плоскости. Одна задана треугольником АВС, а другая двумя пересекающимися прямыми l и m. Эти плоскости параллельны, т.к прямая l // ВС, а m // АС.
Прямая линии пересечения двух плоскостей определяется двумя точками, каждая из которых принадлежит обеим плоскостям. Для того чтобы определить общую точку, принадлежащую обеим плоскостям, вводят вспомогательную плоскость. Затем определяют линии пересечения вспомогательной плоскости и двух данных. Точка пересечения этих линий будет общей точкой плоскостей.
На практике обычно пользуются другим способом - находят точки пересечения двух прямых, принадлежащих одной плоскости с другой плоскостью, и через них проводят линию пересечения плоскостей. Возьмем для примера две плоскости в виде треугольников и построим линию их пересечения таким способом. На рисунке даны две непрозрачные пластины АВС и EFG. Первая вспомогательная секущая плоскость S берется по стороне EG. Она пересекает плоскость треугольника АВС по линии 12. Строим горизонтальную проекцию линии 12 и находим точку пересечения ее со стороной EG.

Получаем точку М – горизонтальную проекцию точки пересечения. Вторая точка К находится аналогично, путем введения вспомогательной секущей плоскости S¢ по стороне АВ. Затем определяется видимость плоскостей при помощи конкурирующих точек. Для того чтобы придать чертежу наглядность, одну из пластин можно заштриховать.
№21 Метод замены плоскостей проекции.
Изменение взаимного положения изучаемого объекта и плоскостей проекций достигается путем замены одной из плоскостей П1 или П2 новой плоскостями П4. Новая плоскость всегда выбирается перпендикулярно оставшейся плоскости проекций.
Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.
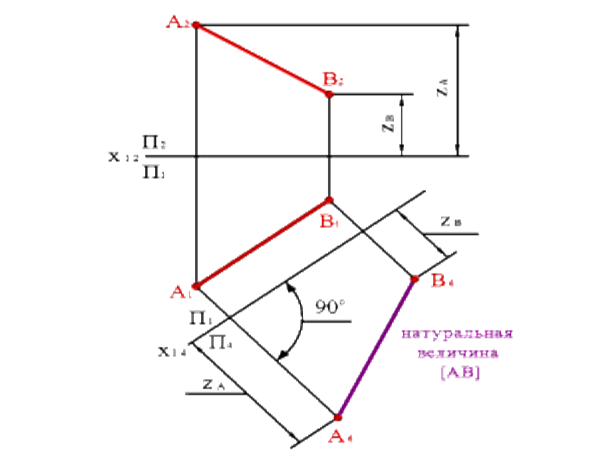
Задача 1: Определить натуральную величину отрезка АВ прямой общего положений. Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.
Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4, причем в новой системе плоскостей проекция отрезка А4 В4 будет натуральной величиной отрезка АВ.
| ||
№22 Сущность метода вращения вокруг осей, перпендикулярных плоскостям проекций.
Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линии уровня или проецирующие прямые.
Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.
1. Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
2. При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
3. При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.
Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.
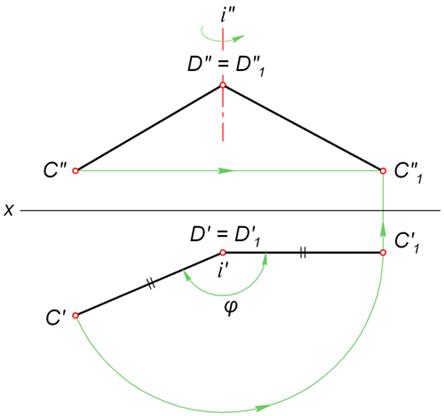
При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C' переместим по дуге окружности радиусом C'D' в положение C'1 так, чтобы выполнялось условие C'1D'1 || X. Для нахождения точки C''1 из C'' проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C'1.
№23 Пересечение многогранников с плоскостью.
Данная задача относится к задаче на принадлежность: только не точки, а сечения.
Геометрическая фигура, полученная в результате пересечения многогранника плоскостью, называется сечением многогранника.
Сечение представляет собой один или несколько многоугольников. Графические приемы построения сечений сводятся к многократному решению задачи на пересечение ребер многогранника с плоскостью сечений. Задача решается просто, если секущая плоскость сечения занимает проецирующее положение. В этом случае задача графического построения многогранника проецирующей плоскостью сводится к многократному решению задачи на принадлежность точек ребру. Точки 1,2,3 принадлежат ребрам SA,SB,SC многогранника ABCS.

№24 Пересечение прямой линии с поверхностью многогранников.
В общем случае алгоритм определения точек пересечения (точек входа и выхода) прямой с поверхностью многогранника аналогичен алгоритму определения точки пересечения прямой с плоскостью и состоит в следующем:
1) через данную прямую проводим вспомогательную плоскость;
2) строим сечение заданной поверхности с вспомогательной плоскостью;
3) определяем искомые точки как точки пересечения данной прямой с ломаной линией, ограничивающей контур сечения.

Пример. Определить точки пересечения прямой l с поверхностью наклонной призмы.
Решение. Расчет статически неопределимой фермы Задачи по строительной механике
1) Заключаем прямую l в горизонтально-проецирующую плоскость Q (Q').
2) Определяем сечение (1-2-3) призмы с плоскостью Q.
Для этого сначала определяем точки 1,2,3 на горизонтальной проекции как точки пересечения ребер с вырожденной проекцией Q', а затем по линиям связи определяем фронтальные проекции 1",2",3".
3). Определяем точки K1 и K2 пересечения проекции l '' со стороной треугольника 1'',2'',3''. Горизонтальные проекции K'1 и K'2 искомых точек лежат на горизонтальной проекции l ' прямой l.
№25 Пересечение поверхностей вращения плоскостью.
Линиями пересечения поверхностей вращения чаще всего бывают пространственные кривые, но могут быть плоские кривые и даже прямые линии.
В общем случае для построения линии пересечения двух поверхностей вращения применяются вспомогательные плоскости. В качестве таких плоскостей чаще всего используются плоскости, параллельные одной из плоскостей проекций. Положение их выбирают таким, чтобы они пересекали заданные поверхности по простейшим линиям — прямым или окружностям.
Рассмотрим построение линии пересечения двух цилиндров, образующие которых занимают проецирующее положение. В этом случае две проекции линии пересечения строить не надо, так как профильная проекция совпадает с проекцией боковой поверхности малого цилиндра, а горизонтальная проекция — с двумя частями окружности, представляющей собой проекцию боковой поверхности большего цилиндра. Таким образом, остается построить только фронтальную проекцию линии пересечения.
№26 Пересечение прямой линии с поверхностями цилиндра и конуса
Для построения точек пересечения прямой АВ общего положения с поверхностью наклонного кругового цилиндра выберем вспомогательную плоскость, параллельную оси цилиндра. Эта плоскость пересекает цилиндр по прямым — образующим, параллельным оси.

прямая АВ заключена во вспомогательную плоскость, параллельную оси цилиндра, для чего через проекции т', т произвольной точки М на прямой АВ проведены проекции т'п', тп прямой MN, параллельной оси цилиндра. Проекции пересекающихся прямых А В и MN задают на чертеже вспомогательную плоскость;
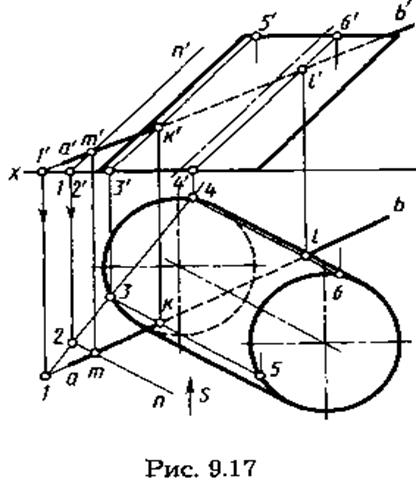
построены проекции 3'5', 3—5 и 4'6', 4— 6 линий пересечения вспомогательной плоскости с поверхностью цилиндра. Для этого построена горизонтальная проекция линии пересечения вспомогательной плоскости с плоскостью основания цилиндра — плоскостью Н, проходящая через проекции 1 и 2, найдены точки с проекциями 3, 4 ее пересечения с окружностью основания цилиндра. Искомые проекции линий пересечения вспомогательной плоскости с поверхностью цилиндра проходят через проекции 3', 3 и 4', 4 параллельно проекциям оси цилиндра — проекции 3'5', 3—5 и 4'6', 4 — 6;
Определены проекции к', к и l', l искомых точек К и L пересечения прямой АВ с поверхностью цилиндра в пересечении проекций 3'5' и 4'6' с а'b' и 3—5 и 4—6сab;
определена видимость для участков прямой АВ с учетом того, что цилиндр непрозрачен. Зоны видимости на фронтальной проекции определены по положению горизонтальных проекций точек 3 и 4 цилиндра. При взгляде по стрелке S очевидно, что точки 3, 5 и соответственно образующая 3—5 видимы, а точки 4, 6 и образующая 4—6 невидимы. Соответственно на фронтальной проекции отрезок а'к' проекции прямой видим. Справа от точки к' прямая до точки l' проходит внутри цилиндра и справа от точки l' закрывается цилиндром, т. е. невидима. На горизонтальной проекции образующие 3—5 и 4—6 видимы, невидимая часть прямой АВ — отрезок kl.
№27 Построение линии пересечения поверхностей с использованием метода секущих плоскостей. Привести пример.
В качестве поверхностей-посредников используют секущие плоскости. Этот способ применяется в тех случаях, когда можно найти в качестве поверхностей-посредников такие плоскости, которые пересекали бы обе заданные поверхности по геометрически простым линиям — окружностям и прямым (рис. 21). Чаще всего в качестве вспомогательных секущих плоскостей выбираются плоскости уровня, то есть плоскости, параллельные плоскостям проекций. Следует отметить, что способ вспомогательных секущих плоскостей применяется во всех случаях, то есть каждая из пересекающихся поверхностей может быть как гранной, так и поверхностью вращения. вращения. 
Определяют на чертеже положения опорных точек кривой пересечения. Фронтальная проекция A2 самой высшей точки кривой пересечения определяется на пересечении главных меридианов пересекающихся поверхностей: для конуса главным меридианом является очерковый треугольник, а для полусферы — очерковая полуокружность во фронтальной плоскости проекций.
№28 Метод сфер. Привести пример.
Еще один метод построения линии пересечения поверхностей вращения – метод сфер. Он применяется в случаях, когда метод секущих плоскостей использовать нецелесообразно – например, когда оси одной или обеих поверхностей вращения расположены так, что при пересечении этих поверхностей с плоскостями, параллельными плоскостям проекций, образуются сложные фигуры. Один из таких случаев – когда оси поверхностей вращения пересекаются в пространстве. Пусть одна из поверхностей – цилиндр, а вторая – тело вращения, образованное кривой 2-го порядка. Оговоримся, что для применения метода сфер необходимо привести чертеж к такому виду, когда оси вращения обеих поверхностей параллельны одной из плоскостей проекций.
№29 Развертка пирамиды и призмы.
Развертка пирамиды. Развертка пирамиды осуществляется в следующем порядке:
а) определяют истинную величину всех ребер пирамиды любым из известных способов. На рис. способом вращения найдена длина боковых ребер и способом замены плоскостей проекций определено основание пирамиды;
б) по найденным трем сторонам строят какую-либо из боковых граней, например SoAoBo, пристраивая к ней следующую SoBoCo, а затем и остальные грани (масштаб развертки уменьшен);
в) достраивают основание пирамиды A0BoCoDo.
Точки, расположенные внутри контура развертки, находятся во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки. Примером первой пары точек на рисунках служат точки Ко, а иллюстрацией второго случая являются точки М и Мо.
Для определения точки Ко на развертке пришлось по ее ортогональным проекциям найти длины отрезков AM (способом замены плоскостей проекций) и SK (способом вращения). Эти отрезки и были использованы затем при построении на развертке сначала прямой SoMo и, наконец, точки Ко.
Развертка призмы. В общем случае развертка призмы выполняется следующим образом. Преобразуют эпюр так, чтобы боковые ребра призмы стали параллельны новой плоскости проекций. Тогда на эту плоскость боковые ребра спроецируются в истинную величину.
№30 Развертка цилиндра и конуса.

Развертка поверхности цилиндра состоит из прямоугольника и двух кругов. Одну сторону прямоугольника берут равной высоте цилиндра, другую — длине окружности основания.
К прямоугольнику, пристраивают два круга, диаметр которых равен диаметру оснований цилиндра.
Развертка поверхности конуса представляет собой плоскую фигуру, состоящую из сектора — развертки боковой поверхности и круга — основания конуса.