Дожимная насосная станция
Задание: спроектировать систему автоматического управления дожимной насосной станцией (ДНС).
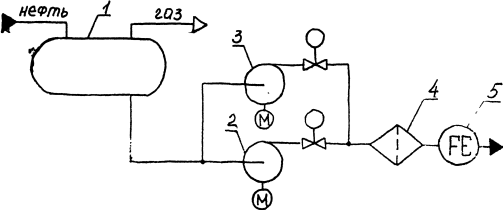
1 – емкость; 2 и 3 – рабочий и резервный насосы с электроприводами; 4 – фильтр; 5 – счетчик нефти
Рисунок 1 – Схема технологического объекта управления
Описание алгоритма управления объектом:
При достижении жидкостью в емкости верхнего уровня включается рабочий насос и начинается откачка, а при достижении жидкостью нижнего уровня насос выключается.
Если по какой-либо причине рабочий насос не справляется с откачкой и жидкость в емкости достигает аварийного уровня, то рабочий насос отключается (во избежание перегрузки по электропитанию), включается резервный насос и подается аварийный сигнал оператору. Резервный насос отключается, также как и рабочий, по нижнему уровню жидкости в емкости.
Предусматривается защита ДНС по верхнему давлению (например, при засорении фильтра) и по нижнему давлению (при неисправностях в насосе, утечках и порывах в трубопроводах) на выходе насосов. При достижении этих давлений с выдержкой времени τ работающий насос отключается и включается аварийная сигнализация.
Этап системного проектирования
Перечень входных и выходных сигналов
Входные сигналы:
Хву – достижение верхнего уровня;
Хну – достижение нижнего уровня;
Хав – достижение аварийного уровня;
Хhp – достижение верхнего (max) давления на выходе насосов;
Xlp – достижение нижнего (min) давления на выходе насосов;
Ysb – сброс;
Z – отсчет времени t.
Выходные сигналы:
Urabnas – вкл/выкл рабочего насоса;
Ureznas – вкл/выкл резервного насоса;
Iopac – аварийный сигнал оператору;
Iac – аварийная сигнализация;
T – запуск таймера.
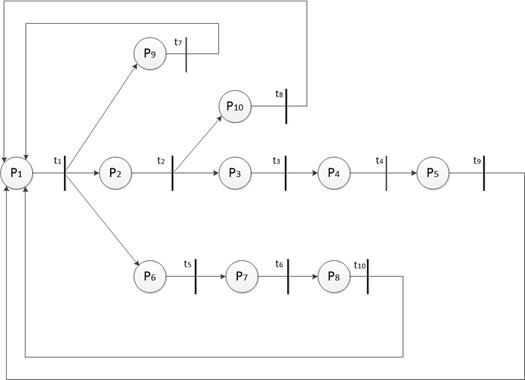
Рисунок 2 – Сеть Петри
Рассмотрим соответствие между входными сигналами и позициями, выходными сигналами и переходами.
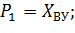
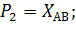
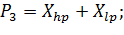
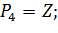
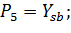
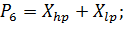
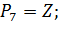
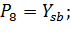
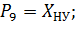
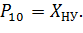
Переходы:
Таблица 1 – Управляющие сигналы переходов
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
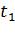
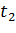
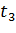
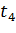
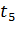
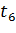
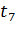
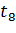
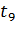
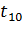
| Urabnas | ||||||||||
| Ureznas | ||||||||||
| Iopac | ||||||||||
| Iac | ||||||||||
| T |
Для сети Петри, изображенной на рисунке 2, синтез конечно-автоматной модели Мура имеет ту же уже затрагиваемую выше сложность, связанную с большим количеством состояний. Поэтому декомпозируем сеть Петри на субсети (рисунок 3).
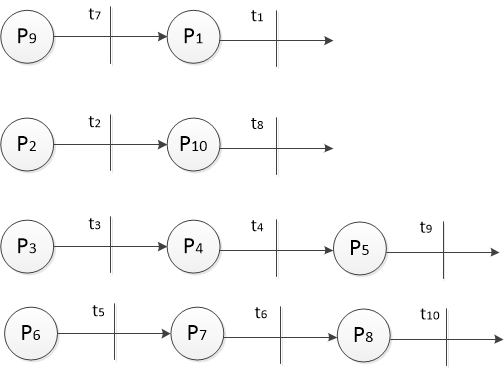
Рисунок 3 – Декомпозиция сети Петри
Проведем синтез конечно-автоматных моделей Мура для первой декомпозированной части (рисунок 3).
| B1˄P9 | P1 | ||
| t7 | |||
| t1 | |||
| t1 |
Введем дополнительные переменные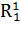 
, 
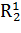. Составим соответствующую таблицу переходов.
|
| |||
|
|
|
|
| |
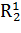
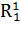
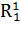
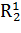
Сформируем таблицы для , .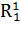
|
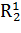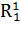
| B1˄P9 | P1 | |
| t7 | |||
| t1 | |||
| t1 |
|
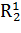
| B1˄P9 | P1 | |
| t7 | |||
| t1 | |||
| t1 |
Получаем:
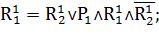
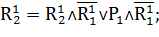
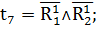
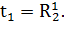
Аналогично получим автоматные модели для остальных подсетей на рисунке 3. Для второй декомпозированной части (рисунок 3):
| B2˄P2 | P10 | ||
| t2 | |||
| t8 | |||
| t8 |
Введем дополнительные переменные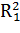 
, 
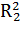. Составим соответствующую таблицу переходов.
|
| |||
|
|
|
|
| |
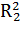
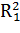
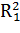
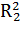
Сформируем таблицы для , .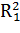
|
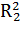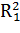
| B2˄P2 | P10 | |
| t2 | |||
| t8 | |||
| t8 |
|
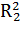
| B2˄P2 | P10 | |
| t2 | |||
| t8 | |||
| t8 |
Получаем:
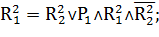
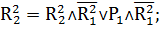
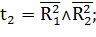
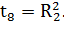
Для третьей декомпозированной части (рисунок 3):
| B3˄P3 | P4 | P5 | ||
| t3 | ||||
| t4 | ||||
| t9 |
Введем дополнительные переменные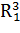 
, 
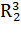. Составим соответствующую таблицу переходов.
|
| |||
|
|
|
|
| |
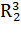
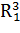
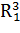
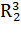
Сформируем таблицы для , .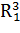
|
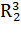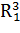
| B3˄P3 | P4 | P5 | |
| t3 | ||||
| t4 | ||||
| t9 |
|
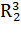
| B3˄P3 | P4 | P5 | |
| t3 | ||||
| t4 | ||||
| t9 |
Получаем:
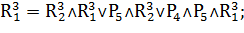
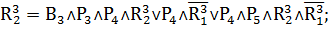
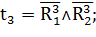
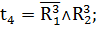
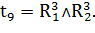
Для четвертой декомпозированной части (рисунок 3, г):
| B4˄P6 | P7 | P8 | ||
| t5 | ||||
| t6 | ||||
| t10 |
Введем дополнительные переменные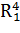 
, 
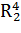. Составим соответствующую таблицу переходов.
|
| |||
|
|
|
|
| |
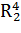
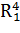
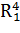
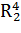
Сформируем таблицы для , .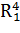
|
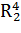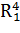
| B4˄P6 | P7 | P8 | |
| t5 | ||||
| t6 | ||||
| t10 |
|
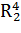
| B4˄P6 | P7 | P8 | |
| t5 | ||||
| t6 | ||||
| t10 |
Получаем:
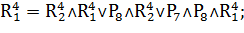
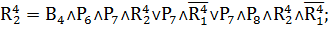
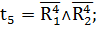
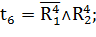
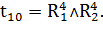
Таким образом:
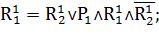
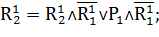
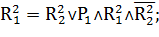
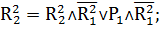
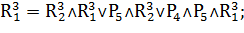
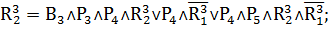
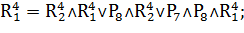
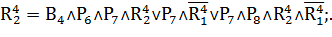
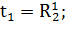
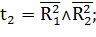
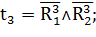
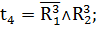
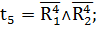
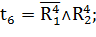
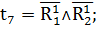
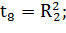
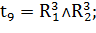
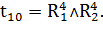
Переходы, формулы которых приведены выше, осуществляют управляющие воздействия в соответствии с таблицей 1.