Задачи для решения в аудитории

2.1. На шахматную доску случайным образом ставят две ладьи, белую и черную. Какова вероятность того, что ладьи не побьют друг друга? Ответ:7/9.

2.2. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради окажутся в клетку? Ответ: .

2.3. Четыре билета на елку распределили по жребию между 15 мальчиками и 12 девочками. Какова вероятность того, что билеты достанутся 2 мальчикам и 2 девочкам? Ответ: .

2.4. Из партии, содержащей 30 изделей, среди которых 5 бракованных наудачу извлекают 5 изделий для контроля. Найдите вероятность того, что среди них хотя бы два изделия являются бракованными. Ответ: 0,63.

2.5. 10 вариантов контрольных работ, написанных каждый на отдельной карточке, перемешиваются и распределяются случайным образом среди 8 студентов, сидящих в одном ряду, причем каждый получает по одному варианту. Какова вероятность того, что варианты 4 и 5 достанутся рядом сидящим студентам? Ответ: .

2.6. С какой вероятностью при подбрасывании трех игральных костей на всех костях выпадет разное количество очков? Ответ. .

2.7. В лотерее 1000 билетов, среди которых 20 выигрышных. Приобретается один билет. Какова вероятность того, что этот билет 1) выигрышный; 2) невыигрышный?

Ответ: 1) ; 2) .

2.8. Андрей и Олег договорились, что если при бросании двух игральных кубиков в сумме выпадет число очков, кратное 5, то выигрывает Андрей, а если в сумме выпадет число, кратное 6, то выигрывает Олег. Справедлива ли эта игра и если нет, что у кого из мальчиков больше шансов выиграть? Ответ: Да.

2.9. Пусть проводится лотерея, и продаются 100 билетов, среди которых 10 выигрышных. Какое наименьшее число билетов нужно купить, чтобы вероятность выигрыша была больше 0,5? Ответ: шесть.

2.10. Гардеробщица выдала одновременно номерки четырем лицам, сдавшим в гардероб свои шляпы. После этого она перепутала все шляпы и повесила их наугад. Найдите вероятности следующих событий:

;

;

;

;

.

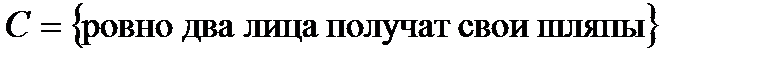Ответ: ; .

2.11. (Задача о совпадениях) Элементы случайным образом переставляются (все 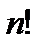перестановок равновероятны). Какова вероятность того, что хотя бы один элемент окажется на своем месте? Найдите .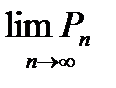

Решение. Пусть событие заключается в том, что -й элемент остался на своем месте, причем . Аналогично, Воспользуемся теоремой о вероятности суммы: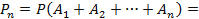

2.12. (Задача о парных днях рождения) При каком минимальном числе студентов в группе вероятность того, что хотя бы два из них родились в один день, больше 0,5? (Годы рождения могут и не совпадать, а каждый год состоит из 365 дней.)

Решение. Пусть - число студентов, и будем считать, что все дни рождения равновероятны. Вычислим вероятность противоположного события . Число способов, благоприятствующих этому событию - это число размещений из 365 по 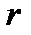. Всего же имеется возможностей распределения дней рождений. То есть . Вероятность интересующего нас события тогда равна .

	0,027	0,117	0,411	0,476	0,507	0, 569	0,707	0,891	0,994

При вероятность по крайней мере одного совпадения равна 0,507>0,5, то есть - наименьшее число, удовлетворяющее условиям задачи. При есть смысл заключать равноправное пари. В случае же вероятность выигрыша 0,706, а вероятность проигрыша - 0,294.

2.13. Две точки независимо друг от друга выбираются на отрезке [0;1]. Найдите вероятности следующих событий:
1) координата первой точки меньше координаты второй точки;
2) сумма координат точке меньше 1,5;
3)разность квадратов координат первой и второй точки больше 0,25.
4) модуль разности координат меньше 1/6.

Ответ: 1) ; 2) ; 3) ; 4) .

2.14. На отрезок длины 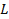числовой оси наудачу поставлена т. Найдите вероятность того, что меньший из отрезков и 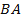имеет длину, меньшую чем .

Ответ: .

2.15. Датчик случайных чисел выдал два числа и в интервале 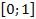. С какой вероятностью корни уравнения действительные? Ответ: .

2.16. На отрезке длины 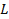произвольно выбраны две точки. С какой вероятностью из трех полученных отрезков можно составить треугольник? Ответ: 1/4.

2.17. На окружности наугад выбирают три точки. Найдите вероятность того, что треугольник с этими вершинами окажется остроугольным. Ответ. .