ОГЛАВЛЕНИЕ
ГЛАВА I ПОЗИЦИОННЫЕ И МЕТРИЧЕСКИЕ ЗАДАЧИ…...........................4
1.1. Образование комплексного чертежа (Эпюр Монжа) …………………...4
1.2. Графическое отображение точки на комплексном чертеже……………4
1.3. Первая основная позиционная задача……………………………………5
1.4. Условия видимости на чертеже…………………………..………………6
1.5. Метрические задачи……………………………………….………………6
1.6. Условия ортогонального проецирования прямого угла………………...6
1.7 Определение натуральной величины отрезка……………………………7
1.8. Алгоритм построения проекции и определения натуральной величины высоты пирамиды и угла наклона (Приложение: Эпюр 1)
………………………………..…..8
ГЛАВА II ПРЕОБРАЗОВАНИЕ ЧЕРТЕЖА……………………...…………..9
2.1. Способ замены плоскостей проекций……………..……………………9
2.2. Алгоритм решения определения натуральной величины высоты пирамиды и основания способом замены плоскостей проекций……..……………10
ГЛАВА III ЛИНИЯ ПЕРЕСЕЧЕНИЯ ДВУХ ПОВЕРХНОСТЕЙ……………11
3.1. Кривые линии и поверхности……………………………………………11
3.2. Линейчатые поверхности и поверхности вращения…………………...11 3.3. Взаимное пересечение кривых поверхностей…………………………. 11
ГЛАВА IV АКСОНОМЕТРИЧЕСКИЕ ЗАДАЧИ……………………………. 13
4.1. Аксонометрические проекции…………………………………………..13
4.2. Алгоритм построения линии пересечения двух поверхностей и
аксонометрической проекции……………………………………………………13
ГЛАВА V РАЗВЕРТКА ПОВЕРХНОСТЕЙ…………………………………. 15
5.1. Развертываемые и не развертываемые поверхности……….. 15
5.2. Алгоритм построения развертки………………………………………...15
ЗАКЛЮЧЕНИЕ………………………………………………………………..16
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ……………………………… 17
ПРИЛОЖЕНИЕ………………………………………………………………. 18
1. Эпюр1…………………………………………………………..18
2. Эпюр 2…………………………………………………………19
3. Эпюр 3…………………………………………………………….20 ВВЕДЕНИЕ.
ГЛАВА I. ПОЗИЦИОННЫЕ И МЕТРИЧЕСКИЕ ЗАДАЧИ.
1.1. Образование комплексного чертежа (Эпюр Монжа).
Эпюр Монжа или комплексный чертеж ‒ это чертеж, составленный из двух или более связанных между собой ортогональных проекций геометрической фигуры.
Одну из плоскостей проекций П1 располагают горизонтально, а вторую П2 - вертикально. П1 ‒ горизонтальная плоскость проекций, П2 ‒ фронтальная. Плоскости бесконечны и непрозрачны (рис. 1а).
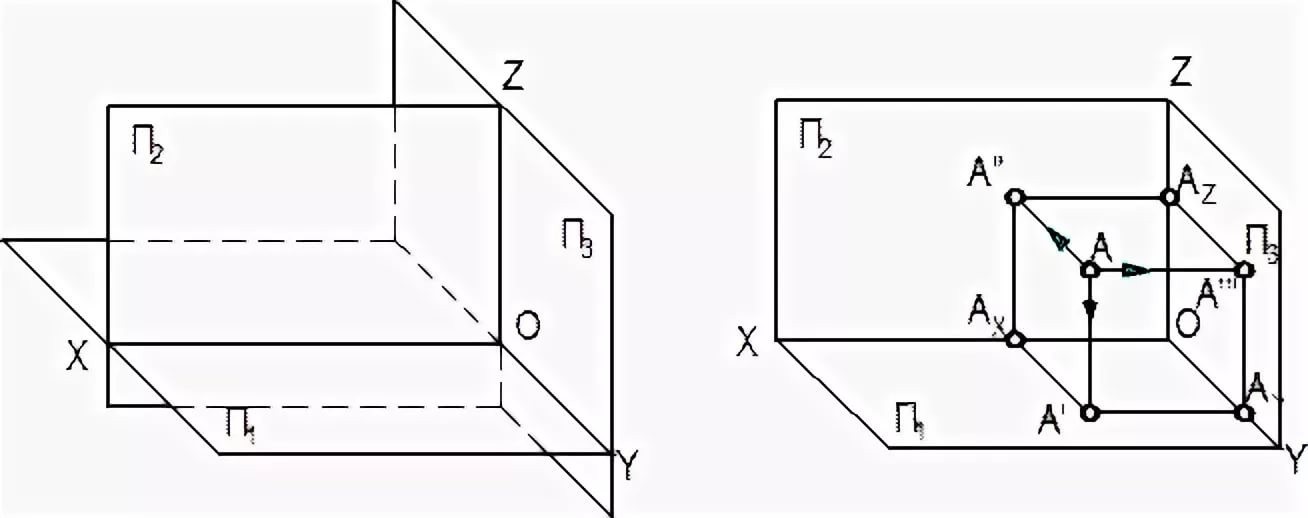
а) б)
Рис 1.
Плоскости проекций делят пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.
1.2. Графическое отображение точки на комплексном чертеже.
Ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. Ортогональные проекции точки А' и А' ' называются соответственно горизонтальной проекцией и фронтальной проекцией (рис. 1б). Проекции точки всегда расположены на прямых, перпендикулярных оси Х12 и пересекающих эту ось в одной и той же точке Аx (так как проецирование прямоугольное). Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи.
1.3 Первая основная позиционная задача.
Позиционными называются задачи на определение каких-либо общихэлементов геометрических объектов, например, точки пересечения прямой и плоскости, линии пересечения двух плоскостей.
Первой основной позиционной задачей называют построение точки пересечения прямой линии с плоскостью общего положения.
На чертеже задана плоскость общего положения Γ(ABC) и прямая общего положения l (рис. 2). Требуется построить точку их пересечения.
Для решения задачи надо выполнить три действия:
1. Через прямую l проведем вспомогательную секущую плоскость Σ и обязательно отметим ее на чертеже. На рисунке вспомогательная плоскость Σ, проходящая через l, выбрана фронтально-проецирующей.
2. Секущая плоскость Σ разрезает данную плоскость ABC. Отмечаем на чертеже линию разреза 1-2.
3. Линия разреза 1-2 и прямая l лежат в одной и той же плоскости (в секущей плоскости Σ). Следовательно, прямые 1-2 и l пересекутся между собой в некоторой точке K. Эта точка и есть искомая точка пересечения прямой l и плоскости ABC. Проверим, правильно ли найдена точка K пересечения прямой l и плоскости Γ(ABC). Эта точка должна одновременно принадлежать и прямой l, и данной плоскости Γ(ABC). Найденная на чертеже точка K – точка пересечения прямой l и линии 1-2. Значит, найденная нами точка K находится и на данной прямой l, и на линии 1-2. Но линия 1-2 находится в плоскости Γ(ABC). Следовательно, точка K находится как на прямой l, так и на плоскости Γ(ABC), то есть K – искомая точка пересечения данной прямой l и данной плоскости Γ(ABC). Точка K найдена правильно.
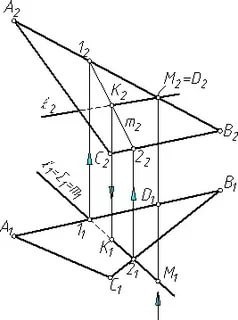
Рис.2.
1.4. Условия видимости на чертеже.
Чтобы сделать чертеж наглядным, удобным для восприятия, прибегают к определению видимости линий на чертеже, Видимость на комплексном чертеже определяется с помощью конкурирующих точек.

Рис.3.
Из двух конкурирующих на виде сверху точек видна та точка, которая выше (рис. 3) – т.А. Из двух точек, конкурирующих на виде спереди, видна та точка, которая ближе (т. е. имеет большую глубину). В нашем случае это точка D.
1.5. Метрические задачи.
Метрическими принято считать задачи, в условии или в решении которых присутствует численная характеристика. К метрическим задачам относятся задачи на построение изображений фигур по их размерам или координатам из точек, измерение расстояний, углов, площадей и другие. Метрические задачи бывают комплексными и включают в своем составе позиционные задачи. Из всего многообразия метрических задач выделяют две задачи, которые называются основными метрическими задачами.
Первая задача - задача на перпендикулярность прямой линии и плоскости.
Вторая основная задача - задача на измерение расстояния между двумя точками способом прямоугольного треугольника.
1.6. Условия ортогонального проецирования прямого угла.
Прямой угол проецируется на горизонтальную, фронтальную и профильную плоскости проекций без искажения, если он образован двумя пересекающимися или скрещивающимися прямыми линиями. Одна из которых является соответственно горизонтальной, фронтальной или профильной линиями уровня, а вторая – составляет с соответствующей плоскостью проекций любой угол, кроме прямого (рис. 4).
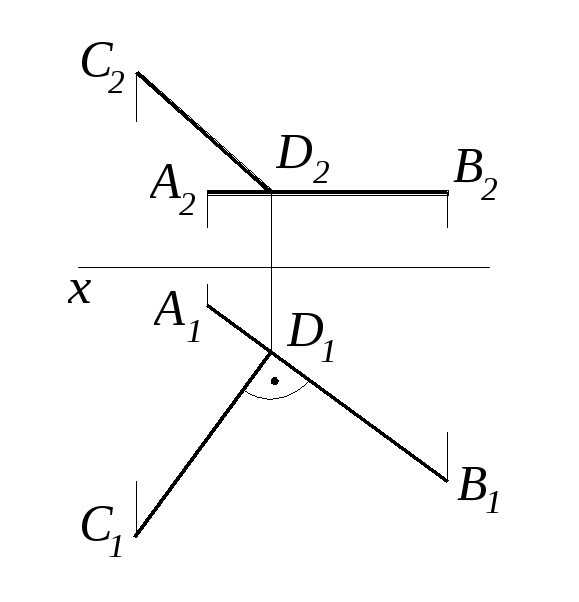
Рис. 4. Проекцирование прямого угла прямого угла
1.7 Определение натуральной величины отрезка.
Натуральная величина отрезка прямой строится как гипотенуза прямоугольного треугольника, одним из катетов которого является проекция отрезка, а другим – разность высот (глубин или широт) концов этого отрезка.
Метод прямоугольного треугольника.
Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.
Для того чтобы найти натуральную величину отрезка AB (рис. 5), строим прямоугольный треугольник A1B1B1'. Его первый катет A'B' – это горизонтальная проекция AB. Второй катет B'B1' равен величине Δ Z =ZA – ZB, то есть разности удаления точек A и B от горизонтальной плоскости П1. Откладываем B'B1' = ZA – ZB перпендикулярно A'B'. Затем проводим гипотенузу A1B1' треугольника A1B'B1'. Её величина соответствует настоящей длине AB.
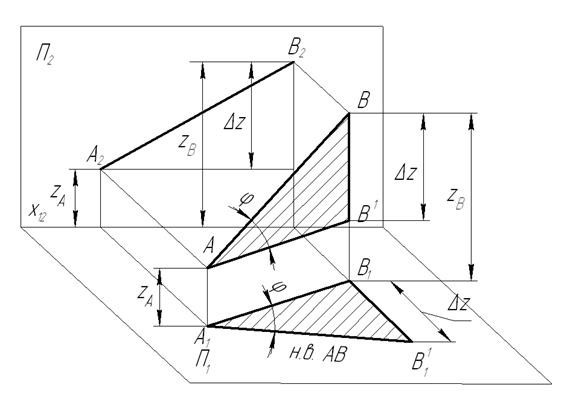
Рис. 5.
1.8. Алгоритм построения проекции и определения натуральной величины высоты пирамиды и угла наклона ребра к основанию (Эпюр 1)
1. Построить точки (высоты пирамиды) по заданным параметрам в Таблице 1 (10 вариант);
2. Через данную прямую l проводим вспомогательную горизонтально проецирующую плоскость Δ (Δ1): Δ ⊃ l и Δ П1;⊥
3. Строим линию пересечения m(m1, m2) этой вспомогательной проецирующей плоскости Δ с данной плоскостью Г (А, В, С); т. е.
m=Δ Г, а также искомую точку пересечения ⋂ D(D1, D2) данной прямой l с построенной прямой m: D=l m ⋂ ∈ Г ⇒ D= l ⋂ Г.
4. С помощью метода прямоугольного треугольника определяем натуральную величину высоты SD. На плоскости П1 соединяем точки А1, D1. Откладываем отрезок А1G, перпендикулярно А1D1. Получаем гипотенузу D1G, которая является натуральной величиной AD.
5. Угол наклона AS к основанию АВС находим из плоскости прямоугольного треугольника ASD. Найдем угол SAD. Определяем натуральную величину SD методом прямоугольного треугольника.
Рассчитываем угол SAD через тангенс.
ГЛАВА II. ПРЕОБРАЗОВАНИЕ ЧЕРТЕЖА. Проекции пространственных объектов, произвольно расположенных относительно плоскостей проекции, не всегда удобны для решения той или иной задачи. Это связано с тем, что имеет место искажение в проекциях натуральных форм и размеров проецируемых объектов. В связи с этим, для более простого решения позиционных и метрических задач проводят преобразование комплексного чертежа таким образом, чтобы получить либо вырожденные проекции элементов объекта, либо их натуральные величины.
2.1. Способ замены плоскостей проекций.
Данный способ состоит в переходе от заданной системы плоскостей проекций к другой системе плоскостей. Положение самого объекта в пространстве при этом остается неизменным.
Пусть точка А(А1, А2) в системе плоскостей проекций П1, П2 (рис. 6). Введем новую плоскость проекций — П4, перпендикулярную П1, и спроецируем на неё точку А. В новой системе плоскостей проекций (П1, П4) получим проекции точки А(А1, А4). При этом останутся неизменными: а) горизонтальная проекция точки A – A1;
б) высота точки А — АА1 =А2А12=А4А14.
Взаимно ортогональные плоскости проекций П1 и П4 абсолютно равноправны. Таким образом, новая система плоскостей проекций представляет собой две взаимно перпендикулярные плоскости, одна из которых взята из старой системыплоскостей проекций, а вторая, перпендикулярная к ней, выбирается так, чтобы проекция объекта на неё давала наилучшее представление о нём.
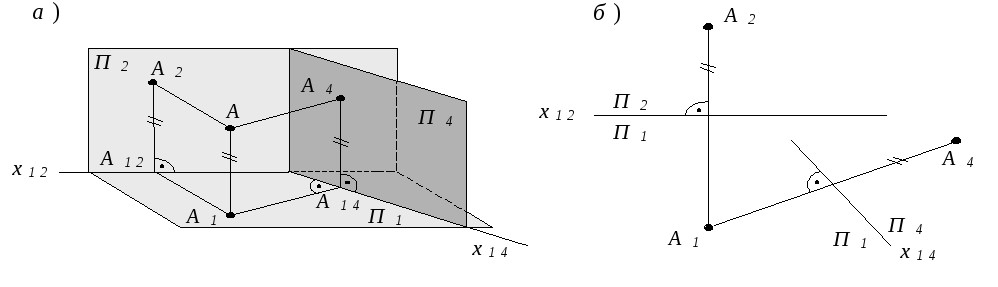
Рис. 6.
Перейдем от системы (П4, П4)к следующей системе (П4, П5), заменив плоскость проекций П1 на П5. При этом:
а) новые линии связи перпендикулярны к новой оси;
б) для получения новой (А5) проекции точки на П5 следует на новой линии связи откладывать расстояние от отбрасываемой оси (Х14) до отбрасываемого изображения (А1).
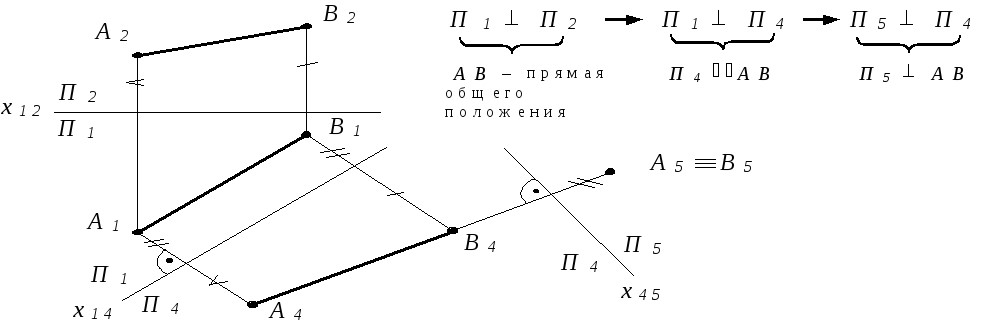
Рис. 7.
2.2. Алгоритм решения определения натуральной величины высоты пирамиды и основания способом замены плоскостей проекций (Эпюр 2).
1. Построить точки (высоты пирамиды) по заданным параметрам в Таблице 1 (10 вариант);
2. Определяем натуральную величину основания пирамиды АВС. Сначала сделаем эту плоскость горизонтально проецируемой. Для этого заменим плоскость П1 новой плоскостью П4, перпендикулярной данной плоскости АВС. Проведем в плоскости АВС фронталь f(f1,f2): на плоскости П1 из т.
С1 проводим проекцию фронтали f1, которая совпадает с ребром В1С1. Следовательно и на П2 f2=В2С2. Проведем новую ось Х24
перпендикулярно f2. Далее на новых линиях связи на расстояние точек А1, В1, С1 строим новые проекции точек А4, В4, С4, которые располагаются на одной прямой — новой проекции плоскости АВС. Теперь от системы (П2, П4) надо перейти к системе (П4, П5), где новая плоскость П5 параллельна плоскости АВС. Для этого проводим новую ось Х45, параллельную А4В4С4, а на линиях связи, проведенных из точек А4, В4, С4 отложим расстояния точек А2, В2, С2. Полочим проекцию А5В5С5 плоскости АВС. Теперь плоскость АВС стала плоскостью уровня и равной натуральной величине треугольника АВС.
3. Определим натуральную величину высоты пирамиды SD. Построим проекцию S4D4 прямой SD. Получим, что проекция S4D4⊥A4B4C4⇒ S4D4 является натуральной величиной SD.
10 ГЛАВА III. ЛИНИЯ ПЕРЕСЕЧЕНИЯ ДВУХ ПОВЕРХНОСТЕЙ.
3.1. Кривые линии и поверхности.
Кривой линией называется след движущийся в пространстве точки. Кривая может быть пространственной или плоской, алгебраической или трансцендентной. Порядком кривой называется число ее точек пересечения с прямой линией или с плоскостью. Кривая линия, составленная из дуг различных кривых, называется обводом.
Поверхность — это непрерывное двухпараметрическое множество точек; это непрерывное однопараметрическое множество линий, имеющее определенный закон образования.
Поверхность на комплексном чертеже задается элементами, однозначно её определяющими. К ним относятся: оси вращения, очерковые линии, центр сферы, меридианы и т. п.
3.2. Линейчатые поверхности и поверхности вращения.
Поверхностью вращения называется такая, которая образуется вращением какой-либо линии, называемой образующей, вокруг прямой, называемой осью вращения.
Окружности, по которым перемещаются точки образующей при её вращении вокруг оси, называются параллелями поверхности вращения.
Кривые линии, получающиеся в сечении поверхности вращения плоскостями, проходящими через ось вращения, называются меридианами. Меридиан, расположенный в плоскости уровня, называется главным.
Поверхность называется линейчатой, если она образуется движением прямой линии (образующей) по заданному закону. Закон движения обычно задается направляющими линиями.
3.3. Взаимное пересечение кривых поверхностей.
Кривые поверхности в общем случае пересекаются по пространственной кривой линии. Проекции кривой строятся при помощи введения вспомогательных секущих поверхностей, выполняющих функции посредников. Секущие плоскости выбираются таким образом, чтобы они пересекались с заданными поверхностями по графически простым линиям: прямым или окружностям. Важно, чтобы эти линии проецирровались на одну из плоскостей проекций без искажения.
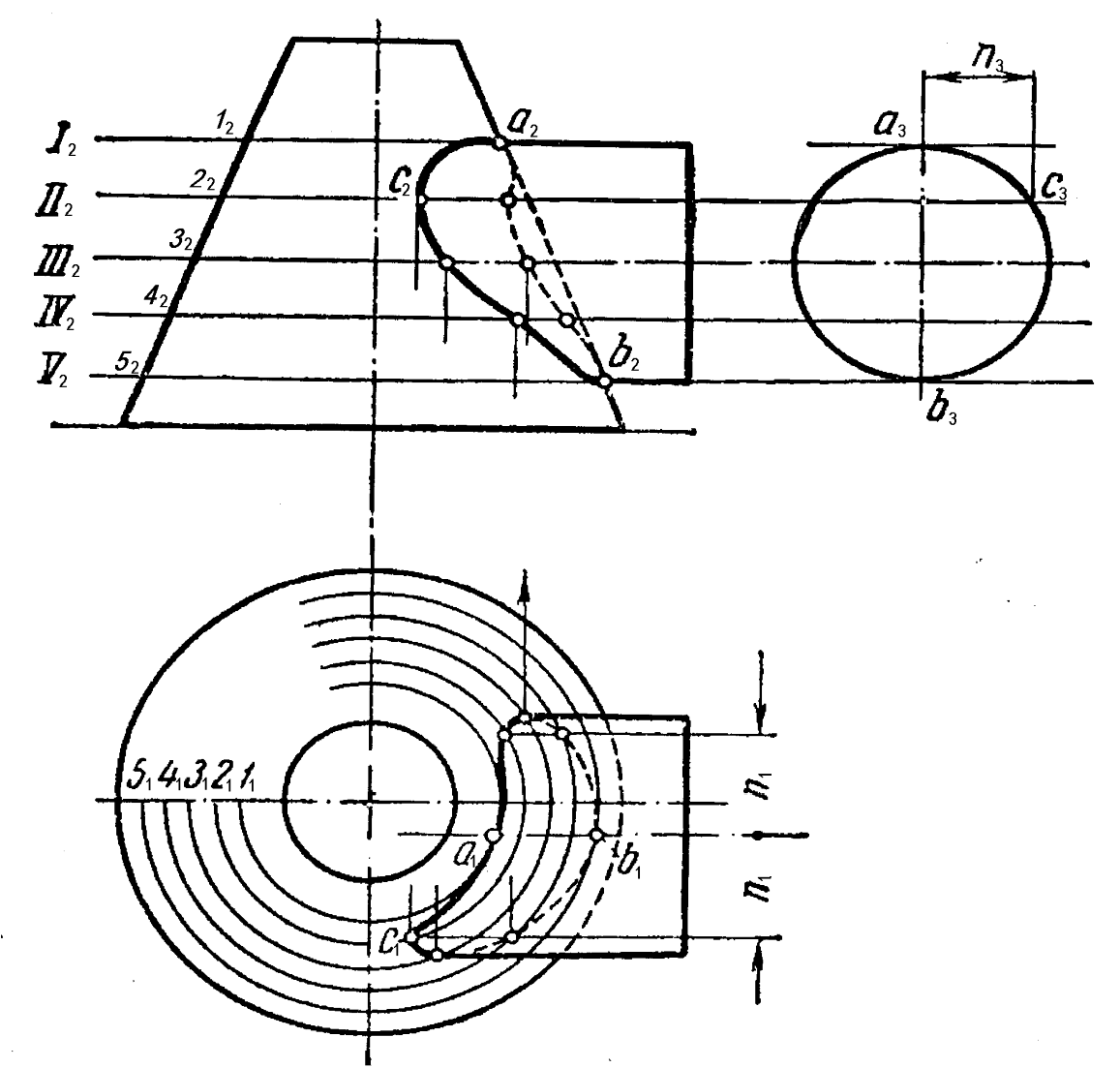 11 Построене линии пересечения поверхностей начинается с построения опорных точек, к которым принадлежат экстремальные точки и точки границ видимости.
11 Построене линии пересечения поверхностей начинается с построения опорных точек, к которым принадлежат экстремальные точки и точки границ видимости.
Экстремальные точки — это точки, принадлежащие граничным поверхностям — посроедникам в пределах области применения последних, а также точки пересеченияч главных меридианов. Точки границ видимости отделяют видимую часть линии пересечения от невидимой и принадлежат очерковым линиям заданных поверхностей.
Рис.8.
Метод вспомогательных плоскостей.
В качестве вспомогательных секущих плоскостей-посредников часто используются плоскости уровня. Для примера рассмотрим линию пересечения поверхностей усеченного конуса и цилиндра вращения(рис. 8). В качестве вспомогательных секущих плоскостей -посредников выбираем горизонтальные плоскости уровня (I, II, III, IV,...), которые рассекают конус по окружностям, а цилиндр — по образующим. Точки их взаимного пересечения и являются точками искомой линии пересечения.
12 ГЛАВА IV. АКСОНОМЕТРИЧЕСКИЕ ЗАДАЧИ.
4.1. Аксонометрические проекции.
Аксонометрия представляет собой один из методов построения наглядных изображений предметов на одной плоскости. Аксонометрические чертеж обладают свойствами наглядности и обратимости -метрической определенности. В зависимости от направления проеецирования на плоскость аксонометрических проекций различают прямоугольную и косоугольную аксонометрию. Отрезки прямых расположенные на осях пространственной системы координат проецируются на аксонометрическую плоскость с искажением. Показатели искажения по осям определяют как отношение длины аксонометрических координатных отрезков к их натуральной величине. Для прямоугольной аксонометрии они равны косинусам углов наклона осей пространственной системы координат к аксонометрической плоскости проекции и обозначаются: u – для оси Х, v- для оси Y, w- для оси Z. В зависимости от соотношений показателей искажения различают: изометрию, диметрию, триметрию.
При изображении окружностей которые проецируются на аксонометрическую плоскость в эллипсы, в прямоугольной аксонометрии руководствуются правилом: большая ось эллипса направлена перпендикулярно отсутствующей в плоскости окружности оси, а малая ось совпадает с её направлением. Большая ось эллипса равна 1,22 d, а малая — 0,71d.
4.2. Алгоритм построения линии пересечения двух поверхностей и аксонометрической проекции (Эпюр 3)(вариант 10)
1. Для решения задачи используем вспомогательные секущие горизонтальные плоскости уровня (Г1, …), которые пересекут поверхности по окружностям, проецирующимеся на плоскость П2 без искажения.
2. Отмечаем опорные точки.
3. Проводим горизонтально проецирующие плоскости уровня Г1, которые пересекают поверхности по окружностям — параллелям. Они спроецируются в натуральную величину на плоскость П2 и, пересекаясь, дадут две точки, принадлежащие искомой линии пересечения. Получим проекции промежуточных точек 1, 2, 3,..., 20 на П2. Проводим линии связи на П1 и отмечаем на соответствующих проекциях плоскостей- посредников Г фронтальные проекции промежуточных точек.
4. Соеденяем проекции точек на П1 и получаем фронтальную проекцию линии пересечения сферы с цилиндром.
5. Построим аксонометрическую проекцию цилиндра в системе координат
ОХ'Y'Z'. Начнем с построения аксонометрической проекцию окружности
13 нижнего основания цилиндра. Такой проекцией является эллипс, имеющий следующее соотношение большой и малой осей: Б.о. = 1,22 d, М.о. = 0,71 d, - где d - диаметр изображаемой окружности. Аналогично строим верхнее основание цилиндра и проводим образующие. Аксонометрическую проекцию линии пересечения строим по координатам точек, принадлежащих ей.
6. Наносим линию пересечения и определяем видимость.
ГЛАВА V. РАЗВЕРТКА ПОВЕРХНОСТЕЙ. Если рассматривать поверхность как гибкую нерастижимую пленку, то, выполнив предварительно разрез по произвольной линии, можно попытаться совместить её с плоскостью без разрывов и складок.
5.1. Развертываемые и не развертываемые поверхности.
Поверхности, обладающие указанными выше свойствами (многогранные, конические, цилиндрические, торсовые), называются равертывающимися, а фигуру, полученную от совмещения поверхности с плоскостью, - разверткой. Все поверхности делятся на развертывающиеся и не развертывающиеся (их иногда называют косыми).
Развертывающиеся поверхности обладают следующими свойствами:
а) длины двух соответственных линий развертки и поверхности равны между собой;
б) углы, образованные линиями на поверхности, и углы между соответственными линиями на развертке также равны;
в) замкнутая линия на поверхности и соответствующая ей линия на развертке ограничивают одинаковые площади, поэтому площадь развертки равна площади соответствующего отсека самой поверхности.
Следствие 1. Прямая на поверхности переходит в прямую на развертке. Следствие 2. Параллельным прямым, лежащим на поверхности, соответствуют параллельные прямые на развертке.
5.2. Алгоритм построения развертки цилиндра (Эпюр 3).
1. Разверткой цилиндра является прямоугольник, высота которого равна образующей, а длина — длине окружности основания, вычисляемой по формуле l= 2π R.
2. Отмечаем образующую FF1, по которой будем производить разрез цилиндра.
3. т. к. длина развертки равна длине окружности, то расстояния точек линии пересечения от образующей FF1 равны длинам соответствующих хорд. Отметим точку В на развертке: на горизонтальной проекции берем расстояние по хорде FB1 и откладываеи на развертке по длине основания цилиндра от точки F, отмечаем точку В'. Из полученной точки проводим образующую цилиндра, на которой откладываем высоту точки В. Аналогично строим все точки линии пересечения.
4. Полученные точки соединяем плавной тонкой линией.
ЗАКЛЮЧЕНИЕ.
Начертательная геометрия является базовым предметом в подготовке студентов инженерных специальностей. При изучении начертательной геометрии студенты приобретают теоретические знания, графические навыки и умения, необходимые для разработки и оформления конструкторской документации. Кроме этого, изучение начертательной геометрии стимулирует развитие пространственного мышления, воображения, инженерной интуиции, изобретательства, то есть тех качеств, которые, несомненно, являются важными в инженерной деятельности.
В процессе изучения данного курса лекций студенты должны научиться по плоским изображениям (проекциям) получать представление о пространственном расположении объектов, научиться строить сечения и развертки различных поверхностей, приобрести графические навыки выполнения чертежей.
Таким образом, изучение студентами данного курса лекций будет способствовать приобретению знаний, умений и навыков, необходимых для успешной сдачи экзамена, зачета или выполнения графических работ.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ.
1. «Начертательная геометрия» Л.Г. Нартова, В.И. Якунин;
2. Рабочая тетрадь по начертательной геометри под редакцией Э.В. Егорова — М., 2018 — 98 с; ил.;
3. Лекции по 1 курсу начертательной геометрии.