Замечания и следствие из теоремы

Основным моментом приведённого доказательства является подстановка , то есть переход к двулистному накрытию плоскости с ветвлением вдоль дискриминантной кривой. Из топологических соображений заранее ясно, что на этом двулистном накрытии двузадачноть исчезает и уравнение распадается на два. Возня с квадратным уравнением нужна лишь для обоснования этого обстоятельства в вещественной области. Полученное на накрытии уравнение (2) остается привести к нормальной форме диффеоморфизмом, опускаемым с накрытия на исходную плоскость – что легко достигается разложением первого интеграла на четную и нечетную по составляющие.

Стоит также отметить, что наше доказательство использовало представление четной функции в виде функции от квадрата аргумента. Для аналитических функций такое представление очевидно. В случае же гладких функций оно нуждается в обосновании.

Действительно, четную бесконечную дифференцируемую функцию модно рассматривать как функцию от квадрата аргумента, заданную на положительной полуоси. Она бесконечно дифференцируема во всех точках этой полуоси, включая нуль. Требуется же представить ее как сужение на положительную полуось функции, бесконечно дифференцируемой на всей оси.

Возможность такого представления означает возможность гладкого продолжения на отрицательную полуось. Она гарантируется теоремой Бореля о существовании бесконечно дифференцируемых функций на прямой с любым лядом Тейлора в нуле. На доказательстве это теоремы мы не останавливаемся.

Кроме регулярных особых точек, в отдельных точках гладкой дискриминантной кривой уравнения общего положения встречаются точки касания контактной плоскости с поверхностью уравнения. В окрестности такой точки уравнение общего положения диффеоморфизм плоскости приводится к нормальной форме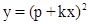

Поле направлений на поверхности уравнения имеет в соответствующей точке криминанты такую же особенность, как поле направлений векторного поля на плоскости в окрестности обыкновенной особой точки типа седло, фокус или узел. Поэтому возникающие здесь особые точки неявных дифференциальных уравнений называются сложенным седлом, фокусом или узлом: они получаются из обычных при помощи отображения складывания. Интересно, что складывание не вносит новых модулей: параметр в нормальной форме определяется отношением собственных чисел линеаризации векторного поля, при складывании фазового портрета которого получается сложенная особая точка.

Примеры решения типовых уравнений

Напоследок хотелось бы разобрать несколько уравнений, не разрешенных относительно производной для наглядности всего вышеперечисленного.

Пример 1

Найти общее решение уравнения .

Это уравнение относится к типу 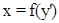(случай 3). Введем параметр и запишем уравнение в виде:

.

Возьмем дифференциалы обеих частей уравнения:

.

Поскольку , то последнее выражение можно представить как

.

Интегрируя, находим зависимость переменной от параметра :

,

где С – произвольная постоянная.

Таким образом, мы получили общее решение уравнения в параметрической форме:

.

Параметр р можно исключить из системы уравнений. Из второго уравнения находим:

.

После подстановки в первое уравнение получаем общее решение в виде явной функции :

.

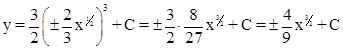Пример 2

Найти общее решение уравнения .

Это уравнение относится к первому случаю, поскольку оно содержит переменную у и ее производную y’. Используя параметр р, мы можем переписать это уравнение в следующем виде:

.

Возьмем дифференциалы от обеих частей:

.

Поскольку , то получаем:

.

Теперь можно проинтегрировать последнее выражение и найти х как функцию р.

.

В итоге мы получаем следующее параметрическое представление решения дифференциального уравнения:

,

где С – произвольная постоянная.

Применение в «жизни»

В настоящее время важную роль в развитии теории дифференциальных уравнений играет применение современных электронных вычислительных машин. Исследование дифференциальных уравнений часто облегчает возможность провести вычислительный эксперимент для выявления тех или иных свойств их решений, которые потом могут быть теоретически обоснованы и послужат фундаментом для дальнейших теоретических исследований.

Итак, первая черта теории дифференциальных уравнений - ее тесная связь с приложениями. Другими словами, можно сказать, что теория дифференциальных уравнений родилась из приложений. Второй особенностью теории дифференциальных уравнений является ее связь с другими разделами математики, такими, как функциональный анализ, алгебра и теория вероятностей.

При изучении конкретных дифференциальных уравнений, возникающих в процессе решения физических задач, часто создавались методы, обладающие большой общностью и применявшиеся без строгого математического обоснования к широкому кругу математических проблем. Такими методами являются, например, метод Фурье, метод Ритца, метод Галёркина, методы теории возмущений и другие. Эффективность применения этих методов явилась одной из причин попыток их строгого математического обоснования. Это приводило к созданию новых математических теорий, новых направлений исследований.

Заключение

Уравнения, не разрешенные относительно производной, до сих пор остается большой загадкой для многих математиков. Большой вклад в исследования этих уравнений внесли такое выдающиеся математики, как Клеро и Лагранж. По сей день их формулировки уравнений используются в биологии, химии, астрофизике и даже в медицине. Но не в таких широких аспектах, как, например, другие типы дифференциальных уравнений. Возможно человечество откроет новые законы природы и в скором времени уравнения, не разрешенные относительно производной будут более востребованы, нежели чем сейчас.

Литература