Графическое оформление и обозначения элементов

Введение

 

Производственная деятельность человека невозможна без применения чертежей. Чертёж — это изображение предмета на плоскости, по которому можно судить о его форме, размерах, устройстве и назначении. Чертёж даёт также и другие необходимые сведения об изображаемом предмете, как-то: материал, особенности изготовления, способы контроля, испытаний и т. п.

Умение быстро и легко воспринимать графическую информацию, т. е. «читать» чертежи, позволяет рабочему добиваться максимальной производительности труда, инженеру – творчески и квалифицированно налаживать производственный процесс. Учитывая, что современное производство все более и более насыщается сложной техникой, обслуживание которой и ее ремонт невозможны без чертежей, становится понятным, как значительна роль чертежа в нашей жизни. Приобретение глубоких знаний в области черчения неразрывно связано с изучением начертательной геометрии, которая является теоретической основой черчения.

Изучение основ начертательной геометрии предполагает самостоятельную проработку учебного материала в соответствии с нижеприведенной программой, а также лекционного курса для студентов-заочников. Для закрепления приобретенных знаний необходимо после прослушивания лекций или самостоятельного изучения курса начертательной геометрии выполнить контрольную работу согласно индивидуальному заданию и выслать в БГСХА (деканат заочного обучения) для последующего рецензирования преподавателями кафедры теоретической механики и инженерной графики.

 

Учебная программа дисциплины

 

1. Введение. Предмет начертательной геометрии (НГ). Основополагающие понятия НГ. Сущность метода проекций. Центральное, параллельное и ортогональное проецирование, их свойства. Комплексный чертеж (КЧ) Монжа. Координатный метод.

2. Проекции точки, линии (прямой) и плоскости на две и три плоско­сти проекций. Следы прямой и плоскости. Позиционные задачи: поло­жение прямой и точки относительно плоскости, принадлежность точки прямой и плоскости, взаимное положение отрезков прямых.

3. Способы задания плоскости на КЧ. Прямая и точка в плоскости. Прямые особого положения. Взаимное положение плоскостей: параллельность, пересечение. Взаимное положение прямой и плоскости: принадлежность, параллельность, пересечение.

4. Метрические задачи: натуральная величина отрезка прямой, углы наклона плоскости и прямой к плоскостям проекций, деление отрезка. Кратчайшее расстояние между точкой и плоскостью, точкой и прямой. Проецирование прямого угла на плоскость проекций. Перпендикуляр к плоскости общего положения. Перпендикулярность двух плоскостей.

5. Способы преобразования КЧ: вращение вокруг проецирующих прямых, вращение вокруг линий уровня. Плоскопараллельное перемещение. Замена плоскостей проекций.

6. Кривые линии, их проекционные свойства. Кривые второго порядка. Касательная и нормаль. Пространственные кривые.

7. Поверхности. Классификация. Определитель поверхности. Кинематический и каркасный способы задания поверхности. Образующая и направляющая. Поверхности вращения, линейчатые, винтовые. Линии на поверхности.

8. Пересечение поверхности плоскостью. Сечения многогранников и поверхностей второго порядка. Истинная величина сечения. Понятие о развертке поверхности. Развертки многогранников, цилиндрической конической и сферической поверхностей. Пересечение прямой с поверхностью.

9. Взаимное пересечение поверхностей. Выбор поверхностей-посредников. Построение линии пересечения поверхностей геометрических тел.

10. Аксонометрическая проекция. Основные понятия. Основная теорема аксонометрии. Коэффициенты искажения и углы проецирования. Стандартные аксонометрические проекции.

 

Требования, предъявляемые к оформлению

Контрольной работы

Общие сведения

Контрольная работа представляет собой несколько чертежей с выполненными графическими решениями конкретных геометрических задач. Графическое решение геометрической задачи представляется двумя (или более) связанными между собой изображениями объектов (точек, линий, фигур и т.п.), т.е. проекциями, построенными на взаимоперпендикулярных плоскостях проекций. В курсе начертательной геометрии чертёж, полученный после совмещения пространственных плоскостей проекций с одной из них, состоящий из нескольких связанных друг с другом проекционных изображений предмета, называется эпюром.

Контрольная работа состоит из пяти задач, которые сведены в три эпюра: эпюр 1 (на позиционные и метрические задачи), эпюр 2 (на пересечение фигуры плоскостью), эпюр 3 (на взаимное пересечение поверхностей). Варианты задач оформляются индивидуальным заданием, выданным и подписанным преподавателем кафедры. На рецензию принимается контрольная работа, которая содержит оригинал индивидуального задания и выполненная в полном объеме.

Контрольная работа представляется на рецензию в сроки, указанные в учебном графике. Эпюры контрольной работы выполняются на листах чертежной бумаги формата А3 (297´420). Поле эпюра ограничивается рамкой, отстоящей от линии обреза листа с левой стороны на 20 мм, с других трёх сторон – 5 мм. В правом нижнем углу формата помещается основная надпись, заполненная по образцу, приведенному в индивидуальном задании.

 

Графическое оформление и обозначения элементов

Все задачи выполняются с помощью чертежных инструментов в заданном или выбранном масштабе (ГОСТ 2.302–68) с учетом наиболее равномерного распределения изображений в пределах формата листа.

Линии на чертежах должны соответствовать ГОСТ 2.303–68.Все основные вспомогательные построения должны быть сохранены. Надписи, как и отдельные обозначения, в виде букв и цифр, должны быть выполнены шрифтом чертежным в соответствии с ГОСТ 2.304–81.

Обозначение точек, прямых, плоскостей, углов при решении задач контрольной работы является обязательным. Принятая система обозначений объектов (элементов) и взаимосвязей между ними приведена в табл. 2.1 и 2.2.

Следует уделить серьезное внимание тщательности и аккуратности всех графических работ. Небрежно выполненные построения не только снижают качество чертежа, но и приводят к неправильным результатам. В случае небрежного или неправильного оформления контрольных работ студенту может быть предложено дополнительное задание, например, выполнить буквы и цифры шрифта и т.п.

Титульный лист, комплект чертежей контрольной работы и индивидуальное задание должны быть сложены друг с другом и сброшюрованы тесьмой или лентой в альбом формата А4.

Складывание чертежей выполняется в соответствии с ГОСТ 2.501–88. Листы формата А3 складывают "гармошкой" до формата А4 (рис. 2.1,б) изображением наружу так, чтобы основная надпись оказалась на верхней лицевой стороне в нижнем правом углу. Листы следует сгибать по линиям, перпендикулярным основной надписи, в порядке, указанном цифрами 1, 2 (рис.2.1,а) на линиях сгибов.

 

 

Рис.2.1.Схема складывания формата А3 по линиям сгиба.

 

Т а б л и ц а 2.1. Обозначения геометрических объектов

 

Объект	Обозначение	Пример	Расшифровка
Точка	Прописная буква латинского алфавита или цифра	А, В, С, 1 …	Точка A, точка B, точка C, точка 1
Произвольная линия: прямая, кривая; задана точками; отрезок; дуга	Строчная буква латинского алфавита Прописные буквы	a, b, c…   AB, CD, … AB, ABC	Прямая a, ломаная b, кривая c Прямая AB, линия CD Отрезок AB, дуга ABC
Поверхность:   В т.ч.: плоскость при задании плоскости точками при задании плоскости прямыми	Прописные буквы греческого алфавита Строчные буквы греческого алфавита Прописные буквы латинского алфавита Строчные буквы	Σ,Ω…   α, β, γ,..   A,B,C, …   α (a ∩ b), …	Поверхность Σ, поверхность Ω Плоскость α, β, γ   Плоскость АВС   Плоскость α заданная пересекающимися прямыми a и b
Плоскость и поле проекций	Прописная буква «пи» греческого алфавита	П, П1, П2, П3, …	Плоскость (поле) проекций П, П1–плоскость «пи» 1 и т. д.
Фигура или геометрическое тело	Прописная буква «фи» греческого алфавита	Ф1, Ф2,…	Фигура Ф1, геометрическое тело Ф2 и т. д.
Угол линейный	Знак угла и буква α, β,	α, β	Угол α, угол β

 

Примечание. Проекция объекта обозначается той же самой буквой, но с индексом плоскости проекций. Например: A₁ – проекция точки A на горизонтальную плоскость проекций; b₂ – проекция прямой на фронтальную плоскость проекций; α₃ – профильный след плоскости α, П₁ – горизонтальная плоскость проекций и т.д.

 

Т а б л и ц а 2.2. Знаки взаиморасположения геометрических объектов

 

Знак	Смысл знака	Пример	Расшифровка знака
∩   Є   ||   ^   Ō   =   ≡   /	Пересечение   Принадлежность   Параллельность   Перпендикулярность   Касание   Результат или равенство     Совпадение   Отрицание (не)	a ∩ b   A Є a   a || α   α ^ β   a Ō b   a ∩ b = С   AB = CD   A ≡ B   AB ≠ CD	Прямая a, пересекающаяся с прямой b Точка A принадлежит прямой a   Прямая а параллельна плоскости α Плоскость α перпендикулярна плоскости β Прямая a касается кривой b   Точка C – результат пересечения прямых a и b Отрезок AB равен отрезку CD   Точка A совпадает с точкой B   Отрезки AB и CD не равны

 

Первая страница (титульный лист) контрольной работы должна быть оформлена по приведенному образцу (рис. 2.2). Надписи следует выполнять чертежным шрифтом типа А или Б размером 5;7;10.

Допускается выполнять титульный лист и эпюры с использованием персональных компьютеров и плоттеров.

Контрольные работы, оформленные с отступлением от изложенных выше требований, не рецензируются и отсылаются студенту для переоформления.

 

 

 

Рис.2.2. Образец выполнения титульного листа.

 

 

Выполнение задач эпюров

Эпюр № 1

 

Эпюр 1 разделен на две задачи, соответствующие разделам 2, 3, 4 учебной программы.

Заданы координаты точек A, B, C, D, E. Выполнить графические построения для решения нижеследующих задач.

Задача 1. Задать плоскость, проходящую через точку D параллельно треугольнику ABC, и определить кратчайшее расстояние между двумя плоскостями.

Задача 2. Перпендикулярно треугольнику ABC, через отрезок DE провести плоскость. Построить линию пересечения взаимоперпендикулярных плоскостей и определить видимость линий, задающих эти плоскости.

Данные для выполнения эпюра взять из индивидуального задания. Координаты точек даны в миллиметрах. Точка Е используется только для решения 2-й задачи.

Пример выполнения эпюра № 1 представлен на рис. 3.1. При решении задач нужно исходить из следующих основных положений.

1. В основе построения любого изображения имеет место операция проецирования, т.е. своеобразный перенос объекта из трехмерного пространства на двумерную поверхность. Наиболее элементарный геометрический объект, которым является точка, также имеет соответствующее отображение (проекцию) на плоскости проекций.

2. Ортогональная проекция точки на плоскость есть точка, находящаяся в основании перпендикуляра, опущенного из рассматриваемой точки на выбранную плоскость.

3. Положение точки в выбранной либо заданной системе плоскостей проекций однозначно определяется любыми двумя проекциями этой точки, так как по ним можно установить расстояние от точки до каждой из трех плоскостей проекций, т. е. определить три координаты данной точки.

4. Проекции точки в ортогональной системе плоскостей проекций попарно располагаются на линиях, перпендикулярных к соответствующим осям проекций. Эти линии называются линиями проекционной связи.

5. Прямые линии, параллельные плоскостям проекций, проецируются на эти плоскости без искажения. Это линии уровня: горизонталь, фронталь, профильная прямая. На рис. 3.2 АВ||П₁, горизонтальная проекция А₁В₁ равна длине самого отрезка и А₂В₂||ОХ. Прямая СD||П₂, фронтальная проекция С₂D₂ = СD и С₁D₁||ОХ.

 

 

 

 

Рис. 3.2.

 

если две проекции прямой параллельны одной и той же оси проекций (OX или OY или OZ), то такая прямая занимает проецирующее положение (перпендикулярна плоскости проекций). Проецирующая прямая проецируется в точку на плоскость проекций, к которой она перпендикулярна, а на две другие плоскости проекций – в натуральную величину.

На рис. 3.3,а горизонтально проецирующая прямая АВ проецируется на П₁ в точку (А₁ºВ₁), a А₂В₂=АВ и А₃В₃=АВ. На рис. 3.3,б задан отрезок фронтально проецирующей прямой. Здесь фронтальная проекция C₂D₂ представляет собой точку, а две другие проекции отрезка C₁D₁ и C₃D₃ равны длине отрезка CD.

 

Рис. 3.3.

 

6. Следует иметь в виду, что прямая линия, расположенная под некоторым острым либо тупым углом к плоскости проекций, проецируется на неё с искажением. Длина отрезка прямой линии общего положения и угол наклона этой прямой к плоскости проекций могут быть определе­ны при построении соответствующего прямоугольного треугольника. Если определяется угол наклона прямой к П₁, то одним катетом треугольника является горизонтальная проекция отрезка прямой A₁B₁, а вторым – разность аппликат точек A и B – ΔZ (рис. 3.4,а,б). Гипотенуза треугольника равна длине отрезка. Если определяется угол наклона прямой к П₂, то один катет равен фронтальной проекции отрезка, а второй – Δу (разность ординат). Гипотенуза же построенного треугольника снова идентична действительной величине отрезка.

 

Рис. 3.4.

 

7. При определении взаимного расположения двух прямых линий следует помнить признаки параллельности и пересечения прямых:

а) если прямые линии в пространстве параллельны, то их одноименные проекции (k₁ и l₁, k₂ и l₂) параллельны (рис. 3.5,а);

б) если прямые линии в пространстве пересекаются, то одноименные проекции их также пересекаются (рис. 3.5,б) и точки (1₁ ,1₂) пересечения этих проекций лежат на линии проекционной связи;

в) если прямые линии не параллельны и не пересекаются, то они являются скрещивающимися. Точки пересечения одноименных проекций этих линий определяют конкурирующие точки. На рис. 3.5,в точки 1, 2 – горизонтально конкурирующие, из них точка 1 – видимая, точки 3, 4 – фронтально конкурирующие, из них точка 3 – видимая.

 

Рис. 3.5.

8. Если две пересекающиеся прямые линии взаимно перпендикулярны и занимают в системе плоскостей проекций общее положение, то угол между проекциями этих линий – произвольный (острый или тупой). Если же одна из них параллельна плоскости проекций, то проекции прямых на этой плоскости проекций также взаимно перпендикулярны. На рис. 3.6, а, б AB^BC, ВС||П₁, A₁B₁^B₁C₁. На рис. 3.6,в DE^EF, DЕ||П₂, D₂E₂^E₂F₂.

 

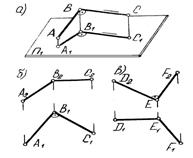
рис. 3.6.

 

9. Объектом проецирования и отображения на комплексном чертеже может быть плоскость. Она в системе плоскостей проекций может занимать как общее (т. е. наклонное под произвольным углом к плоскостям проекций), так и частное (параллельно либо перпендикулярно плоскости проекций).

Наиболее характерно отображается плоскость, если она задана плоской фигурой (многоугольником, сектором, кругом и т. п.). Если рассматриваемая плоскость занимает частное положение, то одна из её проекций вырождается в отрезок прямой, который одновременно является следом данной плоскости. Если же аналогичная плоскость задаётся своими следами, то один из следов плоскости располагается перпендикулярно к одной из присутствующих осей проекций. По этим признакам и следует отличать на комплексном чертеже плоскости общего (непараллельные и неперпендикулярные плоскости проекций) и частного положения (параллельные или перпендикулярные плоскости проекций). Плоскости, располагающиеся параллельно одной из трёх плоскостей проекций, – это плоскости уровня: горизонтальные (||П₁) (рис. 3.9, а, б) и фронтальные (||П₂) (рис. 3.10, а, б). Плоскости, перпендикулярные одной плоскости проекций, а к двум другим наклонные, – проецирующие плоскости: горизонтально проецирующие (^П₁) (рис. 3.7, а, б) и фронтально проецирующие (^П₂) (рис. 3.8, а, б). Вышеперечисленные плоскости применяются при решении многих задач как вспомогательные (плоскости-посредники).

Рис. 3.7.

 

Рис. 3.8.

 

При этом используется свойство проецирующей плоскости, которое заключается в том, что все точки и фигуры горизонтально проецирующей плоскости проецируются в одну линию на П₁, фронтально проецирующей плоскости – в одну линию на П₂. Фигуры, расположенные в горизонтальной плоскости уровня, проецируются на П₁ в натуральную величину, а на П₂ и П₃ – в прямые линии, а фигуры, расположенные во фронтальной плоскости уровня, на плоскость П₂ проецируются в натуральную величину, а на П₁ и П₃ – в прямые линии.

Рис. 3.9.

 

10. В процессе решения многих задач используются главные линии плоскости, такие как горизонталь и фронталь.

Рис. 3.10.

 

Горизонталь h – это линия, принадлежащая данной плоскости и параллельная плоскости П₁ (рис. 3.11,а,б,в). Фронталь f – это линия, лежащая в плоскости и параллельная П₂ (рис. 3.11).Иногда используется линия наибольшего ската т.е. линия, лежащая в плоскости и перпендикулярная к горизонталям плоскости.

 

 

Рис. 3.11.

 

11. При решении задач на пересечение плоскостей необходимо учитывать следующее:

а) горизонтальная плоскость уровня пересекает все другие плоскости по горизонталям. Нарис. 3.12,а горизонтальная плоскость s пересекает плоскость треугольника ABC по горизонтали h(h₁; h₂);

б) фронтальная плоскость уровня пересекает все другие плоскости по фронталям. На рис. 3.12,б фронтальная плоскость g пересекает плоскость четырехугольника ABCD по фронтали f(f₁; f₂);

в) если одна из взаимно пересекающихся плоскостей проецирующая, то одна проекция линии пересечения известна. Она совпадает со следом этой плоскости, вторая же и третья проекции определяются условием принадлежности прямой линии (отрезка) плоскости и строятся по линиям проекционной связи.

Рис. 3.12.

 

На рис. 3.13 горизонтально проецирующая плоскость a пересекает плоскость общего положения g (h∩f). Горизонтальная проекция линии пересечения 1₁2₁ находится на следе a₁, фронтальная проекция 1₂2₂ определяется по линиям проекционной связи.

 

Рис. 3.13.

 

12. Из множества вариантов взаимного положения прямой линии и плоскости наиболее часто встречается задача на пересечение прямой и плоскости. При решении задач на пересечение прямой линии и плоскости следует отличать общие и частные случаи.

Если прямая общего положения пересекает плоскость частного положения, то одна проекция точки пересечения находится без дополнительных построений. Она определяется, как правило, пересечением проекции прямой линии и следа вышеупомянутой плоскости на той плоскости проекций, к которой данная плоскость перпендикулярна. Вторая и третья проекции искомой точки строятся по правилу принадлежности точки прямой линии, используя линии связи.

 

Если пересекающиеся между собой объекты, т.е. прямая линия и плоскость, занимают общее положение, то задача решается по следующему алгоритму:

а) через прямую линию проводится вспомогательная плоскость-посредник;

б) строится линия пересечения заданной плоскости и плоскости-посредника;

в) в пересечении построенной линии и заданной прямой отмечается искомая точка пересечения прямой с плоскостью.

При помощи плоскости-посредника получена точка пересечения (K₁, K₂) прямой l с плоскостью треугольника ABC (рис. 3.14). Для этого вводится aÎ l, a^П₁, a∩s (ΔАВС) = 12, 12∩ l = К.

 

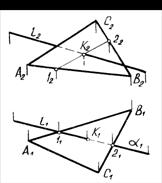
рис. 3.14.

 

13. При пересечении прямой линии с плоскостью особый интерес представляет вариант перпендикулярности линии и плоскости. Линия перпендикулярна плоскости, если она располагается под прямым углом к двум пересекающимся и лежащим в этой плоскости прямым. Наиболее очевидным является тот случай, когда в качестве этих пересекающихся прямых выступают фронталь и горизонталь (прямые углы между данной линией и линиями уровня проецируются в натуральную величину на соответствующие плоскости проекций).

Проверяя перпендикулярность прямой линии и плоскости по проекциям этих объектов, всегда рассматриваем положение проекций данной линии и линий уровня плоскости. Прямая линия перпендикулярна плоскости, если горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали данной плоскости, а фронтальная проекция рассматриваемой прямой перпендикулярна фронтальной проекции фронтали этой же плоскости. На рис. 3.15 DK^h и DK^f, DK^s (ΔАВС).

 

рис. 3.15.

 

Если плоскость, с которой пересекается прямая линия, перпендикулярна плоскости проекций, т. е. занимает проецирующее положение, то при определении точки пересечения, вспомогательная плоскость-посредник не вводится. На рис. 3.16,агоризонтально проецирующая плоскость aпересекает прямую l вточке К, а на рис. 3.16,бфронтально проецирующая плоскость треугольника ABC пересекает прямую l в точке К.

 

рис. 3.16.

 

14. При решении задач на параллельность прямой линии и плоскости следует исходить из того, что прямая параллельна плоскости, если она параллельна какой-то прямой, лежащей в плоскости, или если через имеющуюся прямую можно провести плоскость, параллельную заданной. Прямая n (рис. 3.17) параллельна плоскости g(ΔАВС), так как она параллельна прямой В1, принадлежащей плоскости.

 

рис. 3.17.

 

На рис. 3.18,а прямая линия l параллельна горизонтально проецирующей плоскости a, а на рис. 3.18,б прямая m параллельна фронтально проецирующей плоскости b.

15. Признак перпендикулярности двух плоскостей формулируется следующим образом: если первая плоскость проходит через прямую, расположенную под прямым углом к другой плоскости, то обе плоскости перпендикулярны друг другу. На рис. 3.19 MK^s(ΔАВС) и g(МК∩MN)^s(ΔАВС).

 

 

Рис. 3.18.

Рис. 3.19.

 

16. если плоскости параллельны, то две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. На рис. 3.20 через точку А проведена плоскость a(l ||m), параллельная плоскости ΔАВС.

 

Рис. 3.20.