Этапы решения 1-й задачи на комплексном чертеже.

1. По заданным координатам построить треугольник АВС и точку D.

2. через точку D провести плоскость, образуя её двумя пересекающимися прямыми, параллельными соответствующим сторонам треугольника AВС.

3. определить расстояние между плоскостями, для этого:

а) или из точки Dопустить перпендикуляр на плоскость треугольника ABC и найти точку пересечения перпендикуляра с плоскостью треугольника. После этого определить натуральную величину построенного перпендикуляра;

б) либо из точки A(B,C) опустить перпендикуляр на плоскость, проведенную через точку D, затем найти точку его пересечения с плоскостью и определить натуральную величину этого перпендикулярного отрезка.

Этапы решения 2-й задачи на комплексном чертеже.

1. по координатам построить треугольник АВС и прямую DЕ.

2. Через точку D провести прямую, перпендикулярную плоскости треугольника АВС, в результате чего образуется участок плоскости, перпендикулярной плоскости треугольника.

3. для определения линии пересечения двух плоскостей построить точки пересечения перпендикуляра и прямой DЕ с плоскостью треуголь­ника ABC, затем одноименные проекции построенных точек соединить.

4. определить видимость заданной и построенной плоскостей.

Эпюр № 2

Дано элементарное геометрическое тело (одно или два) и плоскость, пересекающая поверхности этого тела. Геометрическое тело задаётся, как правило, фронтальной и горизонтальной проекциями. Секущая плоскость задаётся следами этой же плоскости и занимает частное положение: является проецирующей плоскостью или плоскостью уровня. Плоскость может задаваться двумя пересекающимися прямыми и занимать общее положение. В этом случае поверхность заданного тела занимает частное (проецирующее) положение.

Требуется: 1) построить третью проекцию заданного геометрического тела и определить три проекции линии пересечения заданной поверхности плоскостью; 2) получить натуральную величину сечения геометрического тела плоскостью; 3) построить развёртку поверхности тела и показать на развертке линию пересечения поверхности плоскостью; 4) построить аксонометрические проекции геометрических тел с линией пересечения их поверхностей.

Задание выполняется на формате A3 и предполагает последовательное решение четырёх задач в соответствии с вышеуказанными пунктами 1–4. При необходимости, развёртка и аксонометрия геометрического тела может быть построена на отдельном формате А3 или А4. Данные для исходного варианта эпюра взять из индивидуального задания. Примеры выполнения приведены на рис. 3.21. При построении линий контура сечения считать поверхности и секущие плоскости непрозрачными. На всех чертежах линию пересечения поверхности с плоскостью следует выделить, например, цветным карандашом.

Прежде чем приступить к выполнению эпюра № 2, необходимо повторить по рекомендованной литературе разделы: плоскость и задание точек и прямых линий на плоскости; пересечение плоскостей; пересечение прямой линии и плоскости; поверхности и задание точек и линий на поверхности. Проработать способы преобразования проекций: вращение вокруг осей, перпендикулярных и параллельных плоскостям проекций, замену плоскостей проекций.

Решение 1-й задачи. Третья, т. е. профильная проекция тела выполняется по известным координатам точек тела, взятым с горизонтальной и фронтальной проекций фигуры. Для профильной проекции учитываются ординаты (Y) и аппликаты (Z) точек. Все три проекции рассматриваемой точки должны находиться в строгой проекционной связи.

При пересечении многогранника плоскостью следует исходить из того, что сечением многогранника является многоугольник, проекции которого определяются несколькими точками или отрезками. В первом случае задача сводится к определению точки пересечения прямой линии (ребра) с плоскостью, а во втором – к построению линии пересечения двух плоскостей – грани и секущей плоскости.

 

 

Необходимо усвоить, что если секущая плоскость – проецирующая, то одна из проекций сечения вырождается в прямую линию, совпадающую со следом плоскости. Вторая и третья проекции строятся по условию принадлежности точек сечения и поверхности тела и секущей плоскости, используя линии проекционной связи. На рис. 3.22 фронтально проецирующая плоскость β пересекает пирамиду по треугольнику 1-2-3. Фронтальная проекция сечения 1₂2₂3₂ определяется точками пересечения проекций ребер пирамиды со следом плоскости β₂.

 

рис. 3.22.

 

Горизонтальные проекции вершин треугольника сечения 1₁2₁3₁ определяются на соответствующих ребрах пирамиды по линиям проекционной связи. На рис. 3.23 призма пересекается горизонтально проецирующей плоскостью α. В этом случае известна горизонтальная проекция сечения 1₁2₁3₁4₁, совпадающая со следом α₁, а фронтальная проекция 1₂2₂3₂4₂ определяется по линиям проекционной связи.

Следует обратить внимание на то, что если секущая плоскость занимает общее положение, но грани поверхности представляют собой проецирующие плоскости, то одна из проекций сечения также известна. Так, на рис. 3.24 призма, грани которой перпендикулярны плоскости проекций П₁, пересекается плоскостью α, заданной двумя пересекающимися прямыми h и f. Фигурой сечения является пятиугольник 1-2-3-4-5. Верхнее основание призмы A¹B¹C¹D¹ представляет собой горизонтальную плоскость уровня и пересекается с плоскостью α(h∩f) по горизонтали h¹(h¹₁; h¹₂), на которой находятся проекции стороны сечения 1₁2₁ и 1₂2₂. Грань призмы АА¹ВВ¹ является фронтальной плоскостью уровня, пересекает плоскость (h∩f) по фронтали f¹(f¹₁; f¹₂), на которой расположена сторона сечения 4-5(4₁5₁; 4₂5₂).Грань АА¹DD¹ является горизонтально проецирующей плоскостью, пересекает плоскость (h∩f) no линии 6-7(6₁7₁; 6₂7₂), на которой расположена сторона сечения 3-4(3₁4₁; 3₂4₂).

 

Рис. 3.23.

 

 

Рис. 3.24.

 

Прежде чем приступить к решению задач на пересечение кривых поверхностей плоскостью, следует изучить и четко представить, что плоскость может пересекать прямой круговой цилиндр по окружности, образующим и эллипсу; конус – по окружности, образующим, эллипсу, параболе или гиперболе, сферу – по окружности.

В общем случае кривая поверхность пересекается плоскостью по кривой линии, которая определяется рядом точек. Для линейчатых поверхностей эти точки могут быть точками пересечения образующих с секущей плоскостью. Обычно вначале находятся особые точки: точки «видимости», «высшие» и «низшие» и другие, а затем все остальные точки. Через эти точки проводится плавная кривая линия. Чем больше получено таких точек, тем точнее определяется искомая линия пересечения.

В тех задачах, где кривая поверхность пересекается проецирующей плоскостью, одна из проекций сечения совпадает со следом плоскости, а вторая проекция определяется посредством проведения на кривой поверхности простейших линий – прямых или окружностей. На рис. 3.25фронтально проецирующая плоскость β пересекает конус по эллипсу, фронтальная проекция которого вырождается в прямую линию и совпадает со следом плоскости β₂.

 

Рис. 3.25.

 

Горизонтальная проекция определяется особыми точками 1, 2, 3, 4 и общими 5, 6 и др. Низшая 1(1₁; 1₂) и высшая точки 2(2₁; 2₂) расположены на очерковых образующих l (l ₁; l ₂)и l ¹(l ₁¹; l ₂¹). Горизонтальные проекции точек 3 и 4, определяющих малую ось эллипса, находятся посредством окружности m(m₁; m₂), расположенной на поверхности конуса. Точки 5 и 6 найдены при помощи образующих l ² и l ³. Таким же способом строятся достаточное количество точек, определяющих горизонтальную проекцию сечения. На рис. 3.26 круговой наклонный цилиндр пересекается горизонтально проецирующей плоскостью α. Горизонтальная проекция сечения совпадает со следом плоскости α₁, фронтальная проекция определяется по ряду точек. Высшая точка сечения 1 (1₁; 1₂) находится на верхнем основании цилиндра, а низшая 2(2₁; 2₂) – на образующей l (l ₁; l ₂).Точки видимости 3(3₁; З₂) и 4(4₁; 4₂) расположены на образующих l ¹(l ₁¹; l ₂¹) и l ²(l ₁²; l ₂²). Крайние точки слева и справа 5(5₁; 5₂) и 6(6₁; 6₂) находятся на образующих l ³(l ₁³; l ₂³) и l ⁴(l ₁⁴; l ₂⁴).

 

Рис. 3.26.

 

На рис. 3.27 горизонтально проецирующая плоскость α пересекает сферу. Горизонтальная проекция сечения совпадает со следом плоскости α₁, а фронтальная проекция представляет собой эллипс, который определяется особыми и общими точками.

Вначале отмечаются горизонтальные проекции этих точек, затем с помощью окружностей сферы находятся ихфронтальные проекции. Например, низшая и высшая точки 1(1₁; 1₂) и 2(2₁; 2₂), определяющие большуюось эллипса, получены с помощью окружностей l ¹(l ₁¹; l ₂¹), l ²(l ₁²; l ₂²),точки 3(3₁; З₂) и 4(4₁; 4₂), определяющие малую ось эллипса, расположены на окружности l ³(l ₁³; l ₂³), точки видимости 5(5₁; 5₂) и 6(6₁; 6₂) лежат на окружности l ⁴(l ₁⁴; l ₂⁴), общие точки 7(7₁; 7₂) и 8(8₁; 8₂) определены посредством окружности l ⁵(l ₁⁵; l ₂⁵).

 

 

Рис. 3.27.

 

Следует обратить внимание на особенность решения тех задач, в которых поверхность является проецирующей, а секущая плоскость –общего положения. В таких задачах одна из проекции фигуры сечения также известна. Она совпадает с проекцией поверхности, а вторая проекция определяется с помощью линий, проведенных на секущей плоскости.

На рис. 3.28 плоскость общего положения (h∩f) пересекает прямой круговой горизонтально проецирующий цилиндр. Линией пересечения цилиндра плоскостью является эллипс, горизонтальная проекция которого совпадает с проекцией цилиндра – окружностью, а фронтальная проекция определяется по точкам 1, 2, 3 и др. Высшая 1(1₁; 1₂) и низшая точки 2(2₁; 2₂) определяются с помощью линии наибольшего ската

MN (M₁N₁, M₂N₂), пересекающей осьцилиндра. Низшая точка 2 находится за пределами цилиндра, поэтому определяется линия пересечения нижнего основания цилиндра с секущей плоскостью (h∩f). Основание цилиндра представляет собой горизонтальную плоскость уровня, пересекающуюся с плоскостью (h∩f) по горизонтали h¹(h₁¹; h₂¹), на которой расположены искомые точки 3(3₁; З₂) и 4(4₁; 4₂). По известным горизонтальным проекциям 5₁ и 6₁точек видимости с помощью фронтали f¹(f¹₁; f¹₂) плоскости (h∩f) определяются фронтальные проекции точек 5₂ и 6₂. На рис. 3.29 цилиндр пересекается плоскостью общего положения, заданной четырехугольником ABCD. Горизонтальная проекция сечения совпадает с проекцией цилиндра – окружностью, на которой отмечаются точки 1₁; 2₁; 3₁,..., а затем определяются их фронтальные проекции 1₂; 2₂; 3₂,..., используя при этом линии секущей плоскости четырехугольника ABCD. Так, низшая точка 1 распо-

 

Рис. 3.28.

 

ложена на линии наибольшего ската, точки 2, 3, – на горизонтали h, точки видимости 4 и 5 – на горизонталях h¹ и h², точки 6 и 7, определяющие малую ось эллипса, – на горизонтали h³.

 

рис.3.29.

Решение 2-ой задачи. Натуральная величина сечения заданного геометрического тела плоскостью отображается в том случае, когда плоскость сечения параллельна плоскости проекций. Во всех иных вариантах фигура сечения проецируется на плоскость проекций с искажением. Расположить фигуру сечения параллельно плоскости проекций можно одним из способов преобразования эпюра – вращением или заменой плоскостей проекций. Если эту фигуру предполагают разместить параллельно плоскости П₁, то самое рациональное решение дает вращение фигуры вокруг одной из горизонталей этого сечения. На рис. 3.30 действительная величина сечения A₀B₀С₀ ΔABC построена вращением фигуры вокруг горизонтали h. Точка А неподвижна, так

Рис. 3.30.

 

как находится на оси вращения h, а точка С вращается в горизонтально проецирующей плоскости вокруг центра О. Радиусом вращения является отрезок ОС, длина которого О₁С₁¹ получена по способу прямоугольного треугольника и отложена на следе α₁ от точки O₁. Третья вершина В₀ получена в пересечении следа α₁¹ плоскости вращения и стороны треугольника, проходящей через полученную точку С₀ и неподвижную точку 1₁,(α₁¹∩C₀1₁=B₀).

Если плоскость фигуры сечения занимает горизонтально проецирующее положение, то определение натуральной величины сечения вращением вокруг горизонтали значительно упрощается. Не требуется определять длину радиусов вращения, так как в этом случае они являются горизонтально проецирующими прямыми и проецируются на П₂ без искажения. Поэтому для определения натуральной величины A₀B₀C₀ треугольника ABC вращением вокруг горизонтали h (рис. 3.31) через точки А₁ и В₁ проведены плоскости вращения α₁ и α₁¹ на следах α₁ и α₁¹,от центров вращения O₁ и О₁¹ отложены радиусы вращения О₁А₀=О₂А₂ и О₁¹В₀= О₂¹В₂.

 

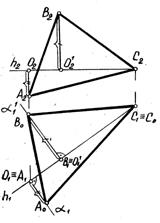
Рис. 3.31.

 

Для большей выразительности и лучшей читаемости чертежа построение натуральной величины сечения рекомендуется выносить на свободное поле чертежа. На рис. 3.32, анаклонная призма пересекается горизонтально проецирующей плоскостью α. Натуральная величина

 

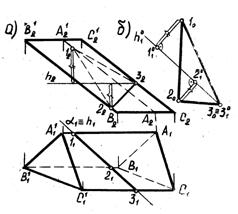
Рис. 3.32.

 

сечения построена на рис. 3.32,б, где h₁⁰||h₁ и расстояния между точка-ми 1₁⁰; 2₁⁰; 3₁⁰ равны расстояниям между точками 1₁; 2₁; 3₁. Из точек 1₁⁰ и 2₁⁰ восстановлены перпендикуляры – следы плоскостей вращения, на которых отложены радиусы вращения. Аналогично на рис. 3.33 определена натуральная величина сечения конуса горизонтально проецирующей плоскостью.

 

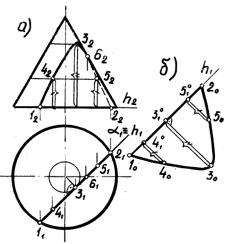
Рис. 3.33.

 

Если фигура сечения расположена во фронтально проецирующей плоскости, то натуральную величину сечения целесообразно определять вращением вокруг фронтали, как это принято делать на чертежах при построении наклонных сечений. На рис. 3.34,а истинный вид A₀B₀C₀ треугольника ABC получен вращением вокруг фронтали f. Точка А неподвижна, так как находится на оси вращения, точка В вращается в плоскости вокруг центра О, а точка С – в плоскости β¹ вокруг центра О¹. Радиусы вращения ОВ и O₁C перпендикулярны П₂ и на П₁ проецируются без искажения. На следе β₂ от центра О₂ отложен радиус вращения r точки В, а на следе β₂¹ от точки О₂¹ – радиус вращения r¹точки С. На рис. 3.34,б определена натуральная величина сечения призмы фронтально проецирующей плоскостью β. Сечение построено на свободном поле чертежа, при этом f₂⁰ f₂ || β₂расстояние между точками 1₂⁰; 2₂⁰; 3₂⁰ равны расстояниям между точками 1₂; 2₂; 3₂, и на перпендикулярах, восстановленных из точек 1₂⁰; 2₂⁰; 3₂⁰ к f₂⁰, отложены отрезки, равные длине радиусов вращения. На рис. 3.34,в таким же способом построена натуральная величина сечения цилиндра, а на рис. 3.34, г – конуса фронтально проецирующей плоскостью.

Нужно иметь в виду, что натуральная величина сечения, занимающего общее положение, может быть определена не только вращением вокруг горизонтали. Для решения этой задачи можно рекомендовать двойную замену плоскостей проекций. На рис. 3.35 таким способом найдена натуральная величина сечения призмы плоскостью. Сначала в плоскости сечения α (1,2,3,4) проведена горизонталь A-3, затем новая ось X₁₄ перпендикулярно A₁З₁. Это обеспечивает переход к новой системе плоскостей проекций П₁/П₄, где плоскость сечения α (1,2,3,4) П₄. Вторая замена состоит в переходе от системы П₁/П₄ к системе П₄/П₅, где X₄₅||α₄(1₄2₄3₄4₄) и α (l,2,3,4)||П₅. Фигура 1₅2₅3₅4₅ является натуральной величиной сечения.

Истинный вид сечения, расположенного произвольно, может быть найден комбинированным способом, как показано на рис. 3.36. На первом этапе заменой плоскости П₂ на П₄ плоскость сечения α (1,2,3,4) преобразована в проецирующую плоскость. На втором же этапе определена натуральная величина сечения α (1₀2₀3₀4₀). Она найдена вращением вокруг фронтали f, совпадающей с большой осью эллипса.

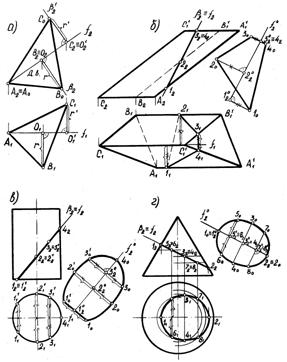
Рис.3.34.

рис. 3.35.

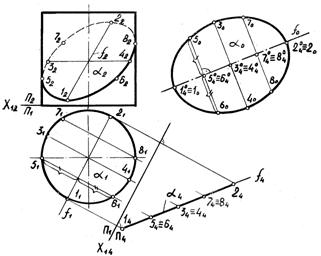
рис.3.36.

Решение 3-й задачи. Разверткой поверхности называется плоская фигура, полученная в результате совмещения всех точек поверхности с одной плоскостью. Все существующие поверхности делятся на развёртываемые и неразвёртываемые. Развёртываемые поверхности совмещаются с плоскостью без разрывов и накладок.

Следует иметь в виду, что ребра многогранников, углы наклона рёбер к сторонам основания, образующие линейчатых поверхностей изображаются на развертке в натуральную величину. Поэтому перед выполнением развёрток следует определить истинную величину ребер или образующих, которые используются в построении развёртки.

Гранные поверхности разворачиваются точно. Развёртка пирамиды выполняется путем последовательного построения ее граней (треугольников). Развертка призмы в общем случае выполняется с использованием нормального сечения. Но если ребра и основание призмы проецируются на плоскости проекций в натуральную величину, то развёртку в этом случае рациональнее выполнять способом раскатки граней призмы до положения, параллельного одной из плоскостей проекций.

Нужно знать, что из кривых поверхностей развёртываемыми являются линейчатые поверхности, у которых две смежные образующие параллельны или пересекаются. Этим условиям отвечают конические и цилиндрические поверхности. Следует обратить внимание, что точно развёртываемые поверхности конуса и цилиндра практически развёртываются снекоторым приближением, так как сначала в конус вписывается пирамида, затем выполняется ее развёртка и через концы ребер проводится плавная кривая линия. Цилиндрическая поверхность разворачивается аналогично. Предварительно в заданный цилиндр вписывается призма, которая затем разворачивается и через концы ребер проводится плавная кривая линия. Неразвёртываемые поверхности разворачиваются приближенно.

Решение 4-й задачи. Фигуру следует выполнить в прямоугольной изометрии или в прямоугольной диметрии. Выбор вида аксонометрии должен обеспечивать хорошую наглядность изображения, чтобы грани многогранника не проецировались в прямые линии, а ребра не проецировались в точки, чтобы одни элементы поверхности меньше закрывали другие. Лучше выполнять увеличенное наглядное изображение с более простыми для построения приведенными коэффициентами. В изометрии по всем осям коэффициенты равны единице, в диметрии по осям ОХ и OZ – единице, а по оси ОУ – 0,5.

Построение аксонометрических проекций основано на параллельном проецировании. Поэтому на наглядном изображении сохраняется параллельность взаимно параллельных в пространстве линий.

При построении аксонометрии необходимо учитывать, что окружности, расположенные в плоскостях П₁, П₂, П₃ и в плоскостях им параллельных, на наглядном изображении преобразуются в эллипсы, которые выполняются по восьми точкам, либо иным известным способом. Малая ось каждого эллипса параллельна той из осей ОХ, ОУ или OZ, которая не лежит в плоскости окружности. Две точки определяет малая ось, которая является проекцией диаметра окружности, получившего наибольшее сокращение. В изометрии малая ось эллипса равна 0,71d. В диметрии для окружностей, расположенных в П₁ и П₃, малая ось эллипса равна 0,35d, a в П₂ – 0,94d. Две другие точки определяет большая ось эллипса, которая равна визометрии l,22d, а в диметрии – 1,06d. Остальные четыре точки определяются проекциями тех диаметров окружности, которые параллельны осям ОХ, ОУ или OZ. Длина проекций этих диаметров зависит от величины коэффициентов искажения по аксонометрическим осям, которым они параллельны. Построение эллипсов по восьми точкам в изометрии и диметрии показано на рис. 3.37.

 

Рис. 3.37.

 

Начинать построение аксонометрической проекции следует с проведения координатных осей на ортогональных проекциях и аксонометрических осей на свободном поле формата. Затем на ортогональном чертеже определяются координаты точек и с учетом коэффициентов искажения по осям строятся аксонометрические проекции этих точек. Для гранных поверхностей такими точками являются вершины, через которые проводятся ребра и стороны оснований. Таким же приемом наносится линия сечения на многограннике. Построение упрощается, если использовать взаимную параллельность ребер или соответственных сторон оснований.

На аксонометрической проекции конуса и цилиндра контурами оснований являются эллипсы. Очерковые образующие конуса и цилиндра касаются оснований. Линия сечения на кривой поверхности проходит через аксонометрические проекции особых и общих точек. Пример построения диметрической проекции приведен на рис. 3.21.

Эпюр № 3

 

В эпюр 3 включены две задачи, решение которых предполагает построение трёх проекций заданных тел и проекций линий пересечения поверхностей этих тел. Условия обеих задач идентичны.

Заданы по две проекции первого и второго геометрических тел. Тела имеют такое взаимное расположение, что поверхности этих тел пересекаются.

Задача 1. Построить все три проекции контуров двух разнотипных геометрических тел. Найти проекции точек, общих для поверхностей этих тел. Построить проекции линии пересечения поверхностей, определив видимые и невидимые части линии.

Задача 2. Построить все три проекции контуров двух однотипных геометрических тел – тел вращения, имеющих общую точку пересечения осей этих тел. Найти точки, общие для поверхностей обоих тел, и построить проекции линии пересечения поверхностей.

Задание выполняется на двух листах формата A3 (297´420). Данные для выполнения эпюра взять из индивидуального задания. Проекции линии взаимного пересечения поверхностей выполнить цветным карандашом.

Перед тем как приступить к решению задач эпюра 3, следуетповторить предшествующие темы курса начертательной геометрии на пересечение поверхностей плоскостью и прямой линией. Нужно четко представлять, что цилиндрическая поверхность может пересекаться плоскостью по образующим, эллипсу или окружности; коническая – по образующим, окружности, эллипсу, параболе или гиперболе; сферическая – только по окружностям и т. д. Изучитьв рекомендуемой литературе тему на взаимное пересечение поверхностей, проработать выполненные варианты решений аналогичных задач.

Решение задач. Прежде чем приступить к решению задач, нужно изучить и представить заданные взаимно пересекающиеся поверхности. Следует учитывать, что в зависимости от вида поверхностей решение задачи имеет свои особенности.

Так, гранные, т.е., составленные из фрагментов плоскостей, поверхностипересекаются по плоской или пространственной ломаной линии, которая определяется вершинами – точками пересечения ребер одной поверхности с гранями второй и ребер второй с гранями первой. На рис. 3.38 ребра наклонной призмы пересекаются с гранями прямой призмы в точках 1, 2, 4, 6, а ребра прямой призмы пересекают грани наклонной в точках 3 и 8, 5 и 7. Полученные точки последовательно соединены. В данном случае задача сводится к известной задаче на пересечение прямой линии с плоскостью.

Задачи, в которых предполагаемые взаимопересекающиеся поверхности являются поверхностями второго либо более высокого порядка (цилиндрические, конические, сферические, торовые и др.), решаются способом вспомогательных поверхностей посредников – секущих плоскостей.

Алгоритм решения задачи:

1) вводится вспомогательная плоскость-посредник;

2) строится линия пересечения вспомогательной плоскости и одной из заданных поверхностей;

 

 

рис. 3.38.

 

3) строится линия пересечения плоскости-посредника и второй заданной поверхности;

4) определяются точки пересечения полученных линий по пунктам 3 и 4. Точек может быть от одной до четырех в зависимости от взаимного расположения заданных поверхностей и вспомогательной плоскости.

Затем вводится другая вспомогательная плоскость, и алгоритм повторяется до тех пор, пока не будет определено достаточное количество точек. Полученные точки соединяются плавной кривой линией. Вначале обычно определяются «особые», или «опорные» точки. Это – «низшая» и «высшая», точки «видимости» и др.

При выборе вспомогательных плоскостей следует помнить, что они должны пересекать обе заданные поверхности по простейшим линиям – окружностям или отрезкам прямых. Выбираются обычно плоскости уровня: горизонтальные или вертикальные, или те и другие.

На рис. 3.39 «высшая» точка 1 и «низшая» 2 определяются пересечением очерковой образующей конуса и очерковой окружности сферы, расположенных в фронтальной плоскости s. Точки «видимости» 3 и 4 получены введением горизонтальной плоскости уровня g, которая пересекает конус и сферу по окружностям. Общие точки 5 и 6 определены введением вспомогательной горизонтальной плоскости уровня b. Полученные точки соединены плавной кривой линией. Две точки (3 и 4) делят горизонтальную проекцию линии пересечения на видимую и невидимую части. На фронтальной плоскости проекций невидимая часть линии пересечения совпадает с видимой частью.

Рис. 3.39. Рис. 3.40.

Следует обратить внимание, что в задачах на пересечение кривых и гранных поверхностей линия пересечения поверхностей состоит из отдельных плоских кривых или прямых линий. Это зависит от того, по какой линии грани многогранника пересекают кривую поверхность и как эти линии пересечения проецируются на плоскости проекций. Так, на рис. 3.40 грани пирамиды пересекают цилиндр по эллипсам.

На рис. 3.41 призма пересекается с конусом. Грань призмы aпересекает конус по образующим 1, 2 и 3, 4, грань g – по гиперболе 1, 8, 7, 9, 6. Верхнее основание призмы b пересекает ко­нус по эллипсу 2, 5, 4.

На рис. 3.42 горизонтальная проекция линии пересечения совпадает с проекцией призмы, а фронтальная проекция получена при помощи окружностей второй, непроецирующей поверхности – сферы.

На рис. 3.43 сферическая поверхность пересекается призмой по дугам окружностей, одна из них (1–3) проецируется на П₂ в натуральную величину, две другие (1, 8, 6, 4, 9, 2 и 2, 10, 5, 7, 11, 3) – в полуэллипсы.

 

Рис. 3.41. Рис. 3.42.

Эти задачи могут быть решены способом секущих плоскостей. На рис. 3.40 для решения задачи использованы вспомогательные горизонтальные плоскости, которые пересекают призму по треугольникам, подобным основанию, а цилиндр – по образующим.

Следует обратить внимание на решение тех задач, в которых одна из заданных взаимно пересекающихся поверхностей является проецирующей. В таких случаях одна проекция линии пересечения поверхностей известна. Она совпадает с проекцией проецирующей поверхности. Для определения недостающей проекции линии пересечения могут быть использованы линии(окружности или образующие) второй непроецирующей поверхности.

На рис. 3.41 проецирующая поверхность – призма, непроецирующая – конус. Для определения недостающих проекций линий пересечения использованы окружности и образующие конуса.

Особую группу задач на определение линии взаимного пересечения составляют задачи с поверхностями вращения. Такие задачи рациональнее решать способом концентрических сфер. В этом случае используется то, что сфера, центр которой расположен на оси поверхности вращения конуса, цилиндра, пересекает поверхности по окружностям. Эти окружности проецируются в прямые линии, если оси поверхностей вращения параллельны плоскости проекций.

На рис. 3.43 окружности проецируются в прямые линии на П₂. Чтобы вспомогательная сфера пересекала обе поверхности вращения по окружностям, следует точку пересечения осей этих поверхностей при­нять за центр концентрических вспомогательных сфер. Наибольшая сфера должна проходить через самую удаленную от центра точку пересечения очерковых линий заданных поверхностей вращения. Наименьшая из вспомогательных сфер должна касаться одной поверхности вращения и пересекать другую.

 

Рис. 3.43.

 

Следует помнить, что проницание пересекающихся поверхностей зависит от того, какой поверхности касается наименьшая сфера. На рис. 3.44,а наименьшая сфера касается конуса и пересекает цилиндр. В этом случае цилиндр проницает конус. На рис. 3.44,б наименьшая из сфер касается цилиндра и пересекает конус. Здесь, наоборот, конус проницает цилиндр. Проницает та поверхность, которая пересекается наименьшей сферой.

При построении проекций линии пересечения поверхностей следует исходить из того, что видимая часть линии взаимного пересечения поверхностей должна быть расположена на видимой (обозреваемой) части одной и второй поверхностей. Точки, разделяющие видимую и невидимую части линии пересечения, находятся на очерковых линиях пересекающихся поверхностей.

 

Рис. 3.44.

 

Примеры выполнения эпюра № 3 даны на рис. 3.45. и 3.46.

На рис.3.45 построены проекции линии пересечения поверхности трёхгранной наклонной призмы с поверхностью прямого кругового цилиндра. Построение осуществлялось с помощью вспомогательных секущих плоскостей.

На рис.3.46 выполнено построение проекций линии пересечения прямого кругового усеченного конуса с прямым круговым цилиндром. Здесь линия пересечения найдена с помощью вспомогательных концентричных сфер.

 

 

 

ЛИТЕРАТУРА

 

1. Г о р д о н, О. В. Курс начерта­тельной геометрии./О.В. Гордон, М.А. Семенцов-Оглевский. М.: Высш.шк., 2000. 272 с.

2. К р ы л о в, Н. Н. Начертательная геометрия./Н.Н. Крылов. М.: Высш. шк., 2002. 231 с.

3. К у з н е ц о в, Н. С. Начертательная геометрия. /Н.С. Кузнецов. М.: Высш. шк., 1991. 262 с.

4. Д р ж е в е ц к и й, В.В. Основы начертательной геометрии и проекционное черчение. /В.В. Држевецкий. под ред. Л.С. Шабеки. Минск: Дизайн ПРО, 2000. 112 с.