Лекция 3. Нахождение функции отклика и определение меры согласованности между величинами в двухфакторном эксперименте.

Результаты двух факторного эксперимента могут быть представлены следующей таблицей:

			...
			...
			...

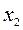
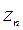
В общем случае, зависимость значений отклика от значений фактора и значений фактора описывается формулой:

(1)

Чтобы выбрать вид зависимости (другими словами, указать, какие слагаемые в общей формуле следует оставить) полученные данные анализируют. Составляют корреляционную таблицу для величин и . Пользуясь таблицей, для каждого значения находят средние значения и эти точки отмечают на координатной плоскости. По расположению точек делают вывод о наличии линейной, квадратичной, кубической или другого вида зависимости от . Аналогичным образом устанавливают вид зависимости от . После этого в формуле (1) оставляют нужное количество слагаемых. Числовые параметры выбранной зависимости находят с помощью метода наименьших квадратов.

Распространённым случаем является наличие линейной зависимости отклика от обоих факторов:

.

Числовые параметры этой зависимости найдём из системы, составленной применением метода наименьших квадратов:

(2)

Пример. В таблице представлены результаты изучения влияния изменения объёма промышленного производства и среднедушевого дохода на товарооборот. Для этого по 20 регионам РФ были получены следующие данные.

Нужно найти уравнение зависимости отклика (розничного товарооборота) от факторов (объёма промышленного производства) и (среднедушевого денежного дохода).

Чтобы выбрать вид зависимости проанализируем полученные данные. Составим корреляционную таблицу для величин и :

Пользуясь таблицей, для каждого значения найдём средние значения :

95,5

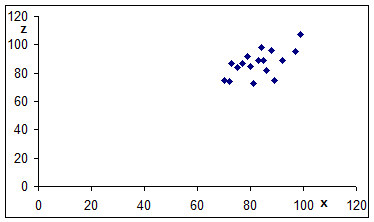
Нанесём полученные данные на координатную плоскость.

Расположение точек указывает на линейную зависимость между и .

Составим теперь корреляционную таблицу для величин и .

Найдём соответствующие средние значения величины для каждого значения величины :

87,5

Отложим полученные данные на координатной плоскости.

По расположению точек выбираем линейную зависимость между и .

Таким образом, общая формула зависимости величины от величин и будет иметь вид:

.

Найдя необходимые суммы, подставим их в систему (2):

Решая её, найдём уравнение зависимости:

.

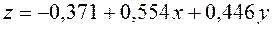Для проверки полученной формулы для каждой пары значений и , представленных в таблице, вычислим по ней значения (округлив их до целых) и сравним с имеющимися в таблице.

№
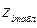
					– 3
					– 1
					– 4
					– 1
					– 4
					– 11
					– 3
					– 6
					– 3
					– 7
					– 1

Результаты, представленные в таблице, показывают, что отклонения вычисленных значений от табличных небольшие: намного меньше самих значений, а их сумма практически равна нулю. Таким образом, можно признать, что полученная формула адекватно описывает статистические данные.

Оценим тесноту связи между величинами. В случае линейной зависимости это можно сделать, вычислив парные коэффициенты корреляции:

коэффициент корреляции между и ;

коэффициент корреляции между и ;

коэффициент корреляции между и .

В приведённых формулах использованы следующие обозначения:

; ; ; ; ; ;

; ; .

Используя уже найденные суммы и вычислив , найдём:

, ; .

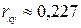Также можно вычислить частные коэффициенты корреляции, которые характеризуют тесноту связи между откликом и каким-либо фактором при фиксированном воздействии другого фактора:

; .

Для рассматриваемого примера эти коэффициенты будут равны:

, .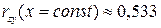