Площадь криволинейной трапеции. Пусть на плоскости  дана фигура, ограниченная отрезком
дана фигура, ограниченная отрезком  оси
оси  . прямыми
. прямыми  ,
,  и графиком непрерывной
и графиком непрерывной

|
Рис. 2.
И неотрицательной функции 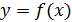 на
на  . Такую фигуру, как мы знаем, называют криволинейной трапецией, площадь
. Такую фигуру, как мы знаем, называют криволинейной трапецией, площадь  которой может быть вычислена по формуле (1')
которой может быть вычислена по формуле (1')

Итак, определенный интеграл от неотрицательной непрерывной функции  на
на  численно равен площади криволинейной трапеции с основанием
численно равен площади криволинейной трапеции с основанием  , ограниченной сверху графиком функции
, ограниченной сверху графиком функции 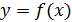 . В этом заключается геометрический смысл определенного интеграла.
. В этом заключается геометрический смысл определенного интеграла.
Пример 1. (из тетради)

Рис. 3.
Пусть фигура ограничена снизу и сверху графиками функций  ,
,  и
и  ,
,  (рис. 94), где
(рис. 94), где  ,
,  — две непрерывные функции. Если обе функции неотрицательны, то площадь данной фигуры является разностью площадей криволинейных трапеций, ограниченных сверху соответственно графиками функций
— две непрерывные функции. Если обе функции неотрицательны, то площадь данной фигуры является разностью площадей криволинейных трапеций, ограниченных сверху соответственно графиками функций  ,
,  , прямыми
, прямыми  ,
,  и осью
и осью  . Следовательно, площадь
. Следовательно, площадь  данной фигуры равна
данной фигуры равна

Заметим, что формула (3) справедлива и тогда, когда  и
и  неположительны, так как в силу их ограниченности существует число
неположительны, так как в силу их ограниченности существует число  такое, что функции
такое, что функции

становятся неотрицательными и имеет место очевидное равенство
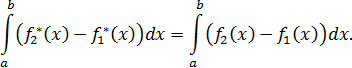
Пример 2. (из тетради)
Замечание. При вычислении площади криволинейной трапеции в случае, когда верхняя граница задана параметрическими уравнениями  ,
,  ,
,  , в формуле (1') надо сделать замену переменной, положив
, в формуле (1') надо сделать замену переменной, положив  ,
,  . Тогда получим
. Тогда получим

где  и
и  — значения параметра
— значения параметра  , соответствующие значениям
, соответствующие значениям  и
и  т.е.
т.е.  ,
,  .
.
Пример 3. Вычислить площадь фигуры, ограниченной эллипсом
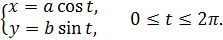
Решение. Ввиду симметрии данной кривой относительно осей координат достаточно вычислить площадь части фигуры, находящейся в первой четверти

|
Рис. 4.
Следовательно, искомая площадь равна

Площадь криволинейного сектора. Пусть кривая  задана в полярных координатах уравнением
задана в полярных координатах уравнением

Рис. 5.

причем функция  непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке  . Плоскую фигуру, ограниченную кривой
. Плоскую фигуру, ограниченную кривой  и двумя полярными радиусами, составляющими с полярной осью углы
и двумя полярными радиусами, составляющими с полярной осью углы  и
и  , мы будем называть криволинейным сектором (рис. 5). Площадь
, мы будем называть криволинейным сектором (рис. 5). Площадь  криволинейного сектора может быть вычислена по формуле
криволинейного сектора может быть вычислена по формуле

Пример 4. Вычислить площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда  , где
, где  — положительное число (рис. 6).
— положительное число (рис. 6).

Рис. 6.
Решение. Когда  изменяется от 0 до
изменяется от 0 до  , то полярный радиус
, то полярный радиус  описывает кривую, ограничивающую криволинейный сектор
описывает кривую, ограничивающую криволинейный сектор  . Поэтому по формуле (4) имеем
. Поэтому по формуле (4) имеем

Заметим, что точка  отдалена от полюса на расстояние
отдалена от полюса на расстояние  . Поэтому круг радиуса
. Поэтому круг радиуса  имеет площадь
имеет площадь

т.е. площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда, равна 1/3 площади круга с радиусом, равным наибольшему из полярных радиусов витка. К этому выводу пришел еще Архимед.
Длина дуги кривой. Пусть плоская кривая  задана уравнением
задана уравнением 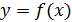 ,
,  , где
, где  — непрерывная функция на отрезке
— непрерывная функция на отрезке  . Разобьем кривую
. Разобьем кривую  на
на  произвольных частей точками
произвольных частей точками  в направлении от
в направлении от  к
к  . Соединив эти точки хордами, получим некоторую вписанную ломаную линию, периметр которой обозначим через
. Соединив эти точки хордами, получим некоторую вписанную ломаную линию, периметр которой обозначим через 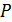 (рис. 7). Через
(рис. 7). Через  обозначим длину одного звена
обозначим длину одного звена  ломаной линии, а через
ломаной линии, а через  — длину наибольшего из ее звеньев:
— длину наибольшего из ее звеньев:  .
.

Рис. 7.
Определение. Число  называется пределом периметров
называется пределом периметров 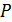 при
при  , если для любого
, если для любого  существует
существует  такое, что для всякой ломаной, у которой
такое, что для всякой ломаной, у которой  , выполняется неравенство
, выполняется неравенство

Если существует конечный предел  периметра
периметра 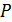 вписанной в кривую ломаной линии при
вписанной в кривую ломаной линии при  , то этот предел называется длиной дуги
, то этот предел называется длиной дуги  :
:

Если функция  непрерывна вместе с
непрерывна вместе с  на отрезке
на отрезке  , то длина дуги
, то длина дуги  выражается формулой
выражается формулой

Пример 5. Вычислить длину дуги верхней ветви полукубической параболы  от
от  до
до  .
.

Замечание 1. При вычислении длины дуги в случае, когда кривая  задана параметрическими уравнениями
задана параметрическими уравнениями

где  и
и  — значения параметра
— значения параметра  , соответствующие значениям
, соответствующие значениям  и
и  , т. е.
, т. е.  ,
,  , в формуле
, в формуле

надо сделать замену переменной, положив  ,
,  . Тогда получим
. Тогда получим

Пример 6. Вычислить длину дуги одной арки циклоиды[1]:  ,
,  ,
,  .
.

Решение. Из уравнения циклоиды находим, что 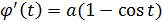 ,
,  . Когда
. Когда  пробегает отрезок
пробегает отрезок  , параметр
, параметр  пробегает отрезок
пробегает отрезок  . Следовательно, искомая длина дуги равна
. Следовательно, искомая длина дуги равна

Замечание 2. При вычислении длины дуги в случае, когда кривая  задана в полярных координатах уравнением
задана в полярных координатах уравнением  ,
,  , где
, где  имеет непрерывную производную
имеет непрерывную производную  на отрезке
на отрезке  и точкам
и точкам  и
и  соответствуют значения
соответствуют значения  и
и  , переходя от полярных координат к прямоугольным, получим параметрическое задание кривой
, переходя от полярных координат к прямоугольным, получим параметрическое задание кривой  уравнениями
уравнениями  ,
,  с параметром
с параметром  . Тогда
. Тогда

и формула (6) принимает вид: (7)

где  и
и  — значения параметра
— значения параметра  .
.
Пример 7. Вычислить длину первого витка архимедовой спирали  .
.
Решение. Первый виток архимедовой спирали образуется при изменении полярного угла ф от 0 до  . Тогда по формуле (7) искомая длина дуги равна …
. Тогда по формуле (7) искомая длина дуги равна …
Объем тела вращения. Пусть функция  непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке  . Тогда тело, образованное вращением вокруг оси
. Тогда тело, образованное вращением вокруг оси  криволинейной трапеции, ограниченной сверху графиком функции
криволинейной трапеции, ограниченной сверху графиком функции  , имеет объем
, имеет объем  , который может быть найден по формуле
, который может быть найден по формуле
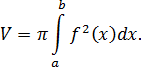
Пример 8. Вычислить объем тора. Тором называется тело, получающееся при вращении круга радиуса  вокруг оси, лежащей в его плоскости на расстоянии
вокруг оси, лежащей в его плоскости на расстоянии 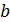 от центра (
от центра ( ). Форму тора имеет, например, баранка.
). Форму тора имеет, например, баранка.
Решение. Пусть круг вращается вокруг прямой  .
.
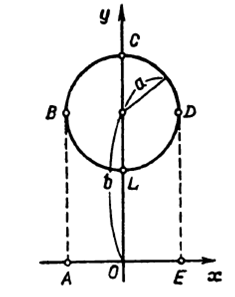
Тогда объем тора может быть рассмотрен как разность объемов вращения криволинейных трапеций 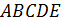 и
и  вокруг оси
вокруг оси  .
.
Если оси координат выбрать, как показано на рис., то уравнение окружности  будет иметь вид
будет иметь вид

где  — радиус круга, причем уравнение кривой
— радиус круга, причем уравнение кривой 

а уравнение кривой 

Тогда объем тора будет равен

Площадь поверхности вращения. Пусть функция  неотрицательна и непрерывна вместе со своей первой производной на отрезке
неотрицательна и непрерывна вместе со своей первой производной на отрезке  . Тогда поверхность, образованная вращением графика этой функции вокруг оси Ох, имеет площадь
. Тогда поверхность, образованная вращением графика этой функции вокруг оси Ох, имеет площадь 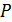 , которая может быть вычислена по формуле (8)
, которая может быть вычислена по формуле (8)

Замечание. Если поверхность получается путем вращения вокруг оси  кривой
кривой  , заданной параметрическими уравнениями
, заданной параметрическими уравнениями  ,
,  ,
,  , причем
, причем  ,
,  изменяется от
изменяется от  до
до 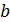 при изменении
при изменении  от
от  до
до  , то, осуществляя в интеграле (8) замену переменной по формулам
, то, осуществляя в интеграле (8) замену переменной по формулам  ,
,  получим (9)
получим (9)

Наконец, если кривая задана уравнением в полярных координатах  ,
,  , где
, где  имеет непрерывную производную на
имеет непрерывную производную на  , то этот случай с помощью формул перехода
, то этот случай с помощью формул перехода  ,
,  приводится к параметрической форме задания кривой, и формула (10) принимает вид
приводится к параметрической форме задания кривой, и формула (10) принимает вид

Пример 9. Вычислить площадь 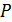 поверхности шара радиуса
поверхности шара радиуса  .
.
Решение.  .
.
Пример 10. Вычислить площадь 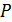 поверхности, полученной вращением циклоиды
поверхности, полученной вращением циклоиды  ,
,  ,
,  вокруг оси
вокруг оси  .
.
Решение.

Вычисление моментов.
Если на прямой  масса
масса  плотности
плотности  заполняет отрезок
заполняет отрезок  , то
, то  ым моментом массы
ым моментом массы  называется число
называется число

Как частные случаи получаем при 
 — массу, при
— массу, при  — статический момент, при
— статический момент, при  — момент инерции.
— момент инерции.
[1] Циклоида — плоская кривая, которую описывает точка М окружности радиуса а, катящейся без скольжения по прямой линии.