Костюков Вячеслав Михайлович. Зав. каф. 303 МАИ. Доктор технических наук, профессор. Телефон: 8-910-477-30-11. e-mail: kost_slv@mail.ru
Нгуен Ньы Ман. Аспирант МАИ. Телефон: (499) 158-42-16.
Статья является продолжением статьи авторов, опубликованной в предыдущем номере.
В статье обсуждается вопрос о влиянии погрешностей измерений бароинерциальной системы, не полностью скомпенсированных в бортовом алгоритме ИВК на точность навигации самолета. Полученные результаты позволяют формировать требования к точности калибровки, обеспечивающие заданную точность движения самолета.
Алгоритм реализует моделирование движения самолета в неинерциальной (нормальной Земной) системе координат (СК) в соответствии с полетным заданием, состоянием среды движения (с вариациями атмосферы), используя общие нелинейные модели характеристик самолета, систему управления, содержащую алгоритм оптимального управления самолетом для поиска требуемых траекторий и законов управления, алгоритм стабилизации и балансировки самолета, измерительно-вычислительный комплекс на базе гироинерциального блока, баровысотомера и БЦВМ.
Ключевые слова: пространственное движение, тяжелый беспилотный самолет, разбег, набор высоты, маршрут, бароинерциальная система измерения, точность измерения вектора состояния самолета.
1. Моделирование работы инерциального блока системы измерения и модуля обработки первичных информаций
1.1. Алгоритм работы инерциального блока системы измерения
Входными сигналами в модель инерциальной системы измерения являются угловые скорости самолета 
и линейные ускорения 
в проекциях на оси связанной с самолетом системы координат (ССК) О1Х1Y1Z1, поступающие из его модели движения.
|
|
Гиро-инерциальный блок и связанная с ним приборная система координат (ПСК) отклонены на некоторые углы относительно связанной с корпусом самолета системы координат О1X1Y1Z1, поэтому измеряемые линейные ускорения и угловые скорости отличаются от их фактических значений:
где 
– компоненты измеряемого ускорения в ПСК; 
- проекции ускорения от аэродинамических сил и силы тяги двигателя на оси ССК самолета; 
- компоненты вектора абсолютной угловой скорости в ПСК; 
- проекции вектора абсолютной угловой скорости самолета на оси ССК; 
- элементы матриц перехода от ПСК в ССК.
С учетом дрейфа, изменения масштабных коэффициентов и других факторов измеряемые линейные ускорения самолета, полученные на выходе измерительной системы определяются выражениями (в виде количества импульсов)[8]:
где 
– цена импульса; 
- смещения нуля; 
- отклонение масштабных коэффициентов;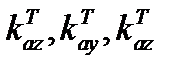 
- температурный коэффициент изменения смешения нуля; 
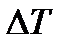- отклонение текущей температуры акселерометра от температуры его калибровки,
а измеряемые угловые скорости - выражениями:
где 
– цена импульса; 
- смещения нуля; 
- коэффициент линейной составляющей смещения нуля; 
- отклонение масштабного коэффициента от своего среднеквадратического значения; 
- температурный коэффициент изменения; 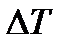- отклонение текущей температуры гироскопа от температуры его калибровки; 
– время работы.
1.2. Алгоритм обработки информации с гиро-инерциального блока системы измерения
Измеренные линейные ускорения 
и угловые скорости 
, поступающие от акселерометров (ДЛУ) и гироскопов (ДУС) в модуль обработки информации, обрабатываются по формулам:
|
|
и
где 
- используемые в алгоритме навигации векторы линейных ускорений и угловых скоростей в связанной СК.
В данной работе считаем, что температурная стабилизация гироблока обеспечена. Поэтому изменением температуры гироблока относительно температуры калибровки пренебрегаем, т.е. 
.
Ниже приведены некоторые варианты моделирования движения самолета с инерциальной системой измерения, имеющей неточность калибровки (0%, 1%, 2%). Для этого к каждому перечисленному выше коэффициенту, соответствующему точной калибровке (используемому для моделирования измеряемых линейных ускорений и угловых скоростей) необходимо добавить соответствующую величину, характеризующую неточность его определения при калибровке. Это иллюстрируется блок-схемой (рис. 8.), в которой показано, что перед передачей паспортных данных датчиков в модуль измерения производиться «искажение» их значений путем добавления к ним неточности калибровки (k % от рассчитанного при калибровке значения). Вследствие этого, после восстановления в модуле обработки информации поступающих от модуля измерения значений угловых скоростей и линейных ускорений, получим приращения углов и скоростей отличающиеся от действительных (по моделированию движения самолета) значений на величину, зависящую от k.
Рис. 8. Блок-схема алгоритма моделирования работы измерительной системы.
2. Моделирование работы баровысотомера
Модель баровысотомера и модель его ошибок, используемая в данной работе аналогичны [7]: 
,
|
|
где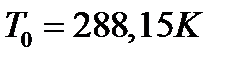 
- температура воздуха на нулевой высоте; 
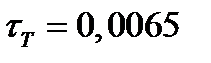- градиент изменения температуры с изменением высоты; 
- измеренное статическое атмосферное давление; 
- статическое атмосферное давление на нулевой высоте; 
м/град - универсальная газовая постоянная.
Погрешности определения высоты:
; 
,
где eбв = 0.1 м – постоянная погрешность в начале движения; sбв =10 м – СКО коррелированной ошибки; 
= 200 с – период корреляции; w – белый шум единичной интенсивности.
3. Алгоритм навигации
3.1. Общий алгоритм инерциальной навигации
Общий алгоритм инерциальной инерции состоит из двух алгоритмов – алгоритма вычисления углов ориентации и алгоритма вычисления скорости и координат. Он представлен на рис. 9, аналогичен [8]:
Рис. 9. Блок-схема общего алгоритма навигации.
где 
- векторы линейных ускорений и угловых скоростей самолета в ССК; 
- приращения вектора скорости и углов за интервал времени 
; 
- расчетный вектор ускорения силы тяжести; 
- вектор коррекций приращения скорости по вращению Земли; 
- вектор коррекций приращения углов по вращению Земли.
3.2. Алгоритм вычисления углов ориентации
Рассмотрим алгоритм с использованием кватерниона для определения углов ориентации. Кватернион вектор:
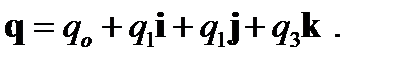
Матрица перехода от связанной СК в навигационную СК имеет вид:
Углы Эйлера в этом случае определяются соотношениями:
Во время работы инерциальной навигации кватернион q вычисляется по следующей формуле:
(2)
где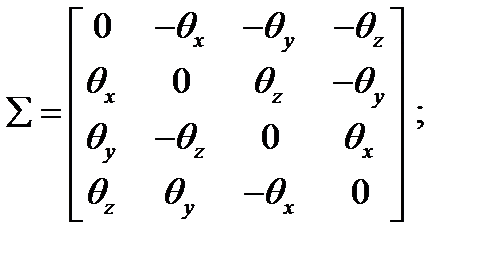 
q k, q k+1 – кватернион поворота самолета в момент времени tk и tk+1; 
- приращение углов за ; 
- такт работы алгоритма навигации, 
.
При реализации алгоритма (2) на БЦВМ с целью повышения частоты обработки информации используем следующую приближенную формулу [9]:
где
3.3. Алгоритм определения координат
Формула для вычисления приращения вектора скоростей самолета за интервал времени от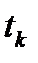 
до 
относительно навигационной СК (без учета коррекции):
(3)
где a – вектор измеренных линейных ускорений самолета в ССК; 
- вектор измеренных угловых скоростей самолета в ССК; 
- вектор кажущегося приращения скорости в ССК; 
– вектор кажущегося поворота самолета в ССК;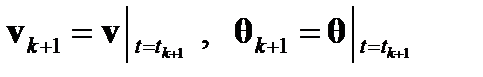 
- приращения вектора скоростей и вектора угла поворота самолета за интервал времени 
.
Для вычисления интегрального члена в (3) используем численный алгоритм, описанный в [8], в итоге получаем формулу для нахождения приращения вектора скорости в навигационной СК за интервал времени 
:
где 
, 
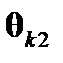- вектор кажущегося поворота за первую и вторую половину интервала 
; 
, 
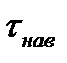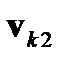- вектор кажущегося приращения скорости за первую и вторую половину интервала 
; 
, 
- вектор кажущегося поворота и вектор кажущегося приращения скорости за вторую половину интервала предыдущего шага.
Координаты самолета определяются интегрированием полученных приращений вектора скорости:
4. Алгоритм комплексной обработки измеренной информации по вертикальному каналу
Так как определение высоты полета 
и вертикальной составляющей скорости 
по показаниям инерциальной системы является неустойчивым вычислительным процессом на относительно длительных интервалах времени (больших 10 минут [6]), для обеспечения точности управления движением самолета используем способ, основанный на совместной обработке измерений инерциальной системы 
и баровысотомера 
- алгоритм бароинерциального фильтра. Алгоритм реализуем как дискретный фильтр Калмана (ДФК) (подобно [7]):
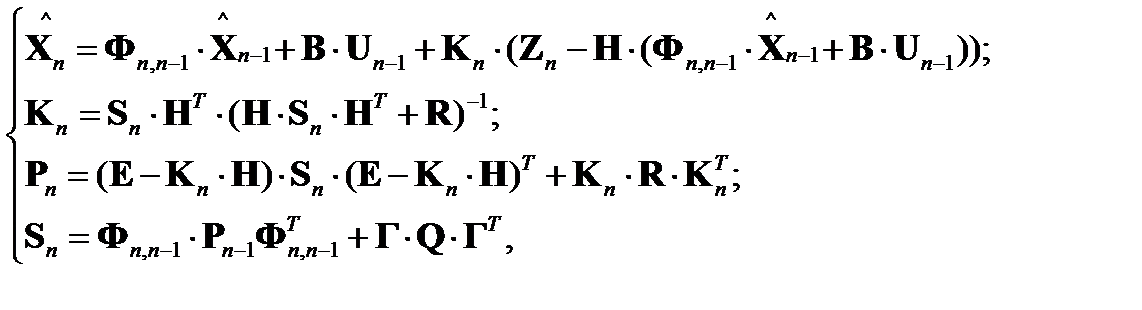
где 
– оценка вектора состояния 
на n-ом интервале времени; 
– значение вектора управления 
на (n-1)-ом интервале времени; 
– значение вектора измерений 
на n-ом интервале времени; 
– значение переходной матрицы состояния 
на n-ом интервале времени; 
– матрица коэффициентов управления; 
– матрица наблюдения; 
– матрица весовых коэффициентов для формирующих шумов; 
– матрица интенсивностей измерительных шумов; 
– матрица интенсивностей формирующих шумов;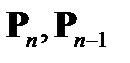 
– априорная ковариационная матрица на n-ом и (n-1)-ом интервале времени; 
– апостериорная ковариационная матрица на n-ом интервале времени; 
– коэффициент усиления фильтра на n-ом интервале времени.
Непрерывные модели процесса и измерения в общем виде представляются следующими выражениями:
где 
- вектор формирующих шумов; 
- вектор шумов измерений;
.
При синтезе алгоритма фильтра было принято, что формирующие шумы 
и шумы измерений 
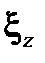являются независимыми центрированными гауссовыми дискретными белыми шумами.
Дискретные модели процесса и измерения представляются следующим образом:
Вектор состояния в данном случае имеет вид: 
где 
- высота полета; 
- вертикальная скорость.
Вектор управляющих воздействий в структуре ДФК в данном случае имеет вид: 
где 
- сигнал вертикального ускорения из алгоритма инерциальной навигации.
Модель измерений строится на основе сигналов баровысотомера:
где 
- текущее измерение высоты; 
- шум измерения высоты.
Матрица наблюдения имеет вид: 
.
Переходная матрица состояния в данном случае имеет следующий вид:
где 
- шаг дискретизации (счета) фильтра, 
.
Матрицы весовых коэффициентов управления имеет вид:
.
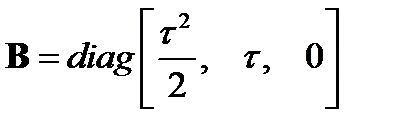Матрица весовых коэффициентов формирующих шумов имеет следующий вид: 
.
5. Результаты моделирования
Полёт самолета смоделирован по следующему полетному заданию:
- широта, долгота точки начала полосы ВПП 
и курсовой угол ВПП 
;
- полет по прямой по направлению Запад- Восток;
- высота и скорость в конечной точке: 
.
В соответствии с этим продолжительность полёта составляет 1367 секунд, а дальность полета - 276 км.
На рис. 10 показан типичный результат моделирования взлета при точной калибровке. Моделирование осуществляется со следующими параметрами алгоритма:
а) 
б) 
в) 
г) 
д) 
е) 
ж) 
Рис. 10. Типичный результат моделирования взлета.
а) – Зависимость дальности полета 
от времени; б) – Зависимость высоты полета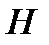 
от времени; в) – Зависимость бокового смещения полета 
от времени; г) – Зависимость скорости самолета 
от времени; д) – Зависимости угла курса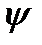 
и угла скольжения 
самолета от времени; ж) – Зависимости угла тангажа 
и угла атаки 
от времени; е) – Зависимость угла крена 
от времени.
В данной работе для моделирования гиро-инерциального блока использованы ДЛУ и ДУС, параметры которых заданы в табл. 3.
В табл. 4. приведены результаты некоторых вариантов моделирования взлета при абсолютно точной калибровке инерциального блока системы измерения.
В табл. 5. приведены результаты моделирования при неточной калибровке по каждому отдельному параметру калибровки датчиков инерциального блока и одновременному отклонению от идеальной калибровки по всем параметрам (для анализа взаимокорреляции ошибок).
Табл. 3. Параметры датчиков исходные для моделирования модуля измерений.
| ДЛУ | ДУС | ||||||
| Параметры калибровки Оси | Смещение нуля 10-3g | Погрешность масштабного коэффициента % | Неортого-нальность датчиков рад. | Постоянная составляющая смещения нуля град./ч | Коэффициент линейной составляющей смещения нуля (град./ч)/с | Погрешность масштабного коэффициента % | Неортого-нальность датчиков рад. |
| Ox | 0.0001 | 0.1 | 0.0001 | ||||
| Oy | 0.0001 | 0.1 | 0.0001 | ||||
| Oz | 0.0001 | 0.1 | 0.0001 |
Табл. 4. Накопленная за 1367 секунд от разбега до набора высоты 11км ошибка алгоритма навигации при идеальной калибровке инерциального блока системы измерения.
| Ошибка навигации по координатам (Xобъект – Xнавиг) Вариант моделирования | X, м | H, м (без учета баровысотомера) | H, м (с учетом баровысотомера) | Z, м | Ψ, гр. | θ, гр. | γ, гр. | α, гр. | β, гр. | Vxg, м/с | Vyg, м/с | Vzg, м/с | |
| Без учета вращения Земли | Шаг измерения 3мс | 181.4 | -9.56 | 0.091 | 139.7 | 1.4e-3 | 1.46e-3 | 7.35e-4 | 9.04e-3 | 0.064 | 1.0e-3 | -0.043 | 0.216 |
| Шаг измерения 1мс | 170.3 | 7.204 | 0.025 | 96.95 | -2.2e-3 | 4.5e-4 | -1.8e-4 | 1.33e-4 | 0.036 | 0.08 | -5.2e-4 | 0.123 | |
| С учетом вращения Земли | Шаг измерения 3мс | 102.0 | 18.04 | 0.564 | 820.7 | 0.012 | 1.9e-3 | -8.9e-3 | 9.6e-5 | 0.188 | -0.15 | -0.012 | 0.648 |
| Шаг измерения 1мс | 89.38 | 13.28 | 0.452 | 116.6 | -6.4e-4 | 1.49e-3 | 6.6e-5 | -4.7e-3 | 0.034 | -0.09 | 0.016 | 0.125 |
Табл. 5. Накопленная за 1367 секунд от разбега до набора высоты 11км ошибка алгоритма навигации по параметрам калибровки (с шагом измерения 3мс).
| Ошибка навигации по координатам (Xобъект – Xнавиг) Вариант калибровки | X, м | H, м (без учета баровысотомера) | H, м (с учетом баровысотомера) | Z, м | Ψ, град. | θ, град. | γ, град. | α, град. | β, град. | Vxg, м/с | Vyg, м/с | Vzg, м/с | ||
| Идеальная калибровка | 102.0 | 18.04 | 0.564 | 820.7 | 0.012 | 1.9e-3 | -8.9e-3 | 9.6e-5 | 0.19 | -0.149 | -0.012 | 0.65 | ||
| Неточная калибровка по отдельно выбранному ниже указанному параметру (на k%) | ||||||||||||||
| Д Л У | Смещение нуля | 1% | 91.07 | -67.35 | -1.207 | 748.43 | 0.012 | 6.06e-4 | -7.6e-3 | 0.028 | 0.17 | -0.178 | -0.117 | 0.58 |
| 2% | -25.46 | 181.84 | -3.371 | 661.74 | 0.012 | 8.32e-3 | -6.68e-3 | 0.073 | 0.14 | -0.301 | -0.288 | 0.48 | ||
| Погрешность масштабного коэффициента | 1% | 74.33 | -815 | -16.72 | 762.37 | 0.012 | 1.7e-3 | -7.7e-3 | 0.342 | 0.19 | -0.145 | -1.244 | 0.67 | |
| 2% | 72.55 | -1503.2 | -31.907 | 720.96 | 0.011 | 2.06e-3 | -8.44e-3 | 0.628 | 0.208 | -0.095 | -2.274 | 0.72 | ||
| Неортогональность датчиков | 1% | 130.88 | 19.64 | 0.698 | 815.52 | 0.012 | 1.02e-3 | -4.3e-3 | 0.189 | -0.13 | 2.2e-3 | 0.65 | 0.13 | |
| 2% | 128.78 | 13.45 | 0.579 | 802.82 | 0.011 | 1.45e-3 | -7.66e-3 | -4.53e-3 | 0.18 | -0.128 | 4.9e-3 | 0.618 | ||
| Д У С | Постоянная составляющая смещения нуля | 1% | 318.33 | 27.77 | 0.837 | 676.9 | 6.0e-3 | -1.0e-3 | -0.011 | -5.5e-3 | 0.105 | 0.244 | 0.013 | 0.37 |
| 2% | 442.83 | 18.12 | -0.512 | 528.7 | 4.5e-4 | -2.79e-3 | -0.013 | 0.015 | 0.023 | 0.34 | -0.056 | 0.09 | ||
| Коэффициент линейной составляющей смещения нуля | 1% | 143.08 | 5.808 | -3426.5 | -0.267 | -0.181 | -0.171 | -0.14 | -3.67 | 15.03 | 0.405 | -11.5 | ||
| 2% | 9027.4 | 352.8 | 19.845 | -6735.0 | -0.509 | -0.348 | -0.318 | -0.476 | -7.225 | 27.66 | 1.44 | -21.8 | ||
| Погрешность масштабного коэффициента | 1% | -13.6 | 9.72 | 0.303 | 873.6 | 0.016 | 3.84e-3 | -6.6e-3 | 2.7e-3 | 0.23 | -0.398 | -0.021 | 0.77 | |
| 2% | -142.7 | 8.142 | 0.306 | 941.73 | 0.02 | 5.5e-3 | -5.0e-3 | 2.12e-3 | 0.267 | -0.646 | -0.022 | 0.906 | ||
| Неортогональность датчиков | 1% | 151.44 | 16.41 | 0.467 | 819.04 | 0.011 | 1.85e-3 | -8.6e-3 | -2.5e-3 | 0.18 | -0.1 | -7.6e-3 | 0.64 | |
| 2% | 148.58 | 12.88 | -0.322 | 824.86 | 0.012 | 1.45e-3 | -8.17e-3 | 0.017 | 0.187 | -0.104 | -0.073 | 0.642 | ||
| Неточная калибровка по всем вышеуказанным параметрам | 1% | 4782.5 | -176.7 | 4.84 | -3053.1 | -0.255 | -0.175 | -0.166 | -0.128 | -3.37 | 14.38 | 0.371 | 10.6 | |
| 2% | 7833.1 | -290.19 | 13.506 | -5577.5 | -0.465 | -0.325 | -0.298 | -0.356 | -6.263 | 25.131 | 1.014 | -18.9 |
Выводы
Приведенные результаты моделирования позволяют оценить роль точности калибровки по тому или иному параметру на точность навигации самолета.
Наличие полных моделей позволяет оценить роль всех параметров входящих в систему «Самолет – Среда – ИВК – САУ» (законы управления и их погрешности) на точность навигации самолета.
Оценки чувствительности компонент вектора ошибок навигации по погрешности калибровки позволяют формировать требования к рациональному распределению требований по точности калибровки для обеспечения заданной точности выдерживания компонент вектора состояния самолета.