Исходные данные
| № зада – ния | Производитель – Ность | DР *10 5 Па | Хс, % (масс) | W, % (масс) | rж кг/ м3 | rт, кг/ м3 |
m*10-3
Па 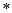 с с
|
m пр
*10-3
Па 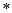 с с
|
Vпр 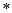 103
м3 / кг
103
м3 / кг
|
Rф.п. 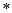 10-9,
1/ м
10-9,
1/ м
| ||||
| Vc, м3/ час | Gт, кг/час | |||||||||||||
| - | 432,0 | 6,0 | 8,5 | 1,30 | 1,27 | 1,2 | 39,0 | |||||||
№  Величины
Величины
| ||||||||||||||
| r0,.10-12, 1/ м2 | - | |||||||||||||
| rm.10-9 , м/ кг | ||||||||||||||
1  Расчет процесса и выбор аппарата
Расчет процесса и выбор аппарата
Фильтрование – это технологическая операция разделения неоднородных (гетерогенных) систем – суспензий или аэрозолей при помощи пористых (фильтровальных) перегородок, задерживающих твердую (дисперсную) фазу и пропускающих жидкую или газовую фазу (дисперсионную среду). Движущая сила процесса - разность давлений 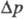 по обе стороны фильтровальной перегородки. Процессы фильтрования суспензий и дымов обычно рассматривают раздельно. В данной работе в дальнейшем речь пойдет лишь о фильтровании водных суспензий.
по обе стороны фильтровальной перегородки. Процессы фильтрования суспензий и дымов обычно рассматривают раздельно. В данной работе в дальнейшем речь пойдет лишь о фильтровании водных суспензий.
Методика расчета процессов фильтрования
Расчет процесса фильтрования включает следующие этапы:
· составление материального баланса и определение материальных потоков;
· определение необходимой поверхности фильтрования для обеспечения заданной производительности фильтра;
· вычисление объема промывной жидкости;
· определение продолжительности промывки осадка.
Методика расчета зависит от типа и конструктивных особенностей фильтра, характера заданных и определяемых величин и условий проведения процесса фильтрования.
Материальный баланс процесса фильтрования
|
|
Материальный баланс для процесса фильтрования составляют для определения производительности фильтровальной установки по осадку, фильтрату или исходной суспензии. Соответствующие уравнения имеют вид:
для всей гетерогенной системы
Gс = Gф + Gос, (1)
для твердой фазы
Gс.Хс= Gос.Хос, (2)
или
Gс.Хс = Gос(1 - W),
где W = (1 - Хос) – влажность осадка.
Решая уравнения (1) и (2), определяем составляющие материального
баланса.
Определяем массу суспензии:
т.к. Gт = Gс.Хс, то Gс = GТ/Хс
Gc = 432*100/8,5 = 5082,3кг/ч
Определяем массу жидкой фазы:
Gж = Gс - Gт
Gж = 5082,3 - 432 = 4650,3 кг/ч
Массовая концентрация в осадке равна
X ос = W – 1
Xос = 0,55 – 1 = 0,45 или 45%
Определяем массу влажного осадка:
т.к. Gс·Хс= Gос·Хос,
то 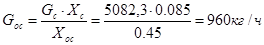
Определяем массу жидкой фазы во влажном осадке:
Gж (ос)= Gос - Gт = 960 – 432 = 528 кг/ч
Определяем массу фильтрата:
т.к. Gс = Gф + Gос
то Gф = Gс - Gос = 5082,3 – 960 = 4122 кг/ч
Результаты представляем в виде таблицы (табл. 1)
Таблица 1
Материальный баланс (кг/час)
| Приход, кг/час | Расход, кг/час | ||
| С суспензией | 5082,3 | С осадком | |
| В том числе: | В том числе: | ||
| Твердая фаза | Твердая фаза | ||
| Жидкая фаза | 4650,3 | Жидкая фаза | |
| С фильтратом | |||
| Всего | 5082,3 | Всего |
Материальный баланс сошелся.
Переход от весовых величин к объемным осуществляем с помощью плотностей соответствующих потоков (фаз). При этом плотность суспензии определяется в зависимости от способа выражения концентрации твердой фазы по уравнениям
|
|
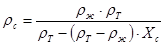 (3)
(3)
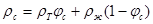 (4)
(4)
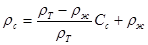 (5)
(5)
Аналогично определяют плотность влажного осадка, используя величины Хос, 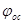 и Сос или понятие пористости слоя осадка
и Сос или понятие пористости слоя осадка 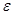 :
:
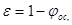 ,
,
откуда
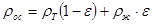 , (6)
, (6)
и влажности осадка W, тогда
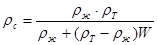 (7)
(7)
Вычисляем плотность суспензии и влажного осадка:
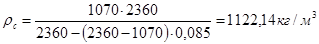
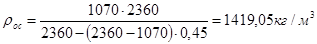
Уравнение фильтрования с образованием слоя осадка
Как показывает опыт, скорость фильтрования прямо пропорциональна движущей силе 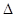 Р (разности давлений по обе стороны фильтровальной зоны) и обратно пропорциональна сопротивлению, возникающему в фильтровальной зоне (под фильтровальной зоной следует понимать фильтровальную перегородку со слоем образующегося на ней осадка). Скорость фильтрования можно определить как объем фильтрата Vф, проходящий через единицу поверхности S фильтровальной зоны за единицу времени
Р (разности давлений по обе стороны фильтровальной зоны) и обратно пропорциональна сопротивлению, возникающему в фильтровальной зоне (под фильтровальной зоной следует понимать фильтровальную перегородку со слоем образующегося на ней осадка). Скорость фильтрования можно определить как объем фильтрата Vф, проходящий через единицу поверхности S фильтровальной зоны за единицу времени 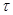 .Гидравлическое сопротивление фильтровальной зоны представляет сумму сопротивлений фильтровальной перегородки
.Гидравлическое сопротивление фильтровальной зоны представляет сумму сопротивлений фильтровальной перегородки 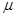 Rф.п. и слоя осадка
Rф.п. и слоя осадка 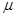 Rос.
Rос.
Сказанному соответствует дифференциальное уравнение скорости фильтрования:
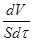 =
= 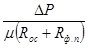 (8)
(8)
Сопротивление слоя осадка, очевидно, является функцией его толщины H, и для ламинарного режима течения фильтрата в фильтровальной зоне, что обычно и реализуется на практике, может быть представлено как
Rос = r0.H (9).
Коэффициент пропорциональности r0 (удельное объемное сопротивление осадка) имеет физический смысл величины гидравлического сопротивления равномерного слоя осадка толщиной 1 м.
Пренебрегая влиянием величины слоя осадка, образующегося за счет естественного (гравитационного) осаждения твердой фазы на рост толщины слоя осадка, можно принять, что его объем прямо пропорционален соответствующему объему фильтрата:
|
|
V ос = H.S = Х0.Vф,
откуда
H = Х0 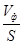 (10)
(10)
Коэффициент пропорциональности Х0 зависит от структуры осадка и от концентрации твердой фазы в суспензии
С учетом выражений (9) и (10) общее уравнение скорости фильтрования (8) можно представить в виде, более удобном для интегрирования:
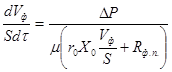 (11)
(11)
В практике проведения технологических расчетов процессов фильтрования наряду с объемным удельным сопротивлением осадка r0 пользуются также величиной среднего массового удельного сопротивления осадка rm. Эти величины связаны между собой соотношением:
r0 ·Х0 = rm ·Хm (12)
Здесь Хm = mт|./ Vф – масса твердой фазы осадка, образующегося при получении единицы объема фильтрата. Величины r0 и rm могут быть определены непосредственно из эксперимента или как функции движущей силы процесса фильтрования, а Х0, Хm – из выражений
Х 0 = 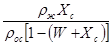 , (13)
, (13)
Х m = 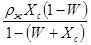 (14)
(14)
Величину Rф.п. в уравнении (11) можно считать постоянной (не зависящей от 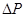 ) величиной, которая также определяется из эксперимента.
) величиной, которая также определяется из эксперимента.
Величины r0 , rm, Rф.п. , Х0, Хm называют также константами фильтрования.
Общее уравнение фильтрования (11) необходимо интегрировать по-разному в зависимости от следующих условий проведения процесса:
· фильтрование при постоянной движущей силе;
· фильтрование при постоянной скорости; 
· фильтрование при постоянных движущей силе и скорости;
· фильтрование при переменных движущей силе и скорости.
Поскольку в практике большинство фильтров работает в режиме постоянной движущей силы, а промывку можно рассматривать как фильтрование при постоянных движущей силе и скорости, представим результаты интегрирования основного уравнения фильтрования (11) для этих двух случаев.
Уравнение фильтрования при 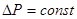
Vф2+ 2  Vф = 2
Vф = 2 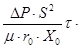 (15)
(15)
или
Vф2+2 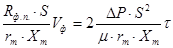 (16)
(16)