ГС, как и вертикальные, характеризуются гидродинамическим совершенством. Приток жидкости в реальную скважину отличается от притока в гидродинамически совершенную скважину тем, что в призабойной зоне пласта (ПЗП) и на забое скважины возникают дополнительные фильтрационные сопротивления, обусловленные с несовершенством вскрытия продуктивных пластов [4].
Для ГС выделяют два типа гидродинамического несовершенства скважин:
- по характеру вскрытия пласта, когда связь пласта со скважиной осуществляется не через открытый забой, а через перфорационные отверстия и каналы;
- по качеству вскрытия пласта, когда проницаемость ПЗП уменьшена по отношению к природной проницаемости пласта в результате техногенных воздействий (проникновение бурового раствора или его фильтрата, которые ухудшают фильтрационные параметры продуктивного пласта и т.д.)
При этом, следует отметить, что по степени вскрытия пласта ГС по отношению к вертикальным скважинам являются более гидродинамически совершенными.
Исследование притока жидкости к продольным по пласту (наклонным, горизонтальным скважинам) проводилось при ряде следующих упрощающих допущений:
1. Пласт бесконечный, горизонтальный, анизотропный, толщиной h, пористостью m, проницаемостью k в радиальном и kz в вертикальном направлениях, не зависящей от времени и давления.
2. Жидкость слабосжимаема, с постоянной вязкостью μ и коэффициентом сжимаемости βж.
3. Наклонная скважина длиной а эксплуатируется с постоянным, равномерно распределенным по этой длине дебитом q и имеет радиус rc. Угол наклона скважины, образуемый ее осью с нормалью к направлению простирания пласта, равен α. Скважина может быть заменена линейным источником, расположенным по ее оси.
|
|
4. Кровля и подошва пласта непроницаемы.
Для оценки количественных показателей используем прием, известный в гидродинамике и заключающийся в том, что формулы притока устанавливаются по зависимости неустановившейся фильтрации в бесконечном пласте, когда условие постоянного давления на контуре питания достигается введением фиктивной укрупненной нагнетательной скважины радиуса RK. Что касается прямолинейного контура питания, то формула притока непосредственно следует из метода отражения «источников – стоков» и вместо RK применяют удвоенное расстояние для прямолинейной границы.
Поступая таким образом, для несовершенной по степени вскрытия наклонной скважины получаем:
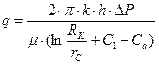, (2.1)
где: q – дебит несовершенной скважины, м3/сут;
k – коэффициент проницаемости пласта в зоне дренирования, м2;
h – эффективная нефтенасыщенная толщина пласта, м;
ΔР – разность давлений, под действием которой пластовая жидкость продвигается к забою скважины, Па;
μ – динамическая вязкость, Па·с;
RK – радиус контура питания скважины, м;
rc – радиус скважины по долоту, м;
С1 – коэффициент дополнительного фильтрационного сопротивления;
Са – «псевдо – скин» фактор, обусловленный наклоном скважины.
Коэффициент дополнительного фильтрационного сопротивления C1, обусловленный несовершенством ННС по степени вскрытия, можно определить по вертикальной ее проекции (аналогично ВС). Фильтрационное сопротивление несовершенной скважины, прилегающей к кровле анизотропного пласта, оценивается по формуле:
|
|
, (2.2)
где 
- модифицированная функция Бесселя первого рода нулевого порядка.
Вычисления позволили установить, что для несовершенной по степени вскрытия наклонной скважины (α ≤ 75º) формула для определения «псевдо – скин» фактора имеет вид:
, (2.3)
где b – вскрытая (по вертикали) толщина пласта;
- предельный угол отклонения скважины от вертикали.
Для определения притока (дебита) гидродинамически совершенной скважины справедлива формула:
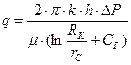, (2.4)
где СГ – коэффициент гидродинамического совершенства ГС.
В свою очередь данный коэффициент можно расписать для ориентировочных расчетов следующим образом (для изотропного пласта):
, (2.5)
где а – коэффициент равный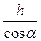 
;