Для выполнения программы теоретических исследований отводится два академических часа.
Объектом исследований, выполняемых в лабораторной работе, является линейная следящая система с запаздыванием, структурная схема которой приведена на рисунке 1.
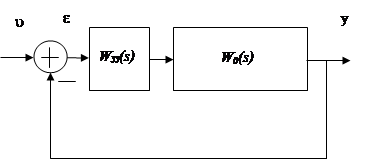 |
Рисунок 1 – Структурная схема исследуемой САУ с запаздыванием
На рисунке 1 WЗЗ(s)= e-ts – передаточная функция звена чистого запаздывания;
|
- передаточная функция предельной
разомкнутой САУ.
Программа теоретических исследований:
а) Изучить особенности процессов, протекающих в САУ с запаздыванием.
б) Изучить применение критерия Найквиста для анализа устойчивости систем с запаздыванием.
в) Определить с помощью передаточной функции предельной разомкнутой системы критическое время запаздывания.
Варианты значений параметров передаточной функции предельной разомкнутой САУ приведены в таблице 1.
Пункт в) теоретической части работы необходимо выполнить в форме предварительного отчета по лабораторной работе.
5. ПОРЯДОК ВЫПОЛНЕНИЯ ЭКСПЕРИМЕНТАЛЬНЫХ
ИССЛЕДОВАНИЙ
Для выполнения экспериментальных исследований и защиты лабораторной работы отводится четыре академических часа.
Программа экспериментальных исследований:
а) Построить переходные процессы в исследуемой САУ при изменении времени чистого запаздывания t от нуля до значений, при которых САУ станет неустойчивой. Определить критическое время запаздывания и сравнить его с рассчитанным теоретически. Провести анализ показателей качества при изменении t.
Переходные процессы можно построить, например, с помощью подсистемы Simulink пакета MATLAB. Для этого командой MATLAB File/New/Model необходимо создать новый файл модели, после чего в окне модели сформировать схему модели (рисунок 2). Для формирования модели использовать следующие элементы библиотек блоков Simulink:
- в библиотеке Continuous (аналоговые блоки) – блок передаточной функции Transfer Fcn (в параметре Numerator ввести коэффициенты полинома числителя передаточной функции предельной разомкнутой САУ в порядке убывания степени аргумента; в параметре Denominator ввести коэффициенты полинома знаменателя передаточной функции предельной разомкнутой САУ в порядке убывания степени аргумента).
- в библиотеке Sources (источники сигнала) – блок источника постоянного сигнала Constant, которым задается входное воздействие, соответствующее единичному скачку (параметр Constant value задается равным единице).
- в библиотеке Sinks – осциллограф Scope для построения графиков переходных процессов.
- в библиотеке Math – блок сумматора Sum (в настройке List of signs второй знак “+“ изменить на “-”).
- в библиотеке Continuous (аналоговые блоки) – блок Transport Delay, реализующий звено чистого запаздывания (в настройке Time delay задать значение времени запаздывания t, в настройке Initial input – ноль, настройки Initial buffer и Pade order оставить без изменения).
При необходимости файл модели сохраняется.
Перед построением переходного процесса необходимо предварительно задать параметры расчета посредством меню Simulation/ Simulation parameters окна модели. Для этого в пункте меню Solver (расчет) в разделе Simulation time (время моделирования) задается начальное (Start time) и конечное (Stop time) значение времени расчета. Начальное время задается равным нулю, а конечное время выбирается, исходя из условий решаемой задачи. Запуск задачи на выполнение осуществляется пунктом меню Start.
 |
Рисунок 3 – Схема исследуемой САУ c запаздыванием в окне модели Simulink
б) Построить годографы Найквиста исследуемой САУ при изменении времени чистого запаздывания t от нуля до значений, при которых САУ станет неустойчивой. Определить критическое время запаздывания и сравнить его с рассчитанным теоретически.
Годографы Найквиста можно построить, например, с помощью пакета прикладных программ Control System Toolbox – коллекции алгоритмов MATLAB для моделирования, анализа и проектирования САУ. Для этого с помощью команды меню File/New/M-file можно создать Script-файл следующего содержания:
clc;
sys= tf([1 1], [1 3 5 1])
sys.inputd=2
nyquist(sys)
В приведенном тексте вторая строка задает значения коэффициентов полиномов числителя и знаменателя передаточной функции предельной разомкнутой САУ; третья строка задает значение времени чистого запаздывания (в рассматриваемом примере оно равно двум); команда в четвертой строке производит построение годографа Найквиста.
Полученный М-файл сохраняется, а затем запускается на выполнение командой меню Debug/Run.
Переходные процессы и частотные годографы Найквиста исследуемой САУ с запаздыванием, построенные на экране монитора, распечатываются или зарисовываются и включаются в отчет по лабораторной работе.
6. СОДЕРЖАНИЕ ОТЧЕТА О ВЫПОЛНЕНИИ ЛАБОРАТОРНОЙ
РАБОТЫ
Отчет должен содержать:
а) Аналитическое исследование системы.
б) Кривые переходных процессов и частотных годографов Найквиста.
в) Развернутые комментарии к полученным графикам.
г) Краткие выводы.
Отчет по лабораторной работе должен быть выполнен в соответствии с требованиями ДСТУ.
Таблица 1 – Варианты индивидуальных заданий
| № вар. | Значения коэффициентов полиномов числителя и знаменателя передаточной функции предельной разомкнутой САУ | |||||
| b 1 | b 0 | a 3 | a 2 | a 1 | a0 | |
| 0.5 | ||||||
| 0.7 | ||||||
| 0.1 | 0.5 | |||||
| 0.3 | ||||||
| 0.4 | ||||||
| 0.7 | ||||||
| 0.6 | ||||||
| 0.7 | 0.7 | |||||
| 0.5 | ||||||
| 0.9 | 0.3 | |||||
| 0.1 | ||||||
| 0.2 | ||||||
| 0.8 | 0.8 | |||||
| 0.6 | ||||||
| 0.4 | ||||||
| 0.7 | 0.5 | |||||
| 0.5 | 0.3 | |||||
| 0.2 | 0.1 | |||||
| 0.8 | 0.6 | |||||
- КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что понимается в САУ под звеном чистого запаздывания?
2. Привести примеры САУ с запаздыванием.
3. В чем состоят характерные особенности процессов в САУ с запаздыванием?
4. Как влияет время запаздывания на устойчивость САУ?
5. Как влияет время запаздывания на качество САУ?
6. Как влияет время запаздывания на точность САУ?
7. Как определить критическое время запаздывания?