Уравнение звена с запаздыванием записывают в виде

СОДЕРЖАНИЕ

 

1. Цель работы 3

2. Краткие теоретические сведения 3

3. Описание технических средств выполнения работы 5

4. Порядок выполнения теоретических расчетов 5

5. Порядок выполнения экспериментальных исследований 6

6. Содержание отчета о выполнении лабораторной работы 7

7. Контрольные вопросы 7

Библиографический список 8

 

ЦЕЛЬ РАБОТЫ

 

Изучить влияние звена чистого запаздывания на устойчивость и динамические характеристики систем автоматического управления (САУ). Приобрести навыки применения критерия Найквиста к исследованию устойчивости систем с запаздыванием.

 

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Линейными системами с запаздыванием называются такие САУ, которые, имея в общем ту же самую структуру, что и обыкновен­ные линейные системы, отличаются от последних тем, что в одном или нескольких из своих звеньев имеют запаздывание во времени начала изменения выходной величины (после начала изменения входной) на величи­ну t, называемую временем чистого запаздывания, причем это время запаздывания остается постоянным и во всем последующем ходе процесса. Иными словами, у звеньев с чистым запаздыванием выходная величина повторяет все изменения входной величины с постоянным сдвигом по времени t, что в свою очередь приводит к сдвигу на t вправо выходной характеристики САУ.

Уравнение звена с запаздыванием записывают в виде

x_вых(t)= x_вх(t-t),

при этом входная величина x_вх(t) может быть любой функцией времени.

Теперь рассмотрим вопросы анализа устойчивости таких систем. Известно [1], что определение устойчивости САУ может производиться по корням характеристического уравнения. Характеристическое уравнение систем с запаздыванием - трансцендентно и имеет бесчисленное множество корней. Доказано [1, 2], что необходимым и достаточным условием устойчивости в данном слу­чае так же, как и в случае обыкновенной линейной системы, яв­ляется нахождение всех корней в левой полуплоскости. Алгебраи­ческие критерии устойчивости Рауса и Гурвица не могут быть непосредственно использованы для трансцендентных уравнений. Специальные критерии устойчивости для данных систем были разработаны Л.С.Понтрягиным, H.Г.Чеботаревым и Н.Н.Мейманом.

Однако для практического использования во многих случаях более удобным оказывается критерий Найквиста и другие частотные критерии устойчивости.

Идея применения частотных критериев для исследования устой­чивости систем с запаздыванием и распределенными параметрами высказывалась В.В.Солодовниковым и детально была разработана Я.3.Цыпкиным.

Пусть задана характеристическая функция

 

F(s) = D₀(s) + D₁(s)e^-st,

 

где D₀ (s) - полином степени n;

D₁ (s) - полином степени не больше п.

Рассмотрим функцию

 

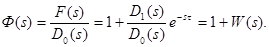(1)

 

Обозначим через N _Ф, N_F и N₀ число правых нулей функций Ф(s), F(s) и D₀(s) соответственно, а через Р_ф число правых полюсов функции Ф(s).

 

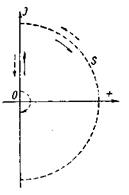
Рисунок 1 - Плоскость корней полиномов САУ

 

Будем обходить правую полуплоскость комплексной переменной в положительном направлении по контуру S, состоящему из дуги полукруга, имеющего бесконечно боль­шой радиус, диаметр на мнимой оси и центр в начале координат, и его диаметра (рисунок 1). Как видно из рисунка, при этом движение по мнимой оси будет сверху вниз (преры­вистая стрелка).

Пусть D₀(s) не имеет нуля в начале коор­динат, тогда функция W(s) не имеет полюса в начале координат. Естественно, у W (s) нет полюса и в бесконечности. Пусть D₀(s) не имеет также нулей на мнимой оси, т.е. годограф D₀(jw) не проходит через начало координат. Тогда можем применить принцип аргумента Коши для обхода по упомянутому контуру, так как на этом контуре нет по­люсов функции Ф(s).

Если s изменяется, оставаясь на рассматриваемом полукруге, то конец вектора Ф(s) в плоскости Ф также движется по замкнутому контуру, причем в соответствии с принципом аргумента число поворотов вектора в положительном направлении равно разности между числом нулей и полюсов функции Ф(s) внутри контура S, т.е. во всей правой полуплоскости:

 

DargФ(s)_S = 2p (N_ф - Р_ф).

 

Рассматривая (1), мы видим, что у функции Ф(s) число нулей N_Ф=N_F, а число полюсов Р_ф = N₀.

Условие устойчивости состоит в том, чтобы в правой полуплос­кости не было нулей функции F(s), т.е. чтобы N_F =0, и, кроме того, не было нулей функции F(s), лежащих на мнимой оси. Это означает, что

 

DargФ(s)_S = -2pN₀

 

и, кроме того, кривая F(jw) не должна проходить через начало координат.

При движении по дуге бесконечно большого радиуса функция D₁(s)/D₀(s) остается вещественной и постоянной, если степень D₁ равна степени D₀, и равна нулю, если степень D₁ ниже.

Пусть степень D₁ ниже степени D₀. Тогда W(s) _s=¥=0, и ар­гумент Ф(s) при движении по дуге S не изменяется, изменение его происходит только при движении по мнимой оси. Как мы от­мечали, это движение совершается сверху вниз, поэтому, чтобы судить об устойчивости по обычным частотным характеристикам, направление движения по которым определяется возрастанием частоты, мы переменим направление обхода (сплошная стрелка на рисунке 1), что приведет к изменению знака правой части:

 

 

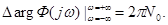(2)

 

 

Формула (2) обосновывает распространение на трансцен­дентные функции критерия Найквиста.

Пусть W(s) - передаточная функция разомкнутой системы, F(s) - характеристическая функция замкнутой системы, D₀(s) - характеристический полином разомкнутой системы.

Для того чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы вектор амплитудно-фазовой характеристики разомкнутой системы W(jw) при изменении w от нуля до беско­нечности повернулся бы N₀/2 раз в положительном направлении вокруг точки (-1, j0), (причем N₀ - число правых корней харак­теристического уравнения разомкнутой системы).

Из сказанного следует, что критерий Найквиста для систем, включающих звенья с чистым запаздыванием (или распределенными па­раметрами), оказывается совершенно таким же по форме, как и для обыкновенных линейных систем.

Полученные выводы можно обобщить на любые типы линейных систем с запаздыванием и распределенными параметрами. Не рас­сматривая этого вопроса до полного окончания, сделаем несколько наиболее важных обобщений. Например, если полином D₀(s) имеет нулевой корень, т. е. может быть представлен в виде D₀(s)= sD₀₀(s), то при движении по мнимой оси мы обойдем начало координат справа по дуге бесконечно малого радиуса и тем самым сможем сделать обобщение критерия Найквиста для астатических обыкновенных линейных систем.

Рассмотрим случай, когда передаточная функция разомкнутой системы имеет вид

 

W(s) = W₀(s)e^-ts, (3)

 

где W₀(s) — дробно-рациональная функция, имеющая r полюсов в правой полуплоскости. W₀(jw) называется амплитудно-фазовой характеристикой предельной системы. Как показано выше, ха­рактеристика W(jw) при изменении w от -¥ до +¥ должна r раз охватить точку (-1, j0).

Наиболее просто устойчивость исследуется в том случае, когда предельная разомкнутая система устойчива (или нейтрально ус­тойчива) и r =0. В этом случае достаточно рассмотреть картину пересечения характеристики предельной системы W₀(jw) и еди­ничного круга е^-jwt.

Как видно из (3), характеристика W(jw) получается ум­ножением W₀(jw) на е^-jwt, т.е. путем поворота каждого из век­торов W₀(jw) по часовой стрелке на угол wt.

Если разомкнутая предельная система устойчива и годограф W₀(jw) не пересекается с кругом единичного радиуса, т.е. рас­положена внутри него (рисунок 2а), то замкнутая система будет устойчивой при любом запаздывании, так как никакой поворот любого из векторов W₀(jw) не приведет к охвату точки (-1, j0).

Если имеет место одно пересечение (рисунок 2б), то при пово­роте вектора на угол y=w_кt_к характеристика попадет в точку (-1, j0), т.е. система будет находиться на границе устойчи­вости. Таким образом, система будет устойчивой, если выпол­няется неравенство

 

;

 

 

при нарушении неравенства, т.е. при t>t_к, устойчивость те­ряется. t_к получило название критического времени запаздывания.

 

 

 

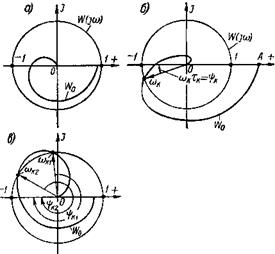
Рисунок 2 – Примеры частотных годографов систем с запаздыванием

 

При наличии двух пересечений (рисунок 2в) будем иметь ряд критических времен запаздывания:

причем по мере возрастания t система попеременно будет то устой­чивой, то неустойчивой.