Лабораторная работа № 2а
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПУАССОНА ВОЗДУХА
АКУСТИЧЕСКИМ МЕТОДОМ
КРАТКАЯ ТЕОРИЯ. При распространении акустической волны в газе каждый элемент объема среды, кроме колебательного движения, испытывает периодическую деформацию. В случае плоской волны эта деформация представляет собой совокупность объемной деформации (всестороннее сжатие и растяжение) и сдвиговой деформации. Сдвиговая деформация не сопровождается появлением упругих напряжений, проявляются лишь вязкие напряжения, что приводит к диссипации (рассеянию) энергии волны и к поглощению волны при распространении ее в среде. По представлениям Ньютона считалось, что объемная деформация среды в акустической волне представляет собой изотермический процесс. В этом случае величина скорости волны С (скорость звука) определялась бы изотермической сжимаемостью bt:
.
В дальнейшем согласно представлениям Лапласа стали считать, что деформация является адиабатным процессом, тогда скорость волны (скорость звука) определяется адиабатической сжимаемостью bад:
.
В этом случае в среде возникают области с различными температурами, так как в областях сжатия температура выше, чем в областях растяжения.
Однако поскольку газ обладает теплопроводностью, этот процесс не будет строго адиабатным. Причем этот эффект не будет влиять на величину скорости, приводя лишь к добавочному поглощению волны за счет теплопроводности.
Учет вязкости и теплопроводности среды позволяет говорить, что процессы деформации среды являются неравновесными процессами. Величина коэффициента поглощения характеризует неравновесность этих процессов.
Согласно теории распространения акустической волны (при учете рассматриваемых эффектов) скорость волны определяется соотношением:
, (1)
где r – равновесная плотность среды, bад – равновесная адиабатическая сжимаемость.
Коэффициент поглощения волны:
, (2)
где w - циклическая частота колебаний в волне, h - вязкость среды, c - теплопроводность среды, Суд V, Суд р – удельные теплоемкости среды при постоянном объеме и постоянном давлении соответственно.
Соотношение (1) носит название формулы Лапласа, соотношение (2) – формулы Стокса- Кирхгофа.
Для определения связи коэффициента Пуассона g со скоростью звука С рассчитаем равновесную адиабатическую сжимаемость bад. Воздух при атмосферном давлении будет считать идеальном газом, тогда согласно уравнению состояния Клапейрона-Менделеева:
. (3)
Уравнение адиабатного процесса для идеального газа имеет вид:
. (4)
Адиабатическая сжимаемость равна:
. (5)
Из (4) определим 
, для чего прологарифмируем (4), а затем возьмем дифференциал от левой и правой частей полученного соотношения:
(6)
Þ 
. (7)
Откуда:
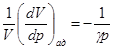и 
. (8)
Подставляя полученное выражение для bад в (1) получим:
. (9)
Подставив уравнение состояния (3), получим:
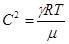. (10)
Соотношение (10) дает возможность определить показатель Пуассона, зная скорость звука:
. (11)
Определение g по скорости звука является достаточно точным методом. В соответствии с (11) относительная погрешность измерений показателя Пуассона g равна:
. (12)
Пренебрегая Dm/m и DR/R, получим:
. (13)
Современные методы измерения дают относительные погрешности DС/С »0,01% и DТ/Т »0,01%, поэтому относительная погрешность измерения показателя Пуассона Dg/g»0,03%.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА для определения скорости акустической волны представляет собой инперферометер с излучающим и приемным пьезопреобразователями.
Высокочастотное электрическое напряжение от генератора подается на излучающий пьезопреобразователь, который, благодаря пьезоэффекту, совершает механические колебания, излучая механическую волну в воздух в направлении второго преобразователя. Приемный преобразователь под действием волны так же начинает колебаться (деформироваться), на нем возникает переменное высокочастотное электрическое напряжение.
Напряжение приемного пьезопреобразователя подается на усилитель осциллографа. В этом случае на его экране наблюдается образование стоячей волны, в пространстве между пьезопреобразователями напряжение, поступающее на осциллограф, достигает максимального значения, что фиксируется визуально. При изменении расстояния между преобразователями на осциллографе наблюдается чередование максимумов и минимумов амплитуды сигнала. Изменение расстояния Х между преобразователями на DХ, равного половины длины акустической волны, соответствует расстоянию между соседними максимумами амплитуды волны. Для n промежутков между максимумами перемещение Хn+1 – Х1 равно:
. (14)
Откуда получим:
. (15)
Координаты первого (условно) Х1 и (n +1)-го Хn +1 максимумов отсчитываются по шкале микрометра.
Частота акустической волны измеряется частотометром, подключенным к генератору СВЧ.
Определив экспериментально длину волны l и частоту n, можно рассчитать скорость волны:
. (16)
В качестве пьезообразователей в установке использованы пьезокерамические преобразователи в виде дисков. Преобразователи идентичны и могут эффективно излучать (принимать) ультразвуковые волны на продольном резонансе (»400 кГц) и на радиальном резонансе (»190 кГц).
Примечание. Интерферометр обладает высокой чувствительностью к настройке на параллельность плоскостей преобразователей. Это требует специальной настройки юстировочными винтами.
ЗАДАНИЕ. Провести измерения длины акустической волны и определить скорость волны на двух частотах (продольного и радиального резонанса).