Задача №5
К концам невесомой нерастяжимой нити, перекинутой через невесомый неподвижный блок без трения в оси, подвешены грузы с массами m1= 1кг и m2= 2 кг. Каково ускорение, с которым движется второй груз?
Анализируем задачу.
Из условия невесомости и нерастяжимости нити следует, что сила натяжения нити на всех участках одинакова: T1 = T2 = T и система тел движется как единое целое с одинаковым по модулю ускорением:  .
.
Рассмотрим все силы, действующие на каждый груз отдельно: на I-ый груз действуют: m1g и T1,
на II-ой груз действуют: m2 g и T2. Систему отсчёта свяжем с Землёй.
Задачу решаем по алгоритму:
Дано:
m1 = 1 кг
m2 = 2 кг Решение:
 -? (м/с2 )
-? (м/с2 )
1. Изобразим рисунок и расставим все силы действующие на тело. Ускорение тела направим
В сторону большего тела.

2. Запишем II закон Ньютона в векторной форме для каждого тела



3. Выберем координатные оси, ось ОУ направлена по направлению ускорения, на рисунке
изображаем ОУ1, ОУ2.
4. Проецируем векторные уравнения II закона Ньютона для I и II тела на координатные оси ОУ1 и
ОУ2, у  читывая, что T1 = T2 = T,
читывая, что T1 = T2 = T,  .
.
ОУ1 : T- m1g = m1 ∙  (1) ОУ2: m2 g – T = m2
(1) ОУ2: m2 g – T = m2  (11)
(11)
Складываем уравнения (1) и (11 ), получаем: T – m1 g + m2 g – T = m1  + m2
+ m2 
 =
=  Ответ: 3,3 м/с2
Ответ: 3,3 м/с2
З  адача № 6
адача № 6
. Брусок массой 2 кг скользит по горизонтальной поверхности под действием груза массой 0,5 кг, прикрепленного к концу нерастяжимой нити, перекинутой через неподвижный блок. Коэффициент трения бруска о поверхность 0,1. Найти ускорение движения тела и силу натяжения нити. Массами блока и нити, а также трением в блоке пренебречь.
Д  ано Решение:
ано Решение:
m1= 2 кг 1.Изобразим рисунок и расставим все силы, действующие на тела.
m2 = 0,5 кг Ускорение первого тела направим вправо, второго - вниз.
µ = 0,1


 -?, Т -? (H)
-?, Т -? (H)
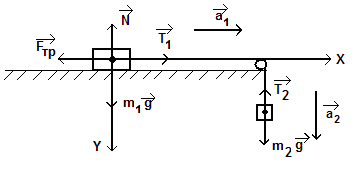
2. Запишем II закон Ньютона в векторной форме для каждого тела, поделив страницу пополам
для I тела: для II тела:





3. Спроецируем полученные уравнения на выбранные направления осей X и Y, учитывая условие невесомости и нерастяжимости: 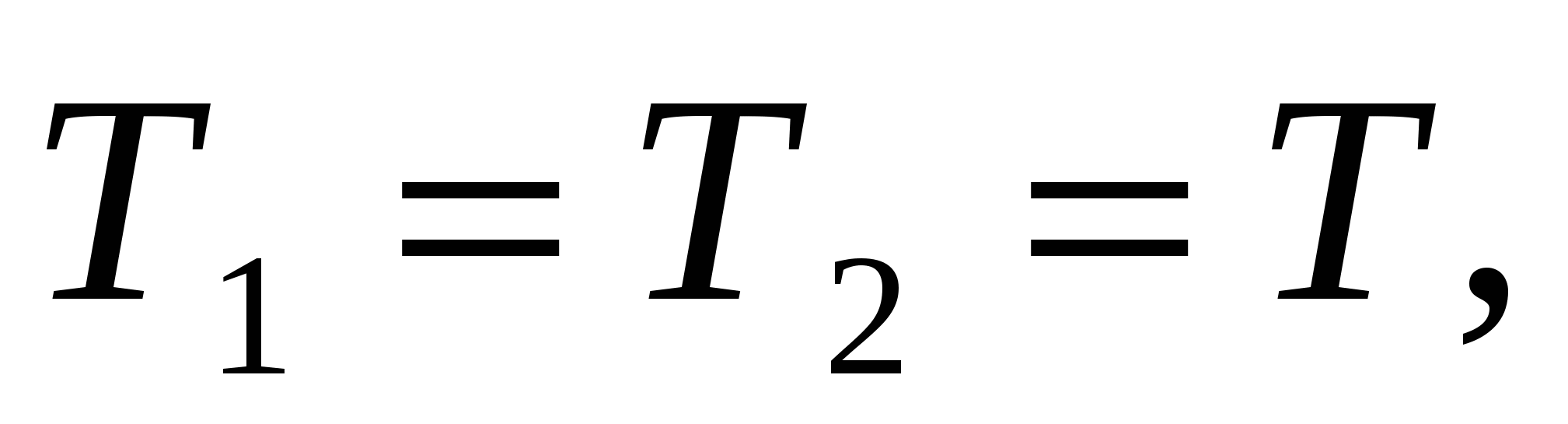
 .
.
 OX:
OX: 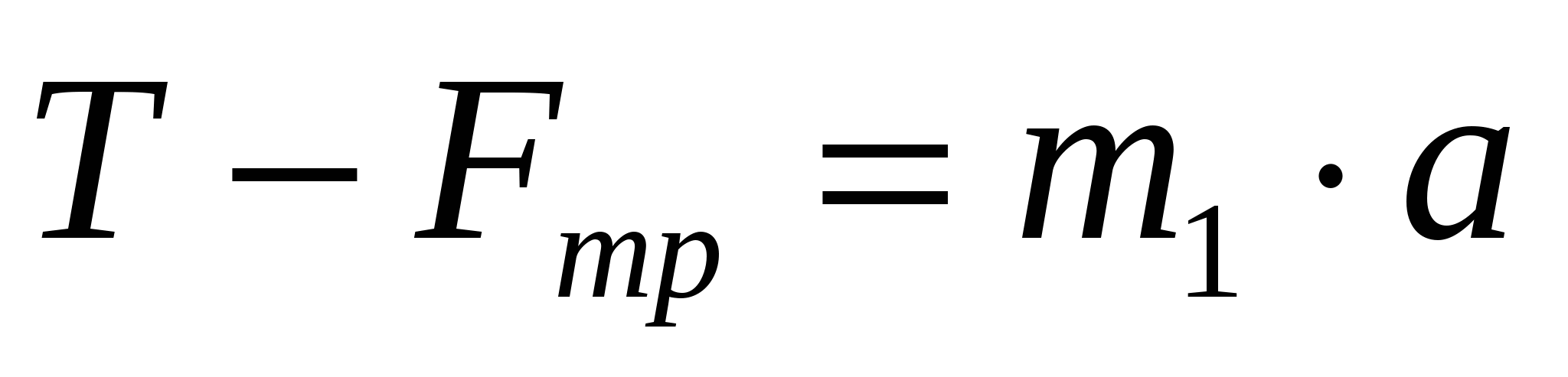 (1) OY:
(1) OY:  (31)
(31)
OY:  (2)
(2)
Из (2) следует, что N = m1∙ g, то Fтр= µ∙ N =µ ∙ m1∙ g.
Тогда уравнение (1) примет вид:  (3)
(3)
Решаем совместно систему уравнений (3) и (31) методом почленного сложения уравнений, получаем: Т - µ ∙ m1g + m2g – T = (m1+m2) ∙ 
откуда  ;
;  =
=  =
=  =
= 
Силу натяжения нити Т находим из уравнения (31): Т = m2g – m2  =m2 (g -
=m2 (g -  )
)
Т = 0,5 (10 – 1,2) = - 4,4 H. (знак «- » указывает, что сила натяжения направлена в противоположную сторону оси OY). Т = 4,4 Н.
Ответ: 1,2  ; 4,4 Н.
; 4,4 Н.
З  адача № 7
адача № 7
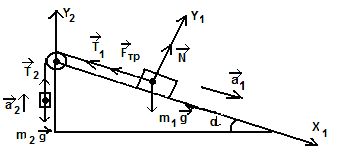
Груз массой 5 кг, связанный нерастяжимой нитью, перекинутой через неподвижный блок, с другим грузом массой 2 кг движется вниз по наклонной плоскости. Найти натяжение нити и ускорение грузов, если коэффициент трения между первым грузом и плоскостью 0,1, угол наклона плоскости к горизонту 450. Массами нитей и блока, а также трением в блоке пренебречь.
Дано: Решение:
m1 = 5 кг 1. Изобразим рисунок и расставим все силы.
m2 = 2 кг
µ = 0 α  = 450
= 450

 ; Т–? (Н)
; Т–? (Н)
2. Запишем II закон Ньютона в векторной форме.
для I тела для II тела


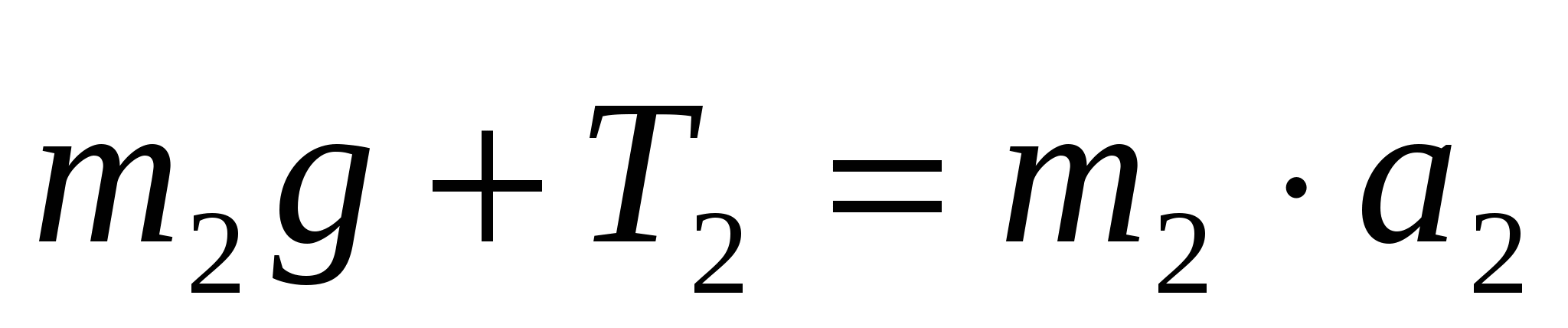
3. Спроецируем полученные уравнения на выбранные направления осей X1 , Y1 , Y2, учитывая условие невесомости и нерастяжимости: Т1 = Т2 = Т,  .
.
 OX1: m1g ∙ sin α – T- Fтр= m1∙
OX1: m1g ∙ sin α – T- Fтр= m1∙  (1) OY2: – m2 ∙ g +T = m2 ∙
(1) OY2: – m2 ∙ g +T = m2 ∙  (11)
(11)
OY1: N – m1∙g∙ cos α = 0 (2)
Из (2) уравнения находим, что N = m1 ∙g ∙ cos α,
поэтому Fтр = µ ∙ N = µ∙m1∙g∙cos α (3)
Подставляем (3) в (1), получаем:
m1∙g∙ sin α – T– µ ∙m1∙g∙cos α = m1∙  (4). Складываем почленно (11) и (4), получаем
(4). Складываем почленно (11) и (4), получаем
m1∙g∙sin α – T – µ∙m1∙g∙cos α – m2∙g + T=  (m1+m2)
(m1+m2)



Силу Т находим из уравнения (11): T = m2g + m2  = m2 (g+
= m2 (g+  ). T = 2∙ (10+1,7) = 23,4 Н.
). T = 2∙ (10+1,7) = 23,4 Н.
Ответ: 1,7  ; 23,4 Н.
; 23,4 Н.
IV. Подведение итогов урока.
.