Запишем уравнения II закона Ньютона в векторной форме для каждого тела

Ответ: 14,8 м/с

 

 

/

Задача 2. Тело массой 4 кг перемещается вверх по наклонной плоскости под действием связанного с ним невесомой и нерастяжимой нитью грузом массой 12 кг. Начальные скорости тела и груза равны нулю, коэффициент трения тела о плоскость равен 0,05, угол наклона плоскости равен 30^о. Определите ускорение, с которым движется тело, и силу натяжения нити. Считать, что блок невесом и трение в блоке отсутствует.

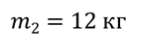
ДАНО:	РЕШЕНИЕ: Запишем второй закон Ньютона для тела и груза В проекциях на ось Ох: В проекциях на ось Оy: В проекциях на ось О’y’: 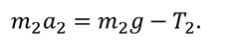Получаем систему уравнений 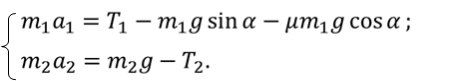Так как нить невесома и нерастяжима, а в блоке отсутствует трение, то: С учётом последних выражений преобразуем систему уравнений 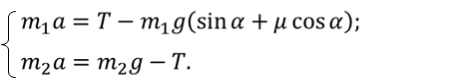Для того, чтобы решить эту систему уравнений сложим первое и второе уравнение. Тогда получим Преобразуем данное уравнение и выразим искомое ускорение Теперь определим силу натяжения нити

Ответ: 6,4 м/с²; 43,2 Н.

Задача 3. Два груза массами т ₁ = 5 кг и т ₂ = 2 кг связаны невесомой нерастяжимой нитью, переброшенной через невесомый блок, который прикреплен к вершине призмы, и могут скользить по граням этой призмы. Определите ускорение грузов, если начальные скорости грузов равны нулю, α = 60^о, β = 30^о, а коэффициент трения — 0,3.

ДАНО:

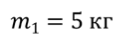
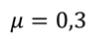
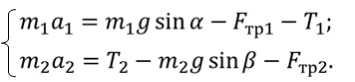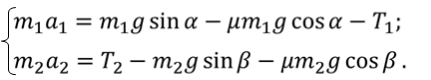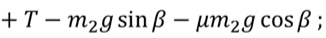
РЕШЕНИЕ: Запишем второй закон Ньютона для обоих грузов В проекциях на ось Оx и O’x’: В проекциях на ось Оy и О’у’: С учётом последних выражений преобразуем систему уравнений в проекциях на ось Оx и O’x’: Так как нить и блок невесомы: Так как нить нерастяжима и в блоке нет сил трения: С учётом последних равенств сложим первое и второе уравнение системы в проекциях на ось Оx и O’x’: Тогда искомое ускорение равно

О

Ответ:а= 2,6 м/с².

 

Задача 4. Трол­лей­бус мас­сой 12 т дви­жет­ся рав­но­мер­но под гору с укло­ном 0,05 рад при силе тяги 4 кН. Опре­де­лить силу со­про­тив­ле­ния дви­же­нию.

За­пи­сы­ва­ем крат­кое усло­вие за­да­чи и вы­пол­ня­ем по­яс­ня­ю­щий чер­теж:

 

 

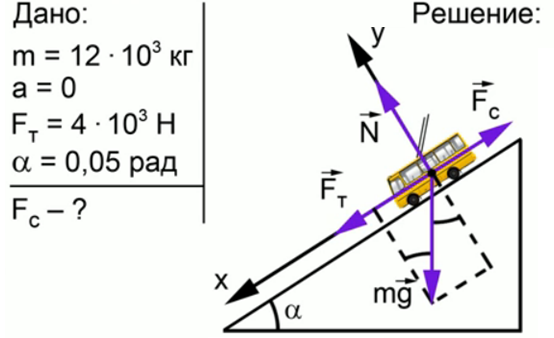
По ох: mg* sin a + F_т – F_c = 0 при а ≤ 0,1 рад а =sin a = tq a

Ответ: .

 

Тема №3 «Решение задач на движение связанных тел».

Цель: Диагностика знаний учащихся, необходимых для решения задач.

Физический диктант.

Тело движется горизонтально под действием силы F = 2H, масса тела 2кг, ч = 0.2.

Уравнение движения тела x = 3+2t-0,5t²

 

Задание

Зарисуйте все векторы.

Запишите II закон Ньютона в векторной форме.

Выберите оси координат и запишите закон в проекции на оси.

Найдите вес тела.

Найдите силу давления на поверхность.

Запишите уравнение зависимости V_x(t).

Найдите силу трения F_тр. (2 способа)

 

 

Ответы

1)

2) + _тр + m + = m 6) V_x= 2 – t²

3) F_тр-? F = ma N - mg =0 7) 1. F_m=чN N=mg F_m=чmg; F_m=0,2*2кг*10м/с²= 4Н;

4) P = N = mg P=20H 2. F_m= ma+ F; F_m= 1*2Н+ 2Н = 4Н

5) F_g = N = 20Н

.

 

Закрепление и расширение знаний, умений и навыков в решении задач.

Задача №1.

Два груза, массы которых m₁ = 0.1кг; m₂ = 0.2кг связаны нитью и лежат на гладкой горизонтальной поверхности. К левому грузу приложена F₂ = 0,5H; к правому F₁ = 3H. Чему равна сила натяжения нити?

Дано:

m₁ = 0.1кг

m₂ = 0.2кг

F₁ = 3H

F₂ = 0,5H

Найти

Т -?

 

Решение:

 

1. Изобразим все векторы сил действующие на тела.

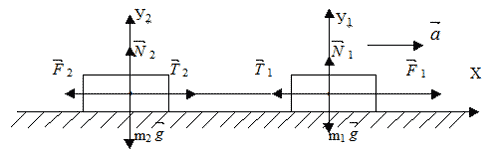
2. Запишем уравнение II закона в векторной форме для каждого тела.

I тело ₁ + ₁ + + m₁ = m₁

II тело + ₂+ ₂ + m₂ = m₂

Каковы значения Т₁и Т₂? Т₁ = Т₂ = Т

3. Запишем уравнение в проекциях на координатной оси.

ОХ: F₁ - Т = m₁a ОХ: Т - F₂ = m₂a

ОУ₁: N₁ - m₁g = 0 ОУ2: N₂ - m₂g = 0

4. Составляем систему:

F₁ - Т = m₁a

Т - F₂ = m₂a

F₁ - F₂ = a(m₁ + m₂)

a = в уравнение Т = F₂ +

5. сделайте вычисления, а так же выясните, изменится ли натяжение нити,если силы поменять местами.

Задача №2

Дано:

m = 1кг

m₁ = m

m₂ = m

m₃ = 2m

ч = 0,2

Найти

T₁ -? T₂ -?

Решение:

 

1. Изобразим все векторы сил действующие на тела.

Обратите внимание: нити две, соответственно силы натяжения разные Т₁ и Т_2.

2. Запишем уравнение II закона в векторной форме для каждого тела.

I тело: ₁ + m₁ = m₁

II тело: ₂ + + _тр + ₁ + m₂ = m₂

III тело: m₃ + ₂ = m₃

3. Запишем уравнение в проекциях на координатной оси.

0Y₁: T₁-m₁g = m₁a

0X: T₂ - T₁ - F_тр = m₂a m₃g - T₂ = m₃a

0Y₂: N - m₂g = 0 F_тр = чN=чm₂g

4. Составляем систему:

1) T₁-m₁g = m₁a

2) T₂ - T₁ - чm₂g = m₂a

3) m₃g - T₂ = m₃a

m₃g - m₁g - чm₂g = a(m₁+m₂+m₃)

g(2m-m-чm)=a(m+m+2m)

a = g(1-ч)/4

T₁=m₁(a+g) T₂=m₃(a+g)

Дорешайте в числах и найдите силу давления возникающую в оси левого блока (F_g=N) (Силу реакции действующую на ось левого блока)

Задача №3

На гладком столе лежит брусок массой 2кг, на котором лежит тело 1кг. Какую силу нужно приложить к нижнему бруску, чтобы он двигался с а = g/2? Коэффициент трения между брусками 0,5.

Дано:

M = 2кг

m = 1кг

ч = 0.5

а = 0.5 g

Найти РЕШЕНИЕ:

F -?

 

1. Изобразим все векторы сил действующие на тела.

 

Запишем уравнения II закона Ньютона в векторной форме для каждого тела

+ + _тр1+ m = m

+ + _тр2 + М + ₂ + = М

3. Запишем уравнение в проекциях на координатной оси.

0Х₁: Т - F_тр1 = mа

0X₂ : F - Т - F_тр2 = Ма

0Y₁ : N₁ - mg = 0

 

F_тр1 = F_тр2 =чmg

F_тр1 = ч N₁ = чmg

Так как F_тр1 = F_тр2, то уравнение для 2^го тела в проекции ось Y писать не обязательно!

4.Составляем систему:

Т - чmg = mа

F - Т - чmg = Ма

F - 2чmg = mа + Ма

F = а(m + М) + 2чmg =1/2 g(m + М) + mg

F = 1/2 g(m + М + 2m) =1/2 g(М + 3m) =1/2 ·10 · 2 = 25 Н..

Ответ: 25 Н

 

Задача № 4:

Два тела, связанные невесомой нерастяжимой нитью (см. рис.) тянут с силой 15 Н вправо по столу. Массы брусков m₁= 1 кг и m₂ = 4 кг, μ = 0,1.

С каким ускорением движутся бруски? Чему равна сила натяжения нити?

Ч

Сила натяжения нити на всех участках одинакова и все тела движутся с одним и тем же ускорением, т.е.

Т₁ = Т₂ = Т, .

Чтобы решить задачу, надо её проанализировать.

Рассмотрим все силы, действующие на каждое тело отдельно. Оба тела взаимодействуют с землёй, столом и нитью. На первое тело действуют: m₁g, Т₁, F_тр1, N₁. На второе тело действуют: m₂g, N₂, T₂,F_тр2 и сила F. Системы отсчета свяжем со столом.

 

Дано:

F= 15 Н

m₂ = 4 кг

m₁= 1кг

μ = 0,1_________

-? (м/с²); Т -? (Н) Решение

1. Изобразим все силы, действующие на тела. Ускорение тела направлено вправо.

Из условия задачи => Т₁ = Т₂ = Т; .

 

2. Запишем II-ой закон Ньютона в общем виде ∑ = m и для каждого тела в векторной форме, для этого страницу разделим пополам:

3. Выберем координатные оси: ось ОУ направим по направлению ,

а ось ОХ по направлению системы тел.

4. Проецируем векторные уравнения II закона Ньютона для I-го и II-го тела на координатные оси:

O X: T – F_тр1 = m₁ (1) OX: F – T – F_тр2 = m₂ ∙ (1^/)

OУ₁: N₁– m₁g = 0 (2) ОУ₂: N₂ – m₂g = 0 (2^/)

Поскольку из уравнения 2 => что Аналогично:

N₂ = m₂ ∙ g; то F_тр2 = μ · N₂ = μ ∙ m · g

N₁ = m₁g; то F_тр1= μ · N₁ = μ ∙ m₁g, тогда уравнение (1^/) II- го тела примет вид

тогда ур-ние (1) примет видF – T – μ ∙ m₂ ∙ g = m₂ (3¹)

Т – μ · m₁g = m₁ (3)

Получили два уравнения для 2-х тел, где учтены все силы, действующие на тела в отдельности.

Решаем совместно систему уравнений (3) и (3¹) методом почленного сложения уравнений, получаем: T – μ m₁g + F – T – μ m₂g = m₁

F – μg (m₁+ m₂) = (m₁+ m₂) (4), в этом уравнении учтены все силы, действующие на систему 2-х тел, связанных невесомой нерастяжимой нитью.

Откуда =

Силу натяжения нити находим из уравнения (3) или (3¹)

Т= μ ∙ m₁ · g + m₁ = m₁ (μ · g + ) = 1 (0,1 · 10 + 2) = 3Н

или Т = F – m₂ – μ · m₂ g = F – m₂ ( + μ ∙ g) = 15 - 4∙ (2 + 0,1· 10) = 3Н

Ответ: 2 м/с², 3Н