ФОРМИРОВАНИЕ ГЕОМЕТРИЧЕСКИХ ПРЕДСТАВЛЕНИЙ У СТАРШИХ ДОШКОЛЬНИКОВ
Автор работы: Марусина Наталия Викторовна
МДОУ «Детский сад №235» г. Саратов
Воспитательно-образовательная работа в дошкольных учреждениях строится с учетом закономерностей развития детей, требований дошкольной педагогики и дидактики. В соответствии с этими требованиями обучение детей опирается на непосредственное восприятие действительности, что особенно важно в дошкольном возрасте. Первоисточником знаний детей о действительности являются ощущения, чувственное восприятие предметов и явлений окружающего мира. Ощущения дают необходимый материал для формирования представлений и понятий. Характер этих представлений их точность и полнота зависят от степени развития у детей сенсорных процессов. Многообразный сенсорный опыт дошкольники получают в процессе обучения элементарной математики. Они сталкиваются с различными свойствами предметов (цвет, форма, величина), их пространственным расположением.
Форма является важным свойством окружающих предметов, она получила свое обобщенное отражение в геометрических фигурах. Другими словами, геометрические фигуры – это эталоны, при помощи которых можно определить форму предметов или их частей. /2/
Форма имеет большое значение при обнаружении, различении и узнавании предметов. Путем обследования, ощупывания, многократного обращения с предметом ребенок согласует свое восприятие с формирующимися у него представлениями о предмете. Он учится находить важные признаки предмета, сравнивать их с другими, по ним проводить группировку. Однако при обучении необходимо соблюдение принципа постепенного движения от конкретного к абстрактному, от эмпирического к научному, от чувственного понятия к логическому. Как видно, формирование представлений о форме занимает важное место в интеллектуальном развитии дошкольников. Таким образом, тема работы актуальна и нуждается в дальнейшем рассмотрении.
Предметом исследования опытной работы является процесс формирования элементарных математических представлений у дошкольников.
Объектом исследования нашей работы является формирование и развитие у дошкольников геометрических представлений.
Исходя из вышесказанного, можно обозначить цели и задачи работы:
1. Изучить и проанализировать научную и методическую литературу, которая содержит теоретические основы по данной теме.
2. Провести опытную работу в старшей группе детского сада с целью: сформировать у детей геометрические представления. Разработать и апробировать серию занятий, дидактических игр и упражнений, направленных на формирование геометрических представлений у детей; провести диагностику детей.
Формирование и развитие у дошкольников представлений о геометрических фигурах является одной из задач математической подготовки дошкольников. Вопросами развития у детей представлений о форме занимались многие методисты, педагоги, психологи, в частности А. М. Леушина, Л. А. Венгер, А. М. Пышкало, Д. Альтгауз и многие другие /1, 10, 12/. И не случайно, ведь формирование представлений о форме является важной задачей сенсорного развития ребенка, а именно с сенсорики, с восприятия предметов и явлений окружающего мира начинается умственное развитие ребенка.
Эталонами формы служат геометрические фигуры. Ознакомление с ними в рамках воспитания сенсорной культуры отличается от математических представлений. Усвоение эталонов формы предполагает знакомство с квадратом, прямоугольником, кругом, овалом, треугольником. Позднее может быть введена также форма трапеции. Однако во всех случаях имеется в виду умение узнавать ее и действовать с нею, а в математике же производится анализ фигуры, указывается количество и величина углов, сторон и т.д. Прямоугольник и квадрат, овал и круг даются детям как отдельные фигуры вне их соотношения, устанавливаемого геометрией, где, например, квадрат рассматривается в качестве частного случая прямоугольника. /4, с. 17./
Отметим, что знакомство детей с геометрическими фигурами следует рассматривать в двух направлениях: сенсорное восприятие форм геометрических фигур и развитие элементарных математических представлений, элементарного геометрического мышления.
Первое направление характерно для развития геометрических представлений у детей дошкольного возраста (3-5 лет), второе же направление – для детей постарше – 5-7 лет и для школьников.
Обучение детей обследованию формы предметов является непростым процессом. Прежде всего, возникает необходимость отделить геометрические фигуры от других предметов, придать им значение образцов. Это достигается тем, что каждую фигуру сравнивают с рядом предметов сходной с ней формы, предметы (или их изображения) группируются вокруг соответствующих фигур. Затем осуществляется переход к словесному обозначению формы предметов («крупный», «квадратный», «овальный»). Однако не многие предметы имеют простую форму, приближающуюся к той или иной геометрической фигуре.
В большинстве случаев форма предметов более сложна: в ней можно выделить общие очертания, форму основной части, форму и расположение более мелких частей, наконец, отдельные дополнительные детали.
При обследовании предмета детей приучают к соблюдению строгой последовательности осмотра по определенной схеме. На всех этапах обучения действиям по обследованию формы может использоваться прием обведения контура предмета и его частей. Он помогает сопоставлению обводимой формы с усвоенными эталонами. Уже в раннем детстве знакомые детям предметы опознаются независимо от их пространственного положения. Однако ребенок-дошкольник не узнает квадрата, если он находится перед ним не в привычном положении, а, например, повернутый на 45º. В таких случаях непосредственное сходство формы исчезает. Чтобы опознать квадрат, надо как бы мысленно повернуть его, что дошкольник сделать не может, так как его опыт практического действия с этим предметом весьма ограничен. Таким образом, «ребенок не видит еще тождественности формы различных предметов», которые мало ему знакомы, «поэтому не может обобщить их по признаку формы». /5, с. 94./
Исследования показывают, что вначале дети 3-4-х лет воспринимают геометрические фигуры как обычные игрушки и по аналогии с хорошо знакомыми бытовыми предметами, называя их именами этих предметов: цилиндр – стакан, столбик; трехгранная призма – крыша; конус – башенка; два лежащих рядом круга – очки и т.д. (С. Н. Шабалин).
Но под обучающим воздействием взрослых восприятие детьми геометрических фигур постепенно перестраивается. Дети уже не отождествляют их с предметами, а лишь сравнивают, отражая это в своей речи: цилиндр – как стакан, круг – как тарелка и т.д. И, наконец, геометрические фигуры начинают восприниматься детьми как эталоны, с которыми сравниваются жизненно-бытовые предметы (мячик, яблоко – это шар; морковь – это конус и др.)
Во многих работах психологов и педагогов /3, 8, 9/ доказано, что познание структуры предметов, их формы и размера осуществляется не только в процессе восприятия той или иной формы зрением, но и путем активного осязания, ощупывания ее под контролем зрения и называния словом. Совместная работа этих анализаторов способствует более точному восприятию формы предметов.
Однако зрительное восприятие предмета не удовлетворяет маленького ребенка. Чтобы лучше познать форму предмета и младшие и старшие дети стремятся коснуться его, взять в руки, потрогать, иногда повернуть, причем разглядывание и ощупывание различны в зависимости от формы и конструкции предмета. Поэтому весьма важную, а вернее, основную роль в восприятии предмета и определении его формы имеет обследование, осуществляемое зрительным и двигательно-осязательным анализаторами с последующим объяснением словом.
Но как отмечают многие авторы, Леушина А.М., Петерсон Л.Г. и др. /9, 10/, у детей дошкольного возраста наблюдается весьма низкий уровень обследования формы предметов: чаще всего они ограничиваются беглым зрительным восприятием и поэтому неточно определяют форму, не различают полностью форм овала и круга, прямоугольника и квадрата.
Кроме того, исследования показали /11, с. 56./, что самостоятельно дети не могут познать особенности предмета, вычленить его форму. Особенно в этом убеждает изобразительная деятельность детей.
Таким образом, в опознании формы рука и глаза взаимодействуют, помогая друг другу, а в слове фиксируется познаваемое.
Так, постепенно от характеристики первого направления перейдем к рассмотрению второго направления в развитии элементарного геометрического мышления детей.
В последнее время психологами и педагогами осуществлялась попытка более глубоко проникнуть в процесс развития геометрического мышления, раскрыть и выяснить его специфику. /10, с. 19./ С этой целью А. М. Пышкало определяет пять уровней мышления в области геометрии, которые условно называет «уровнями геометрического развития». /10/
Каждому уровню соответствует свой язык, содержащий определенную геометрическую и логическую терминологию, своя символика, своя глубина логической обработки изучаемого геометрического материала. Переход от одного уровня к другому не является процессом самопроизвольным, идущим одновременно с биологическим развитием человека и зависящим лишь от его возраста. Этот переход протекает под влиянием целенаправленного обучения, а потому зависит от содержания и методов обучения. Их изменение может содействовать ускорению перехода к следующему, более высокому уровню или тормозить этот переход. /10, с. 20./
Первый, исходный, уровень характеризуется тем, что геометрическая фигура рассматривается как «целое». На этом уровне при восприятии фигуры дети еще не выделяют ее элементом, не замечают, например, сходства между квадратом и прямоугольником. Фигуры различаются по своему внешнему виду. Ребенок, мыслящий на первом уровне, может легко научиться узнавать такие фигуры, как прямоугольник, квадрат, ромб и другие, хорошо запоминает их названия, но не видит общих признаков в этих фигурах.
При правильном обучении первый уровень может быть достигнут старшими дошкольниками и всеми учащимися 1 класса.
Дети, достигшие второго уровня, умеют устанавливать отношений между элементами фигур или самими фигурами. Они выполняют анализ воспринимаемых фигур. Усвоение свойств фигур происходит в процессе наблюдений, измерений, вычерчивания, моделирования. Эти свойства используют при узнавании фигур. Но свойства не выделяются и логически не упорядочены. Учащийся еще не понимает структуры логического следования. На этом уровне фигуры выступают носителями своих свойств и распознаются ими по этим свойствам.
Правильно организованное обучение, как показывают данные экспериментов, позволяет обеспечить достижение этого уровня всеми учащимися 3-го класса
Учащиеся, достигшие третьего уровня геометрического развития, уже умеют устанавливать связи между свойствами фигур и самими фигурами. На третьем уровне происходит логическое упорядочение свойств. Логические связи между свойствами устанавливаются с помощью определений. На этом уровне начинают понимать, что дедукция позволяет устанавливать свойства фигур более экономно и обще, чем с помощью эксперимента. На этом уровне квадрат считается прямоугольником, параллелограммом.
Обучение на третьем уровне геометрического развития в основном начинается в 4 классе и завершается к моменту окончания школы.
Четвертый уровень геометрического развития характеризуется тем, что учащиеся осознают значение дедукции в целом как способа построения всей геометрической теории.
Переходу на этот уровень способствует усвоение (понимание) роли и сущности аксиом, определений, теорем и др. Учащиеся на этом уровне четко видят различные возможности развития теории, исходя из различных посылок, и могут использовать дедуктивные построения не только в области изучения свойств одной какой-нибудь фигуры. Этот уровень вполне доступен учащимся 9-11 классов.
Пятый уровень мышления в области геометрии соответствует совершенному эталону строгости. На этом уровне достигается отвлечение от конкретной природы объектов и конкретного смысла отношений, связывающих эти объекты. Геометрия здесь приобретает общий характер и более широкие применения. /10, с. 22./
Переход одного уровня к другому, более высокому, осуществляется постепенно и последовательно. При этом элементы более высокого уровня зарождаются «внутри» предшествующего, появляются до того, как осуществлен переход к этому новому уровню. Причем и после перехода мы часто возвращаемся к более низкому уровню с целью лучше понять изучаемые на новом уровне вопросы. Все это дает возможность на каждом этапе обучения определить основной уровень, на котором ведется обучение, а также элементы, предшествующего и последующего уровней геометрического развития.
Итак, можно заметить, что развитие геометрического мышления – сложный процесс, куда включаются, по мнению И. С. Якиманской, «не только словесно-понятийные операции, но и множество перцептивных действий, без которых мыслительный процесс в форме образования протекать не может, а именно опознание объектов, представленных реально или изображенных различными графическими средствами». /17, с. 25./
Термин «геометрическое мышление» не является общепринятым, однако Якиманская И.С. пишет, что «всякое мышление есть обобщенное и опосредствованное отражение действительности в ее связях и отношениях», в том числе и геометрических. /17, с. 10./ Как известно, наиболее полно геометрические свойства и отношения, а также геометрические понятия исследуются и возникают в результате отвлечения от всех свойств и отношений объектов материального мира, кроме их взаимного расположения и величины. Так, понятие геометрического тела возникло как абстракция реального предмета, где сохраняется лишь форма и размеры при полном отвлечении от всех остальных свойств.
В дошкольном возрасте у детей складываются представления о геометрических фигурах, их характерных свойствах и признаках, а позднее, в школьном возрасте формируются уже понятия о геометрических телах.
Однако Пышкало А.М. отмечает еще одну особенность в формировании геометрических представлений детей. Это то, что «работа по изучению геометрического материала должна проводится как в естественнонаучной дисциплине», т.е. свойства фигур «выявляются экспериментально, усваивается необходимая терминология и навыки. Поэтому важное место в обучении должен занимать лабораторный метод. /10, с. 29./
Общаясь с разнообразными материальными моделями геометрических фигур, выполняя с этими моделями большое число опытов, дети выявляют наиболее общие их признаки, не зависящие от материала, цвета, положения и т.п.
Это достигается систематическим применением приема материализации изучаемых геометрических объектов… Отвлекаясь от конкретных свойств материальных вещей, учащиеся овладевают геометрическими представлениями.
Кроме того, Пышкало А.М. значительное место в методике отводит применению приема сопоставления и противопоставления геометрических фигур. /10, с. 31./ Это позволяет из множества фигур выделить множество кругов, множество прямоугольников, множество линий и т.д., а в дальнейшем это позволит уточнить свойства фигур, их классификацию. Большое внимание следует уделять противопоставлению и сопоставлению плоских (круг – многоугольник и др.) фигур, плоских и пространственных фигур (квадрат – куб, круг – шар). Эффективным, вызывающим качественные сдвиги в процессе формирования геометрических представлений является так же использование отношений взаимного положения фигур для установления их свойств.
Созданный запас геометрических представлений обеспечивает необходимую основу для проведения дальнейшей работы по формированию геометрических понятий.
При обучении детей геометрии применяются следующие средства. Это:
1. Использование разнообразных форм и методов организации учебной деятельности.
2. Создание атмосферы заинтересованности каждого ребенка.
3. Использование дидактического материала.
4. Стимулирование детей к высказываниям, использование различных способов выполнения заданий.
5. Поощрение стремления детей к самостоятельности.
6. Оценка деятельности ребенка не только по конечному результату, но и по процессу его достижения и др. /17, с. 105./
Отсюда видно, что целенаправленная деятельность воспитателя по формированию геометрических представлений создает благоприятные условия как для успешного усвоения курса математики в целом, так и для развития мыслительных процессов, самостоятельности.
Таким образом, можно отметить, что направления в развитии геометрических представлений у детей – различны. Ознакомление с геометрическими фигурами в плане сенсорной культуры отличается от их изучения при формировании начальных математических представлений. И тем не менее без чувственного восприятия формы невозможен переход к ее логическому осознанию.
Рассмотрим как происходит формирование геометрических представлений у детей дошкольного возраста в разных возрастных группах.
Ребенок, впрочем как и взрослый, использует геометрические фигуры, чтобы определить форму предметов и их частей. Знакомство младших дошкольников с геометрическими фигурами происходит в плане сенсорного восприятия формы этих фигур, что в дальнейшем позволит использовать их как эталоны в познании формы окружающих предметов. /1, с. 15./
Распознавание формы у детей начинается очень рано. К трем годам дети усваивают и некоторые названия форм: кругленький мяч, круглая тарелка и т.д., но еще не знают многообразных форм геометрических фигур: квадрата, круга, прямоугольника, которые воспринимаются как игрушки. Это, однако, не значит, что дети не различают их формы – они говорят: кубик и треугольник, чтобы строить дом и крышу; круг, квадрат, чтобы выкладывать красивый рисунок и т.д.
Предметы, окружающие детей, многообразны по своей форме, причем среди них значительно больше прямоугольных, чем округлых. Очень важно учить детей видеть форму предметов и элементарно группировать их на округлые и угольные. Основой этой группировки и должны служить известные детям геометрические фигуры. Уже сами дети говорят, что мяч, шар, тарелка – кругленькие, рыбка, огурец – круглые, но длинненькие, а кубик, книга, коробка – с углами. Поэтому дети 3-4 лет готовы к дифференциации предметов.
Детей II –ой младшей группы, то есть четвертого года жизни, учат различать и показывать круг, квадрат, треугольник. А различать, значит находить среди других. Знакомя с геометрическими фигурами, их предъявляют попарно. Ребенок находит у себя нужную фигуру, обводит ее рукой под руководством взрослого: «Смотри, как движется палец – прямо, потом угол, вниз, снова угол…». В самом конце воспитатель называет фигуру.
Вначале ребенок воспринимает каждую фигуру обособленно, не замечая сходства различия между фигурами. Поэтому на следующих занятиях круг и квадрат, находящиеся у воспитателя, будут отличаться от круга и квадрата у детей сначала по цвету, потом по величине, а затем и по цвету и по величине. Задание останется прежним: «Покажите то же, что у меня».
Таким образом, ребенок постепенно начинает абстрагировать форму от других признаков предмета. /2, с. 25./
Та же методика используется при знакомстве детей с треугольником, который сначала сравнивается с кругом.
Кроме того, в младшей группе детей знакомят с шаром и кубом. Проводят упражнения на сопоставление и группировку моделей этих фигур.
Для развития навыков обследования формы и накопления соответствующих представлений организуются игры для детей с досками, в вырезы которых вставляются модели плоских фигур. /14, с. 16./
В результате в конце учебного года дети второй младшей группы умеют находить среди разнообразных фигур круги, квадраты, треугольники, несмотря на то, что они могут быть представлены моделями разной окраски и размера.
В средней группе, с детьми пятого года жизни, продолжается работа по развитию представлений о форме, и работа эта осуществляется параллельно и органически увязывается с обучением счету, с упражнениями в сравнении величины предметов.
Большое значение имеет установление связи этой работы с обучением разным видам изобразительной деятельности, так как потребность воссоздать предмет (нарисовать, вылепить, сконструировать) вызывает необходимость четкого, расчлененного восприятия его формы. Основная задача, которая ставится перед детьми этой группы, состоит в том, чтобы познакомить детей с основными свойствами геометрических фигур.
Выделение несущественных свойств моделей наряду с их существенными признаками создает предпосылки для обобщения знаний о фигурах. Меняется цвет, размер, а признаки формы остаются постоянными. Ориентируясь на них, дети узнают фигуры.
С новыми геометрическими фигурами детей знакомят, сравнивая с уже знакомыми или друг с другом, сначала их сравнивают попарно, а затем сопоставляют группы фигур. Кроме того, важно формировать разнообразные действия детей с моделями фигур.
Действия с моделями, дети пробуют их катать, ставить в разные положения и выявляют их устойчивость или неустойчивость. Взаимное положение одной фигуры на другую – круга и квадрата, квадрата и прямоугольника, квадрата и треугольника – позволяет четче воспринять особенности фигур каждого вида, выделить их элементы. (12, с. 63.)
Кроме того, важное значение в средней группе придают обучению детей способам сравнения формы предметов с геометрическими образцами. У ребенка развивают умение видеть, какой геометрической фигуре или какому их сочетанию соответствует форма того или иного предмета.
Сначала дети упражняются в сопоставлении геометрических фигур с предметами сходной формы. Они подбирают предметы к моделям фигур. Так удается отделить модели геометрических фигур от других предметов, придать им значение образцов.
От непосредственного сравнения формы предметов с геометрическими образцами дети переходят к словесному определению формы предметов. Постоянно используются приемы осязательно-двигательного обследования предметов. Дети делают обобщение по признаку формы. Вне занятий проводятся игровые упражнения с целью развития умения зрительно расчленить изображения предметов на части и воссоздавать их из частей. /5, с. 213./
В старшей группе (шестилетние дети) основная задача воспитателя заключается в том, чтобы более глубоко познакомить детей с простейшими признаками и особенностями известных им геометрических фигур как эталонами для сравнения предметов по форме.
Дети шести лет не только хорошо различают, но и называют круг, квадрат, прямоугольник, треугольник, при этом знают, что все эти плоские фигуры могут быть разного размера и цвета. Знают они и объемные тела шар, куб, цилиндр. В старшей группе детей знакомят с фигурой овальной формы, формируется представление о четырехугольниках, а из объемных тел – знакомят с конусом и брусом. Все эти формы представлены в большом количестве предметов, окружающих детей, и целесообразно научить правильно именовать их.
В старшей группе каждая фигура представляется детям моделями разной окраски, разного размера и с разными соотношениями сторон, сделанными из разных материалов. Используются таблицы и карточки для индивидуальной работы, на которых рисунки фигур одного вида или разных видов расположены в разном пространственном положении. /15, с. 76./
Сопоставляя фигуры, детям необходимо предоставлять максимум инициативы и самостоятельности.
Для детей шестого года жизни существенное значение по-прежнему имеет использование приема осязательно-двигательного обследования моделей. Для выявления признаков отличия фигур друг от друга используется прием наложения и приложения. Дети считают элементы фигур, сравнивают количество сторон, углов моделей одного вида, но разного цвета или размера, а также количество сторон и углов квадрата и треугольника, прямоугольника и треугольника.
Для закрепления представления о фигурах наряду с приемами, которые применялись в средней группе, используются и новые. Так, дети делят фигуру на части различными способами, составляют целые фигуры из частей. Дети должны научиться не только последовательно выделять и описывать расположение фигур, но и находить узор по образцу и описанию. /11, с. 85./
Создаются предпосылки для развития аналитического восприятия формы предметов, состоящих из нескольких частей, чему способствуют дидактические игры и упражнения.
В подготовительной к школе группе знания у детей не столько расширяются, сколько закрепляются и систематизируются. При ознакомлении с геометрическими фигурами и закреплении представлений о них, используется те же методические приемы, что и в предыдущих группах.
Однако, следует отметить, что дети, занимающиеся по системе Л. В. Занкова, выполняют задания на поиск «спрятанных» фигур, выделяя и считая число вписанных в основную большую фигуру треугольников и прямоугольников. Это новый методический прием, используемый при обучении 6-7 летних детей. Сначала эти задания предельно просты, но постепенно становятся более сложными, так как количество вписанных фигур увеличивается, а их контуры все больше и больше пересекаются между собой. /16, с. 42./
Основная задача, которая ставится в этой группе перед детьми – систематизировать приобретенные знания, усвоить взаимосвязи между фигурами. Поэтому очень важно, чтобы дети познакомились с понятием многоугольника, являющимся обобщением понятий треугольника, квадрата, прямоугольника и др.
Дети должны не только различать, но и воспроизводить эти фигуры, зная их особенности и свойства.
При знакомстве с разными фигурами очень важно, чтобы у детей развивалась наблюдательность, чтобы они научились видеть особенности разных фигур, их свойства и различия; важно также подвести детей к вполне доступным им обобщениям, синтезу (например, хотя треугольники, как и четырехугольники, бывают разными, но треугольники, как и четырехугольники, являются одной из разновидностей многоугольников). /5, с. 316./
Для закрепления и уточнения знания о геометрических фигурах детям предлагаются разного рода задания на воспроизведение фигур.
В работе с детьми большую пользу приносят занимательные игры геометрического содержания, так как они развивают интерес к математическим знаниям, способствуют формированию умственных способностей. («Танграм», «Волшебный круг» и др.). (11) Но занимательные игры и задачи даются тогда, когда дети усвоили знания о форме и не только правильно называют ее, но и умеют воспроизводить, преобразовывать, видеть геометрическую основу окружающих предметов.
Таким образом, мы увидели, какие знания о геометрических фигурах получают дети за время пребывания в ДОУ. Помогают же в реализации задач математической подготовки, в том числе и в развитии геометрических представлений, образовательные программы, с помощью которых организуется воспитательно-образовательный процесс в дошкольных учреждениях.
В настоящее время в связи с совершенствованием воспитания и обучения детей осуществляется поиск новых методов, средств обучения, причем таких, которые способствовали бы выявлению потенциальных возможностей каждого ребенка. Одним из таких средств является занимательная математика, которая помогает подготовить детей к школьному обучению, в частности в области формирования геометрических представлений. По развивающему воздействию на детей можно выделить следующие основные виды задач:
1. Занимательные вопросы, задачи – шутки, способствующие развитию логического мышления, сообразительности, являющиеся приемом активизации умственной деятельности. Для решения задачи, ответа на вопрос требуется установление связей, отношений между объектами и явлениями.
2. Задачи – головоломки, цель которых – составить фигуры из указанного количества счетных палочек: 3 разных квадрата из 10; квадрат и 2 разных четырехугольника (прямоугольника) из 10 и д.р. В других аналогичных задачах осуществляется преобразование, видоизменение данной фигуры путем перекладывания или уменьшения количества палочек ее составляющих.
3. Группа игр на составление (моделирование) плоских и объемных изображений объектов. («Головоломка Пифагора», «Танграм», «Уголки», «Кубики для всех» и др.) Они способствуют развитию образного и логического мышления.
4. Очень разнообразны наглядные логические задачи: от самых простых, на заполнение пустых клеточек, продолжение ряда, поиск признаков отличия, до более сложных – нахождение закономерностей рядов фигур, признаков отличия одной группы фигур от другой. /2, с. 32./
В процессе решения этих задач у детей формируется умение сравнивать, обобщать, делать выводы. Так, для ответа на вопрос логической задачи: «Чем одна группа фигур (5-6 фигур треугольной формы с разным соотношением сторон, разного цвета, размера, расположения) отличается от другой (фигуры четырехугольной формы с теми же признаками сходства и отличия)?» необходимо проанализировать, сравнить фигуры, выделить общие признаки, свойственные всем фигурам одной и другой группы, а затем – признак отличия, указать правильность или ошибочность ответа.
Следует отметить, что уже в старших группах дети начинают понимать взаимосвязь между разными геометрическими формами, и если в младшей группе они находили среди окружающих предметов округлые или имеющие углы, то теперь их знания обогатились представлениями о многообразных геометрических фигурах, а эти представления систематизировались: дети узнали, что одни формы оказываются подчиненными другим, например, понятие четырехугольника обобщает такие понятия, как квадрат, прямоугольник, трапеция и другие, а понятие многоугольника обобщает все четырехугольники, все треугольники, пятиугольники и т.д., независимо от их размера и вида. Подобные взаимосвязи и обобщения, вполне доступные детям, поднимают их умственное развитие на новый уровень, готовит их к усвоению научных понятий в школе. /8/
Таким образом, математическую подготовку к школе следует рассматривать не только с точки зрения объема полученных детьми знаний, сколько с точки зрения их систематизации, то есть умственного развития детей и понимания ими значения математических знаний для жизни, формирование интереса к ним и стремления расширить их в дальнейшем.
Практическая работа по вопросам формирования представлений о геометрических фигурах проводилась в старшей группе детей 5-6-ти летнего возраста.
Дети к старшему дошкольному возрасту уже научились узнавать и называть такие геометрические фигуры как: круг, квадрат, треугольник, прямоугольник, а из объемных – шар, куб, цилиндр. В старшей группе закрепляются знания детей полученные ранее, а к тому же происходит знакомство с четырехугольниками, дети учатся узнавать в окружающих предметах формы знакомых геометрических фигур.
Прежде чем приступить к реализации этих программных задач с детьми на I этапе была проведена индивидуальная диагностика, которая позволила выявить имеющиеся у детей знания, умения и представления о геометрических фигурах. С детьми проводились собеседования, в ходе которых они выполняли задания и упражнения в игровой форме.
Первичная диагностика представлена диагностической картой № 1, диаграммой № 1, двумя таблицами с подробным описанием выполнения детьми заданий 1-3 (Приложение № 1).
Материализованный результат математической деятельности (по разделу «Геометрические фигуры») дал возможность тщательно проанализировать и выявить уровень усвоения детьми материала по данному разделу программы.
В ходе определения уровня сформированности геометрических представлений у детей, учитывались следующие показатели:
1. Различие и называние геометрических фигур, их признаков и свойств.
2. Уровень сформированности представлений о математических связях, отношениях, свойствах и закономерностях.
3. Владение терминологией и речевым выражением способов действия.
4. Использование знаний и умений для решения проблемно-игровых и практических задач.
В ходе собеседования детям предлагалось решить, а вернее выполнить три задания, а результаты их выполнения заносились в диагностическую карту (см.: «Диагностическая карта № 1»), а в конце проведенной диагностики была составлена диаграмма общего развития у дошкольников геометрических представлений.
В процессе решения задач каждым ребенком по всем показателям (показатели определены в описании задач и оценки каждого диагностического задания) определялись три уровня выполнения задания: низкий, средний, высокий.
Уровни определялись в зависимости от степени самостоятельности выполнения ребенком диагностического задания.
Полученные результаты заносились в Диагностическую таблицу № 1.
Результаты первичной диагностики можно проследить по диаграмме № 1
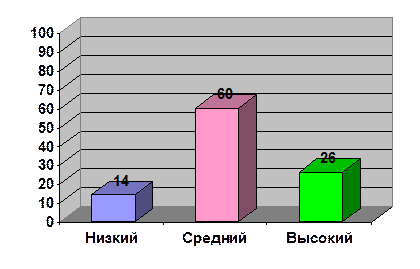
Данные диагностики показали следующие результаты:
14 % детей – низкий уровень знаний;
60 % детей – средний уровень знаний;
26 % детей – высокий уровень знаний.
Анализ проведенной диагностики с детьми старшей группы по формированию у них геометрических представлений показали, что в основном дети находятся на среднем уровне освоения программы по данному разделу математической подготовки дошкольников. Дети различают и называют геометрические фигуры, большинство детей узнают форму геометрических фигур в окружающих предметах, умеют выделять некоторые признаки геометрических форм.
Однако, как выяснилось, дети не могут применять знания и умения в решении проблемных и практических задач, у них не достаточно сформированы представления о математических, в частности, геометрических свойствах и закономерностях, у детей слабые навыки классификации.
Дошкольник, конечно, еще не может дать точного определения, что такое треугольник, квадрат и т.д., однако легко усваивает эти формы. А для того, чтобы ребенок не только говорил, что кубик не похож на шар, но и объяснял, чем именно отличаются эти две фигуры, необходимо вооружить его соответствующими словами (терминами), которыми дети владеют очень слабо и практически не применяют их в своей речевой деятельности, а ведь знание слов – терминов дали бы возможность детям рассказывать о существенных признаках геометрических фигур более полно и четко. /17, с. 32./
Отсюда возникают задачи, которые ставились при работе с детьми по формированию геометрических представлений с сентября по март месяц, в старшей группе:
1. Познакомить детей с четырехугольниками, учить узнавать и называть их.
2. Закрепить и расширить знания детей о геометрических фигурах, полученные в предыдущих группах.
3. С помощью дидактических игр (типа «Танграм» и др.) и упражнений уточнить и закрепить знания о свойствах, отличительных признаках и назначении геометрических фигур.
4. Провести индивидуальную работу с детьми, имеющими пробелы в знаниях по формированию геометрических представлений.
5. Провести промежуточную диагностику, с целью: выявить, как дети усваивают знания о геометрических фигурах, полученных на занятиях и в повседневной жизни.
6. В ходе проведения практической работы по развитию представлений о геометрических фигурах привлекать родителей к занятиям с детьми.
7. Развивать речевую активность детей, побуждая использовать в речи математические слова-термины; развивать навыки классификации, мыслительные процессы и операции.
Основной формой организации образовательного процесса в детском саду является образовательная деятельность - занятия, которым отводилось большое внимание в нашей работе. За время опытной работы с сентября