Основание 1 прибора (Общий вид изображен на рис. 2) оснащено регулируемыми ножками 2, которые позволяют горизонтально выравнивать прибор. В основании закреплена колонка 3, на которой закреплен верхний 4, нижний 5и средний 6 кронштейны. К среднему кронштейну прикреплено стреляющее устройство 7, а также прозрачный экран с нанесенными на него угловой шкалой 8 и фотоэлектрический датчик 9. Кронштейны 4 и 6 имеют зажимы, служащие для крепления стальной проволоки 13, на которой подвешен маятник, состоящий из двух мисочек, наполненных пластилином 10, двух перемещаемых грузов 11, двух стержней 12, водилки 14.
 |
Фотоэлектрический датчик соединен с привинченным к основанию универсальным секундомером 15 (FPM-14). На лицевой панели универсального миллисекундомера размещены следующие манипуляционные элементы:
«Сеть» -включатель сети. Нажатие этой клавиши вызывает включение питающего напряжения, которое определяют по свечению цифровых индикаторов (высвечивает цифру нуль) и лампочки фотоэлектрического датчика;
«Сброс» -сброс измерителя. Нажатие этой клавиши вызывает сброс схемы миллисекундомера FPM-14 и генерирование сигнала разрешение на измерение;
«Стоп» -окончание измерения. Нажатие этой клавиши вызывает генерирование сигнала разрешения на окончание процесса подсчета.
Порядок выполнения эксперимента
Определение скорости пули производится следующим способом:
1. Максимально приблизить грузы друг к другу.
2. Обнулить маятник, т.е. установить маятник в таком положении, чтобы черта на мисочке показывала угол наклона j=0 по шкале.
3. Выпустить пулю из стреляющего устройства (при помощи лаборанта).
4. Визуально измерить максимальный угол отклонения маятника j по шкале.
|
|
5. Включить и обнулить счетчик времени. Для этого последовательно нажать на кнопки «Сеть», «Сброс», «Стоп».
6. Вручную отклонить маятник на угол j, заблокировать измеритель времени и пустить маятник. Деблокировка производится нажатием на кнопку «Сброс».
7. Измерить время для 10 колебаний и вычислить период – Т.
8. Максимально отдалить друг от друга грузы Rmax и повторить действия по пунктам 2, 3. 4, 5, 6.
9. Измерить время для 10 колебаний и вычислить период – Т1.
10. Скорость пули вычислить по формуле (33).
11. Измерения повторить три раза. Данные измерения (в системе СИ) занести в табл.1. Таблица 1.
| № | R, м | DR | N | t, с | T, c | DT | j, град | Dj | R1 м | DR1 | N1 | t1, с | T1, с | DT1 | j1, град | Dj1 | u, м/с | Du |
Рассчитать относительную погрешность измерений по формуле
12. Результаты измерений представить в виде
u=<u>±<Du>,
где <Du> -среднее арифметическое значение абсолютной ошибки измерения скорости, <u> -среднее арифметическое значение скорости.
Контрольные вопросы
1. Дать определение момента импульса как векторной величины.
2. Сформулировать закон сохранения момента импульса.
3. Доказать тождественность формул момента импульса (L=mul и L= mu) для материальной точки.
|
|
4. Записать закона сохранения момента импульса для случая абсолютно - упругого удара пули.
5. Можно ли считать, что кинетическая энергия пули в случае неупругого удара полностью переходит в потенциальную энергию крутильного маятника?
ЛАБОРАТОЛРНАЯ РАБОТА № 9
Определение скорости волны в вертикальной струне
Цель работы: Исследование колебаний струны и количественная проверка формулы для собственных частот и скорости распространения колебаний в струне.
Приборы и принадлежности: Стойка с натянутой струной, динамометр, источник питания.
Теоретическое введение
Волной или волновым процессом называется процесс распространения колебаний в упругой среде за счет сил сцепления. Если одну из материальных точек среды вывести из положения равновесия, то посредством упругих сил она увлечет за собой соседнюю точку, которая увлечет следующую и т.д. Материальная точка, выведенная из положения равновесия, называется источником волн (вибратором). Геометрическое место точек, до которых одновременно дойдут колебания от источника волн, называется фронтом волны. Точки фронта волны будут совершать колебания в одной фазе. В зависимости от формы фронта различают волны плоские, сферические, цилиндрические и т.д.
Совокупность колеблющихся точек данной среды представляет собой волновое поле. Точки волнового поля совершают вынужденные колебания под воздействием вибратора. Необходимо различать два движения в волновом поле: 1) колебательное движение каждой точки; 2) вовлечение в колебательном движение новых точек среды (распространение волны).
|
|
Волны подразделяются на продольные и поперечные. Продольной волной называется такая волна, в которой точки среды совершают колебания в направлении распространения волны (луча волны). Поперечной волной называется волна, в которой колебания точек среды совершаются в направлении, перпендикулярном направлению распространения волны. Продольные волны возможны во всех средах (твердых, жидких, газообразных), а поперечные –только в твердых телах.
Если волны распространяется по оси х, а точки среды (струны) колеблются по оси у, то уравнения плоской волны выражается формулой
(1)
где А –амплитуда, равная максимальному смещению точки относительно равновесного состояния; w -круговая частота; n -линейная частота; l -длина волны, равная расстоянию, на которое распространяется волна за один период колебаний Т, равный времени одного полного колебания точки среды; u -фазовая скорость волны; х –расстояние, пройденное волной за время t; k –волновое число, показывающее число волн, укладывающихся на волну, равную двум единицам длины. Между указанными величинами существуют следующие соотношения:
(2)
В уравнении (1) (выражение в скобках) есть фазы волны.
Дифференциальная форма записи уравнения (1) называется волновым уравнением и имеет вид
. (3)
Интерференцией называется явление взаимного усиления или ослабления волн при наложении двух или нескольких когерентных волн. Когерентным называются волны, имеющие одинаковые частоты и постоянные разности фаз колебаний. Интерференция наблюдается, в частном случае, при наложении двух встречных волн с одинаковой амплитудой. Падающая на преграду волна и отраженная волна? интерферируя, создают стоячую волну. Например, уравнение бегущей по струне будет
у1=Аsin(wt-kx), (4)
а отраженной
у2=Аsin(wt+kx+ 
), (5)
В результате интерференции этих двух волн получится результирующая волна, уравнение которой выражается формулой, называемой уравнением стоячей волны
у=2Аsin(kx)cos (kut), (6)
где
Аст=2Аsin(kx) (7)
Является амплитудой стоячей волны и зависит от координаты х, но не от времени t.
Исследуем уравнение (7). Точки, в которых
sin (kx)=0, (8)
Являются узлами волны, так как в этих точках амплитуда колебаний превращается в нуль. Тогда
kx=2np, (9)
где n =0,1,2,…. k –волновое число, равное
. (10)
Из равенства (9) и (10) узнаем, что при координатах
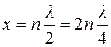(11)
образуются узлы.
Точки, амплитуды колебаний при которых максимальны, называются пучностями стоячей волны и удовлетворяют условию
sin (kx)= ±1, (12)
то есть kx= ±(2 n +1) p/ 2. Отсюда x= ±(2 n +1) p/ 4 соответствует координатами пучностей, так как в струне, закрепленной с обоих концов, образуется на концах узла Аст =0 sinkl= 0, где l –длина струны, а kl= 2 np. Отсюда
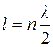, (13)
то есть для того, чтобы в струне образовалось стоячая волна, на длину струны укладывается целое число полуволн. Следовательно, зная длину струны и количество пучностей, можно найти длину волны, образованной в струне
. (14)
При n =1 образуется основной тон (рис.1, а), длина волны которого равна l =2 l.
При n =2 образуется первый обертон (рис. 1, б) с длиной волны l = l и т.д.
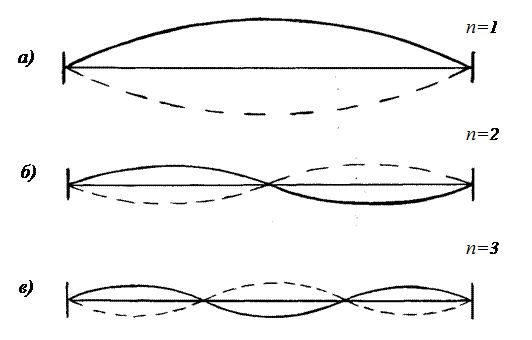При n =3 образуется второй обертон (рис. 1, в) с длиной волны l =2 l/3 и т.д.
Рис. 1. Колебания однородной струны с
закрепеленными концами
Круговая частота всех точек струны постоянна и равна
w=k × u, (15)
где u - скорость распространения импульса деформации вдоль струны, определяется по формуле
, (16)
с учетом того, что w=2pn.
Из равенств (15) и (16) с учетом (10) находим выражение для собственных частот струны
. (17)
При n =1 получим собственную частоту основного тона (рис. 1, а)
. (18)
Из уравнения (17) с учетом (14) и (16) получим формулу определяющей скорость волны
u=n × l (19)
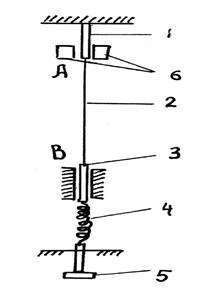Рис. 4. Cхема установки.
|
Описание установки
Схема экспериментальной установки приведена на рис.2. Струна 2 натянута между двумя точками А и В. Верхний конец струны А закреплен на короткий упругий элемент 1(полотно). Нижний конец струны В прикреплен к концу жесткого стержня 3, не участвующего в колебательном процессе, значит также закреплен неподвижно. Другой конец жесткого стержня 3 соединен с динамометром 4. Величина натяжения струны F определяется динамометром, а натяжение струны регулируется винтом 5. Ближе к верхнему
концу струны прикреплен электромагнит 6, который служит как вибратор (заставляет вибрировать упругий элемент). Электромагнит питается от сети через понижающий трансформатор.
Порядок выполнения работы
1. Включить шнур трансформатора в сеть.
2. С помощью винта регулировки натяжения струны добиться образования основного тона струны n =1, то есть одной пучности, и по формулам (14) и (18) определить частоту и длину волны основного тона струны, при этом r (линейной плотность струны) считать равным 5,74×10-4 кг/м, длину струны l =92 см.
3. Изменяя силу натяжения струны с помощью того же винта, можно добиться, чтобы струна давала устойчивую картину обертона, то есть получить 2,3,4 пучности.
4. Определить длину волн при n =2,3,4 по формуле (14).
5. Силу натяжения струны определить по шкале прибора.
6. Определить скорость распространения колебаний в струне по формулам (16) и (19) и сравнить результаты. При этом нетрудно убедиться, что волна в струне образуется в результате передачи импульса упругой деформации вдоль струны, так как скорость, определенная по формуле (16), равна скорости, определенной по формуле (19).
7. Все полученные результаты занести в таблицу:
| № п/п | n | n, c-1 | l, м | r, кг/м | l, м | F, Н | u, м/с | u, м/с | Du м/с | e отн.ед. |
| Ср. |
8. Построить график зависимости u=f(F).
9. Вычислить относительную ошибку
,
где DF –погрешность шкалы прибора (динамометра), а Dr -абсолютная погрешность определения плотности материала струны (Dr =0,005).
Контрольные вопросы
1. Как образуется механическая волна?
2. Что такое фронт волны?
3. Что такое волновое поле, и в каких двух движениях участвуют точки волнового поля?
4. Какая волна называется продольной и поперечной?
5. Что такое амплитуда, длина волны, период колебания, волновое число?
6. Что называется интерференцией волн?
7. Какие волны называют когерентными?
8. Когда возникает стоячая волна, и каким уравнением выражается?
9. Что называется узлами и пучности стоячей волны?
10.Напишите формулу, определяющие скорость волны в струне.
11. От чего зависит скорость стоячей волны в струне?
Список литературы
1. Детлаф А.А., Яворский В. М. Курс физики – М. Высшая школа, 1989 г.
2. Савельев И.В. Курс физики – М. Высшая школа, 1989 г. Т-1-2-3
3. Трофимова Т.И. Курс физики. М., "Высшая школа" 1997
4. Лабораторный практикум по физике /Под ред. А.С. Ахматова. –М.: Высшая школа, 1980.