К способам проведения экспертизы относятся: непосредственное измерение, ранжирование, сопоставление.
При непосредственных измерения экспертным методом значение физических величин или показателей качества определяются сразу в установленных единицах (единицах СИ, баллах, нормо-часах, и т. д.)
Такие измерения проводятся по шкале отношений, шкале интервалов или шкале порядка.
Непосредственно можно измерить весовые коэффициенты, измерение проводится по шкале интервалов.
Значение этих коэффициентов рассчитывается по формуле:


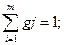
где n – количество экспертов,
m – число взвешиваемых показателей,
G i, j – коэффициент весомости, ранг;
j – го показателя в баллах, данный i – м экспертом.
Непосредственное измерение экспертным методом является сложным и предъявляет к экспертам высокие требования.
Ранжирование состоит в расстановки объектов измерения или показателей в порядке их предпочтения по важности или весомости. Место, занятое при такой расстановки, называется рангом. Чем выше ранг, тем предпочтительней объект.
По парное сопоставление – способ проведения экспертизы, когда измеряемые величины сравниваются между собой попарно и для каждой пары результаты сравнения выражаются в форме «больше - меньше» или «лучше - хуже». Затем измеряемые величины ранжируются (размещаются по рангам).
Примеры
Пример 1 Определить степень согласованности мнений пяти экспертов, результаты ранжирования семи объектов экспертизы приведены в таблице 1.
Таблица 1 – Результаты экспертизы для определения меры согласованности мнений экспертов
| Номер объекта экспертизы, j | Оценка эксперта, i | Сумма рангов | Отклонение от среднего арифметического | Квадрат отклонений от среднего арифметического | ||||
| 1-го | 2-го | 3-го | 4-го | 5-го | ||||
| -5 | ||||||||
| -13 | ||||||||

| 
|
Решение:
1) вычисляем среднее арифметическое рангов:

2) вычисляем сумму квадратов отклонений от среднего арифметического (S):
S = 630,
3)рассчитаем коэффициент конкордации (W):

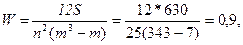
Ответ: Степень согласованности экспертов удовлетворительная.
Если степень согласованности мнений экспертов оказывается неудовлетворительной, принимают меры для ее повышения (тренировки, обсуждение результатов, разбор ошибок).
Пример 2. «Ранжирование». Результаты оценки 5 – ю экспертами 7 – ми объектов (по рангам) приведены в таблице 1.
По сумме рангов лучшим является седьмой объект, вторым по качеству – четвертый, затем – шестой, первый, второй, третий и пятый. Если же ранжирование проводиться с целью определения весовых коэффициентов gi для семи объектов, то они рассчитываются с использованием выше приведенной формулы:

Тогда весовые коэффициенты объектов имеют следующие значения:

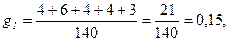
аналогично:




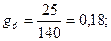

где 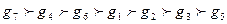

Пример 3 «Попарное сопоставление». В таблице 2 представлены результаты дегустации пищевых продуктов, обозначенных номерами от 1 до 6. Предпочтение i -го продукта над j -м соответствует 1, противоположному отношению – 0. Равноценности продуктов соответствует знак Х. Расставить продукты по качеству по шкале порядка.
Таблица 2 – Результаты экспертизы качества продуктов методом по парного сопоставления
| i - номер | j - номер | ||||||
| Итого | |||||||
| Х | |||||||
| Х | |||||||
| Х | |||||||
| Х | |||||||
| Х | |||||||
| Х |
Решение: Ранжированный ряд имеет следующий вид: №4; №5; №6; №2; №1; №3.
Пример 4 В таблице 3 представлены результаты попарного сопоставления мастерства певцов, выступивших на конкурсе вокалистов. Преимущество i – го солиста над j – м обозначено (1), j – го над i – м соответственно (-1), равноценные выступления обозначены (0). Определить итоги конкурса.
Таблица 3 - Результаты экспертизы мастерства певцов методом по парного сопоставления
| j - номер | |||||||
| i - номер | Итого | ||||||
| -1 | |||||||
| -1 | -1 | -1 | |||||
| -1 | -1 | -1 | |||||
| -1 | -1 | -1 | -1 | -1 | -5 | ||
| -1 | -1 | -1 |
Таблицы 2 и 3 являются избыточными. При попарном сопоставлении достаточно данных, по одну сторону от диагонали. Предпочтение при этом выражается указание номера предпочтительного объекта так, как это показано на таблице 4, переделанной из таблицы 2.
Решение: Победителем конкурса стал певец, выступавший третьем, второе место занял солист, выступавший первым. Третье, четвертое и пятое место поделили между собой вокалисты, выступавшие вторым, четвертым и шестым. Последнее место досталось певцу, выступавший пятым.
Таблица 4 – Результаты экспертизы методом по парного сопоставления
| Номер объекта экспертизы, j | Итого | ||||||
| Х | |||||||
| Х | |||||||
| Х | |||||||
| Х | |||||||
| Х | |||||||
| Х |
Решение: Ранжированный ряд имеет следующий вид: №4; №5; №6; №2; №1; №3.
Пример 5 Предположим, что в экспертизе 6 объектов участвуют 5 экспертов, причем все эксперты выразили свое мнение одинаково, т.е. мнение каждого из пяти экспертов представлено в таблице 4. Определить весомость каждого объекта и построить ранжированный ряд.
Решение:
Балл j – го объекта, определяемый i – м экспертом, рассчитывается по формуле:

где: Fi,j – частота предпочтения i - м экспертом j -го объекта,
С – общее число суждений одного эксперта,
m – число объектов экспертизы.

1. Определить частоты предпочтений каждым экспертом j – го объекта (Fi,j), т.е. сколько раз эксперт предпочел j – й объект пятью другим:






2. Рассчитаем общее число суждений каждого эксперта (С):

3. Рассчитаем балл или весомость каждого объекта экспертизы (Gi) по общему мнению, пяти экспертов:
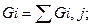


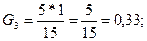



4. Определяем сумму баллов всех объектов экспертизы, по мнению пяти экспертов:

Поэтому, полученные в пункте 3 значения Gj рассматриваются, как нормированные и используются, как весовые коэффициенты.
5. На основании весовых коэффициентов записываем ранжированный ряд объектов экспертизы: (по мере убывания оценки)
№3 №1 №2 №6 №5 №4
Пример № 6.
В таблице 5 приведены мнения 4-х экспертов о 5-ти объектах экспертизы. Экспертиза объектов была проведена по одному показателю качества.
1. По сумме рангов каждого объекта экспертизы построить ранжированный ряд, являющийся результатом многократного измерения;
2. Определить весомость членов ранжированного ряда;
3. Определить степень согласованности мнений 4-х экспертов, вычислив коэффициент конкордации.
Таблица 5
| Мнение эксперта | Исходные данные |
| Мнение 1 эксперта | Q4 > Q3 > Q2 > Q5 > Q1 |
| Мнение 2 эксперта | Q1 <Q5 < Q2 < Q3 < Q4 |
| Мнение 3 эксперта | Q2 < Q1 < Q5 < Q3 < Q4 |
| Мнение 4 эксперта | Q4 > Q3 > Q5 > Q1 > Q2 |
Порядок расчета:
1. Заданные исходные данные надо представить в виде неравенств одного смысла. В рассматриваемом примере, мнение 3-го эксперта переписать в виде Q4 > Q3 > Q5 > Q1 > Q2, а мнение 4-го эксперта - в таком виде Q2 > Q1 > Q5 > Q3 > Q4.
2. Найдем сумму рангов каждого объекта экспертизы.
Таблица 6
| Номер объекта экспертизы | Оценка эксперта | Сумма рангов | Отклонение от среднего арифметического | Квадрат отклонения от среднего арифметического | |||
| 1-го | 2-го | 3-го | 4-го | ||||
| -1 | |||||||
| -1 | |||||||
|
3. Среднее арифметическое рангов:

4. Определим общее число суждений одного эксперта, связанное с числом объектов экспертизы «m»:
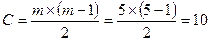
5. Вычислим весомость членов ранжированного ряда:

6. Вычислим коэффициент конкордации:

Вывод: при полученном коэффициенте конкордации (W = 0) степень согласованности мнений экспертов отсутствует.