Определение коэффициента поверхностного натяжения

ПО ВЫСОТЕ ПОДНЯТИЯ ЖИДКОСТИ В КАПИЛЛЯРНОЙ ТРУБКЕ.

Цель: изучить поверхностное натяжение жидкости, явление капиллярности,

исследовать зависимость высоты поднятия жидкости в капилляре от

величины коэффициента поверхностного натяжения.

Приборы и материалы: капиллярная трубка, два сосуда с исследуемыми

жидкостями, резиновая груша.

Теоретическое введение.

По своим свойствам и структуре жидкость занимает промежуточное положение между газами и твердыми телами.

С одной стороны, жидкость подобно газу не сохраняет формы, приобретая форму сосуда, характеризуется текучестью и вязкостью. При критических температуре и давлении граница между жидкостями и газами исчезает.

С другой стороны, по некоторым параметрам жидкости близки к твердым телам. Близки по значению их плотности, теплоемкости; их коэффициенты объемного сжатия одинакового порядка. Подобно твердым телам жидкостям характерна прочность на разрыв, могут пребывать в растянутом состоянии.

Этот двойственный характер связан с особенностью движения молекул жидкости. В твердом теле молекулы составляют кристаллическую решетку и колеблются около своего положения равновесия. В жидкостях среднее расстояние между молекулами больше, чем у кристаллов, и поэтому молекулы жидкости могут отходить от своих правильных положений.

Молекулы жидкости совершают колебания около временных положений равновесия. Побыв в таком положении некоторое время, молекула «перескакивает» в другое место и снова какое-то время живет в этом месте, совершая колебания, «оседлой жизнью». В «оседлом» состоянии молекулу жидкости удерживают упругие силы. Эти упругие силы обусловлены действием соседних молекул, расположенных на близком расстоянии.

Молекулярные силы очень быстро убывают с увеличением расстояния. При r~10^-9 межмолекулярное взаимодействие практически отсутствует (F→0). Это расстояние r называется радиусом молекулярного действия, а сфера радиуса r – сфера молекулярного действия.

Если по отношению к какой-то молекуле В (рис. 1), находящейся внутри жидкости, соседние молекулы расположены симметрично, то равнодействующая F всех сил, приложенных к молекуле В, равна нулю. Однако вследствие теплового движения равновесие нарушается, и молекула приходит в движение под влиянием равнодействующей силы F ≠ 0.

При сближении молекул друг с другом силы взаимного притяжения до определенного расстояния возрастают; при каком-то расстоянии между молекулами r=r₀ (r₀~2r_м, r_м≈10^{-8 м – радиус молекулы)} силы взаимодействия превращаются в ноль; если же расстояние между молекулами r<r₀, то вступают в действие силы отталкивания. В жидкости молекулы в основном находятся на расстоянии меньшем r₀, т.е. в жидкости преобладают силы отталкивания. Этим объясняется слабая сжимаемость жидкости.

Молекулы жидкости, расположенные на расстоянии от поверхности, меньше чем r, находятся в особом состоянии (молекулы А и С, рис. 1).

Действие на эти молекулы со стороны других молекул жидкости больше, чем со стороны молекул пара или воздуха. Поэтому равнодействующая сила всех действующих на такую молекулу молекулярных сил

рис.1 направлена внутрь жидкости, нормально к ее поверхности. Отсюда следует, что на все молекулы, расположенные в тонком поверхностном слое, действуют силы, стремящиеся втянуть их внутрь жидкости. Величина этих сил растет в направлении от внутренней к наружной границе слоя (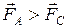). Благодаря этому поверхностный слой давит с большей силой на жидкость, создавая в ней так называемое внутреннее или молекулярное давление. Это давление очень велико (например, для воды ~11∙10⁸Н/м²).

Молекулы поверхностного слоя обладают избытком энергии сравнительно с молекулами, находящимися внутри жидкости. Эта избыточная энергия называется свободной поверхностной энергией или просто поверхностной энергией. Указанными свойствами поверхностного слоя обусловлено особое его состояние, которое подобно состоянию натянутой упругой пленки, стремящейся сократить свою поверхность до малых размеров. Стремление жидкости сократить свою поверхность называется поверхностным натяжением.

Силы поверхностного натяжения направлены по касательной к поверхности жидкости и действуют нормально к любой линии, проведенной на этой поверхности.

Для количественной характеристики силы поверхностного натяжения жидкости вводят коэффициент поверхностного натяжения α, который численно равен силе F, действующей на единицу длины произвольной линии ℓ, мысленно проведенной к поверхности жидкости:

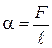(1)

При изотермическом увеличении площади поверхности жидкости совершенная работа равна свободной поверхностной энергии. Величина, численно равная работе изотермического увеличения площади поверхности жидкости на единицу, называется коэффициентом поверхностного натяжения:

(2)

В СИ единицы измерения: 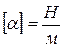или .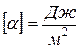

Коэффициент поверхностного натяжения различен для разных жидкостей. Он зависит от рода жидкости, от температуры (уменьшается с повышением температуры) и от степени чистоты поверхности (изменяется от малейшего загрязнения).

Растворение в жидкости различных веществ (поверхностно-активных веществ) изменяет величину коэффициента поверхностного натяжения.

Поверхностно-активные вещества (ПАВ) – органические вещества, различного химического строения, понижающие поверхностное натяжение на поверхности раздела фаз (жирные кислоты, их соли, спирты, эфиры и др.).

Эти вещества адсорбируются на поверхности раздела и уменьшают свободную поверхностную энергию. Повышенная концентрация (адсорбция) поверхностно-активных веществ в поверхностном слое объясняется тем, что перенос молекул этих веществ к поверхности требует меньшей затраты энергии, чем перенос молекул воды.

Если поверхность жидкости не плоская, а искривленная, то она оказывает на жидкость избыточное (добавочное) давление. Это давление обусловлено силами поверхностного натяжения.

В общем виде, когда поверхность жидкость является поверхностью двоякой кривизны, добавочное давление ∆ p поверхностной пленки определяют по формуле, которая была выведена французским ученым П.С. Лапласом в 1806г.:

, (3)

где α – коэффициент поверхностного натяжения, R ₁, R ₂ – радиусы кривизны любых взаимно перпендикулярных нормальных сечений поверхности жидкости.

Если поверхность сферическая, то R ₁ = R ₂, тогда формула Лапласа приобретает вид:

(4)

В узких стеклянных трубках с d ≤ 0,5 мм – капиллярах, опущенных в жидкость, хорошо заметно поднятие или опускание жидкости (рис. 2).

Возле стенок сосуда поверхность жидкости под действием молекулярных сил вследствие смачивания или несмачивания искривляется. Это явление объясняется различными значениями коэффициента поверхностного натяжения на границе: «жидкость - пар», «жидкость - твердое тело», «пар - твердое тело».

Поверхностная пленка жидкости в трубке жидкости и стекла принимает вогнутую или выпуклую формы (мениск). Если жидкость смачивает материал трубки, то внутри нее мениск имеет вогнутую форму (рис.2а), если не смачивает – выпуклую (рис.2б).

Под вогнутой поверхностью жидкости появляется избыточное отрицательное давление, определяемое по формуле (4). Наличие этого давления приводит к тому, что жидкость в капилляре поднимается. В случае явления несмачиваемости – жидкость в капилляре опускается. Капиллярность – явление изменения высоты уровня жидкости в

капиллярах.

Рис. 2 Жидкость поднимается или опускается в капилляре до тех пор, пока добавочное давление не станет равно гидростатическому давлению поднявшегося или опустившегося столба жидкости, т.е.

,

где ρ – плотность жидкости, h – высота ее понятия, g – ускорение силы тяжести,

α – коэффициент поверхностного натяжения, R – радиус кривизны поверхности.

Если r – радиус капилляра, q – краевой угол, то из рис. 2а следует, что

Откуда

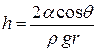(5)

Выражение (5) – формула Жюрена для высоты поднятия жидкости в капиллярах.

Для смачивающих жидкостей, в зависимости от их природы, угол q принимает значения в пределах 0 £ q £ p/2 и h > 0 (жидкость в капилляре поднимается). Для несмачивающих жидкостей краевой угол q принимает значения в пределах p/2 < q £ p и h < 0 (жидкость в капилляре опускается). Максимальное опускание или поднятие жидкостей будет наблюдаться в случае полного несмачивания (q = p) или полного смачивания (q = 0) капилляра. Для полного смачивания высота поднятия жидкости равна:

(6)

Высота поднимания (опускания) жидкости уменьшается с повышением температуры, так как при этом α уменьшается быстрее, чем плотность ρ.

Таким образом, зная высоту поднятия жидкости из формулы (5) можно определить значение коэффициента поверхностного натяжения:

(7)

В данной работе смачивание считать полным, R = r радиус кривизны поверхности равен радиусу капилляра, тогда расчетная формула для определения коэффициента поверхностного натяжения имеет вид:

(8)

Капиллярные явления играют большую роль в природе и технике. Капиллярное перемещение жидкости происходит не только в узких трубочках правильной формы, но и любых узких каналах: в щелях, порах, трещинах.

Поступление питательных веществ в корневую систему растения регулируется процессом диффузии, но подъем питательного раствора по стеблю или стволу растения в значительной мере обусловлен явлением капиллярности: раствор поднимается по тонким капиллярным трубкам, образованных стенками растительных клеток.

Пчелы извлекают нектар из глубины цветка посредством очень тонкой капиллярной трубки, находящейся внутри пчелиного хоботка.

По капиллярам почвы вода поднимается из глубинных в поверхностные слои. Уменьшая диаметр почвенных капилляров путем уплотнения почвы, можно усилить приток воды к поверхности почвы, т.е. к зоне испарения и замедлить высыхание почвы. Именно на этом основаны известные агротехнические приемы регулирования водного режима почвы – прикатка и боронование.

Капиллярные явления приходится учитывать в строительном деле, так как многие строительные материалы (песок, известь, бетон), керамические изделия, пористая глина, неглазированный фарфор пронизаны капиллярными ходами, по которым при отсутствии гидроизоляции может проникать влага в помещения.

По капиллярам фитиля поднимается горючие и смазочные вещества (фитильная смазка); на капиллярности основано использование промокательной бумаги и т.п.