Моделирование и идентификация динамических систем
Моделирование линейной динамической системы
Линейная динамическая система задана в виде передаточной функции:
непрерывная система: дискретная система:
| W(p) |
| u (t) |
| y (t) |
| W(z) |
| u (k) |
| y (k) |
· t – непрерывное время,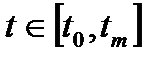 
-заданный интервал времени
· k – номер дискретного момента времени,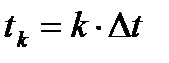 
- дискретный момент времени, 
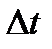- шаг по времени (период дискретизации)
· u (t) – непрерывный, u (k) – дискретный входной сигнал (управление)
· y (t) – непрерывный, y (k) – дискретный выходной сигнал (реакция системы)
· W(p) – передаточная функция в непрерывном и W(z) – дискретном случае
· 
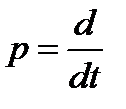– оператор дифференцирования, 
, 
· 
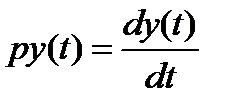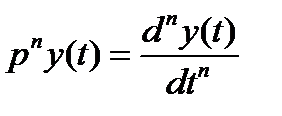
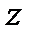- оператор запаздывания (смещения), 
, 
,
, 
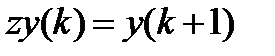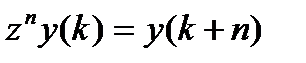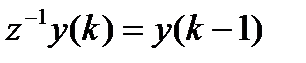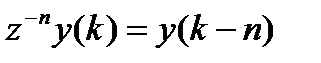
Уравнение непрерывной линейной динамической системы 2-го порядка:
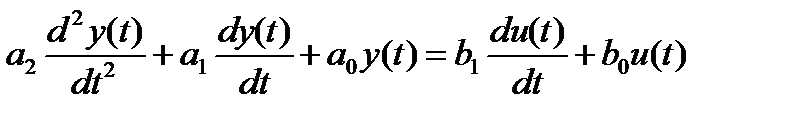
· u (t) – вход системы (управление)
· y (t) – выход системы (реакция)
· 
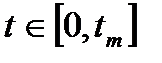– время
Задача моделирования: найти значения выхода системы y (t) на временном диапазоне 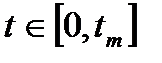при заданных параметрам системы 
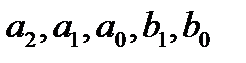и заданном управлении u (t).
Решение задачи моделирования:
Переход к дискретному представлению:
· 
, 
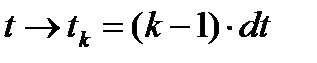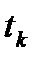- дискретный момент времени, k – номер дискретного момента времени, 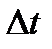- шаг по времени (период дискретизации)
· 
, 
,
· 
, 
· 
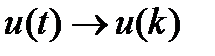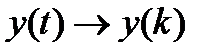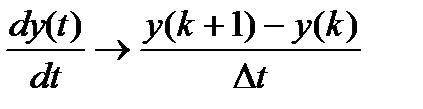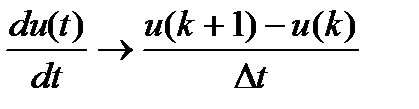
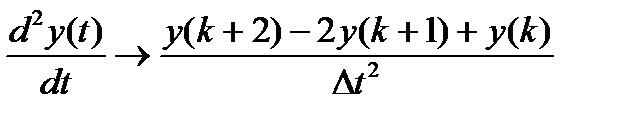
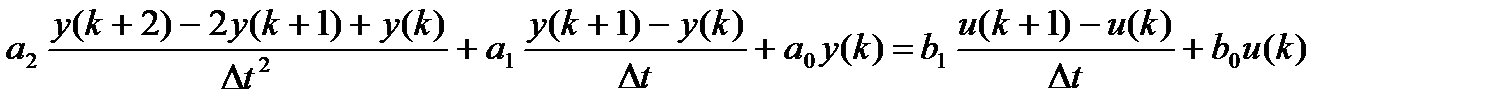
Приводим подобные
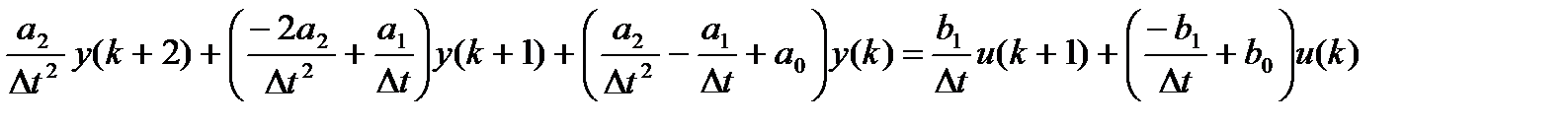
Оставляем в левой части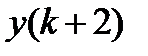 
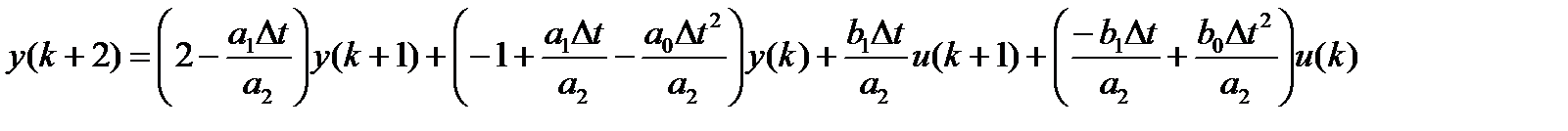
Регрессионное уравнение для моделирования
· 
, 
, 
, 
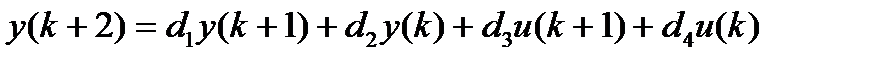
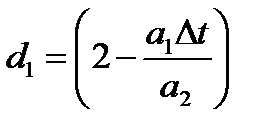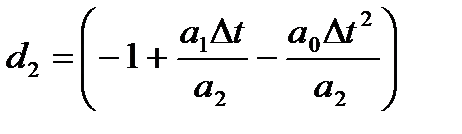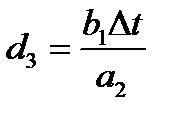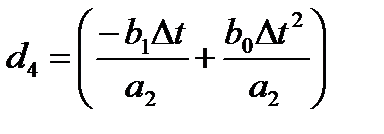
Для моделирования необходимо задать начальные условия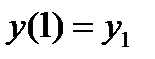 
, 
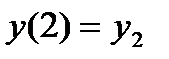- числа.
Аналогично для дискретной системы 2-го порядка
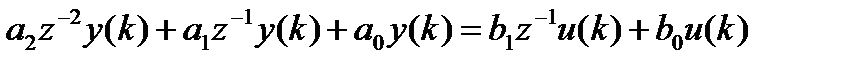
где 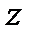- оператор запаздывания (смещения), 
, 
, 
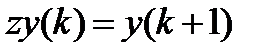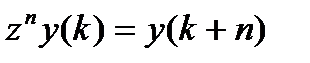
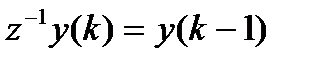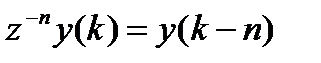, регрессионное уравнение примет вид:
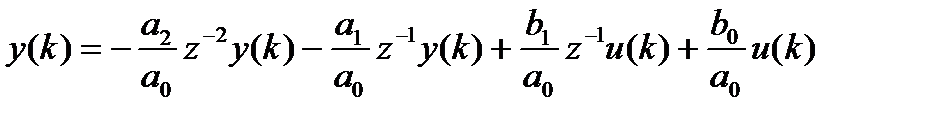
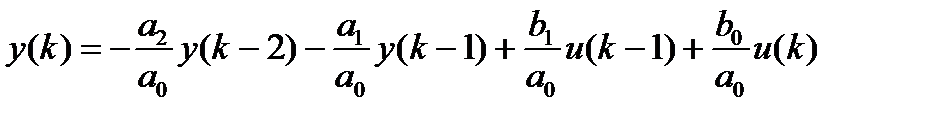
Идентификация линейной динамической системы
Задача идентификации: найти значения выбранных параметров системы (из набора 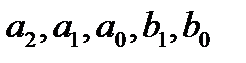) используя данные о входе u (t) и выходе y (t) системы на временном диапазоне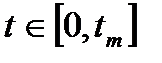
Решение задачи идентификации:
Пример: пусть требуется найти значения параметров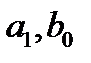 
для непрерывной системы.
Уравнение системы записывается в линейно-регрессионном виде - все слагаемые уравнения содержащие неизвестные параметры записываются в правой части уравнения, все остальное – в левой части:
из 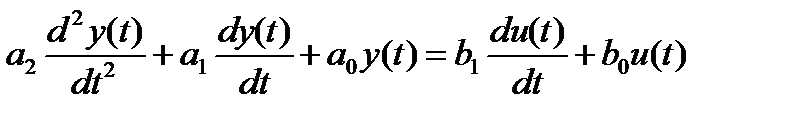получаем:
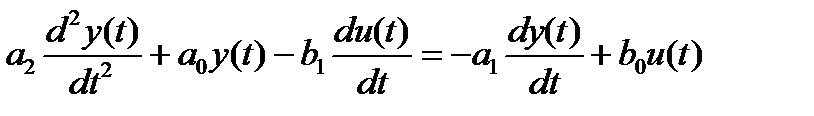
Приводим в дискретный вид:
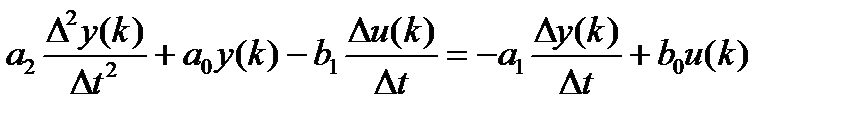
где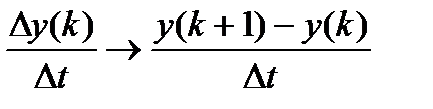 
, 
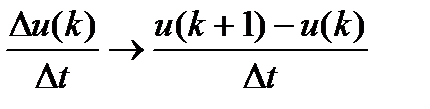
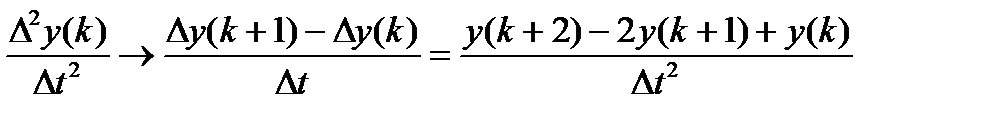
Для расчета дискретной производной 2-го порядка нам потребуется значения функций с запаздыванием на 2 шага. Соответственно выборка данных сократиться на 2 шага и мы будем рассматривать временной диапазон значений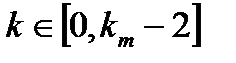 
.
Все что в левой части обозначаем как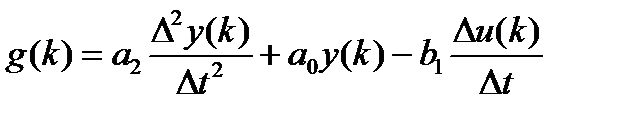 
Правую часть записываем в виде: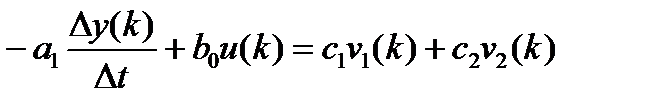 
, где 
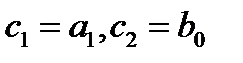- искомые параметры, 
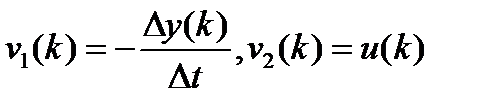- регрессионные переменные (знак относится к переменной а не к параметру).
Получившееся регрессионное уравнение имеет вид
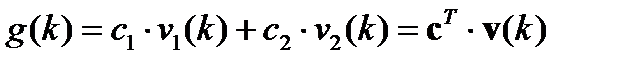
где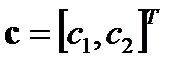 
- вектор параметров, 
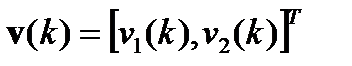- вектор регрессионных переменных.
Схема МНК-идентификации данного регрессионного уравнения имеет вид:
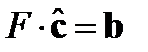
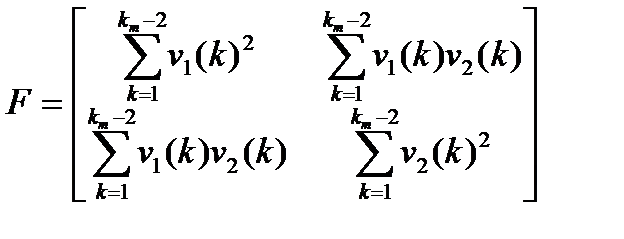
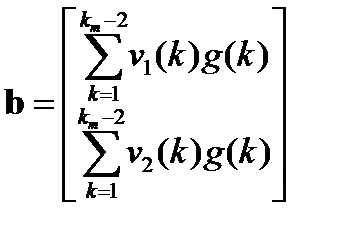
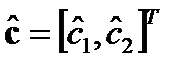- вектор искомых параметров системы.
Решение данной системы записывается в виде:
,
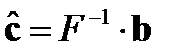где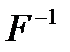 
- обратная матрица к 
.
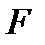Аналогично для дискретной системы 2-го порядка
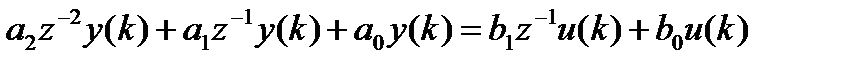
Регрессионное уравнение:
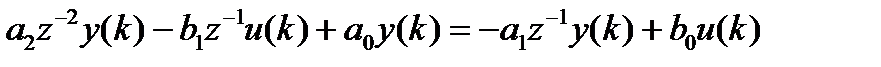
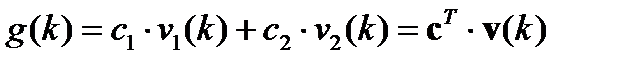
где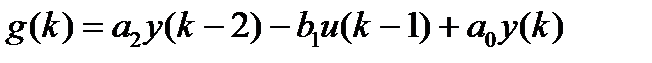 
Правую часть записываем в виде:, где 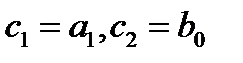- искомые параметры,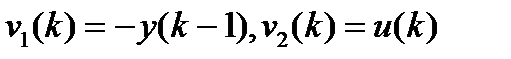 
Задания:
1. Задана передаточная функция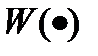 
, период времени 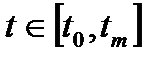, период дискретизации 
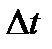и входной сигнал 
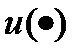(указаны в таблице вариантов заданий). Провести численное моделирование выходного сигнала 
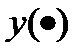и построить график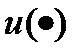и 
и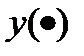 
.
2. По результатам предыдущего задания построить схему МНК-идентификации неизвестных параметров (указаны в таблице вариантов заданий)
Таблица вариантов заданий:
| A | B | |
| 
| |
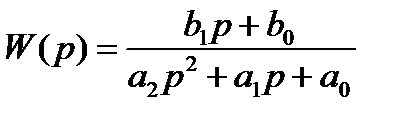
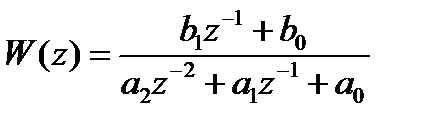
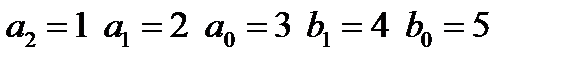входной сигнал: I, 
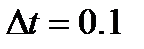неизвестные при идентификации: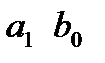 
| 
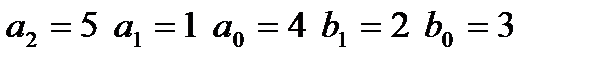входной сигнал: I, 
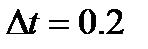неизвестные при идентификации: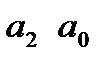 
| |
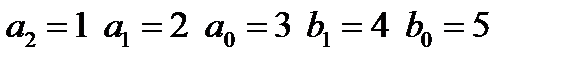входной сигнал: II,
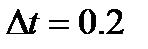неизвестные при идентификации: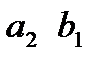 
| 
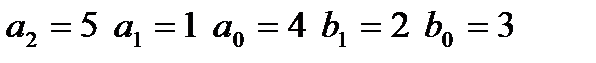входной сигнал: II,
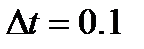неизвестные при идентификации: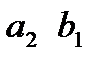
| |
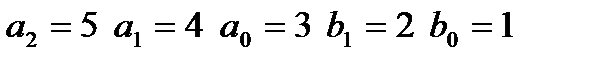входной сигнал: I, 
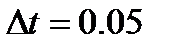неизвестные при идентификации: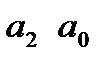
| 
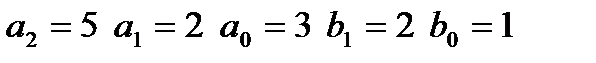входной сигнал: I, 
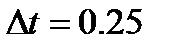неизвестные при идентификации: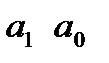 
| |
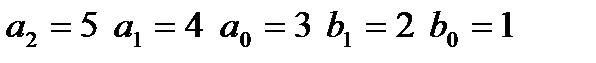входной сигнал: II,
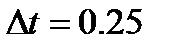неизвестные при идентификации: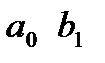 
| 
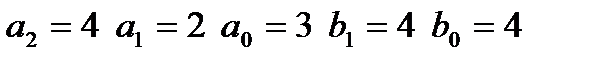входной сигнал: II,
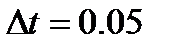неизвестные при идентификации: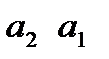 
| |
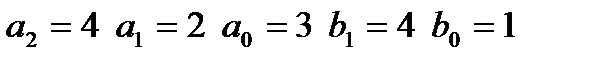входной сигнал: I, 
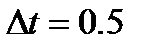неизвестные при идентификации: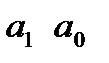
| 
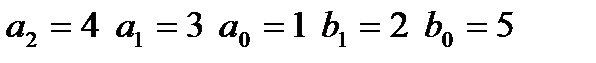входной сигнал: I, 
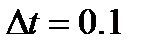неизвестные при идентификации: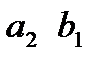
| |
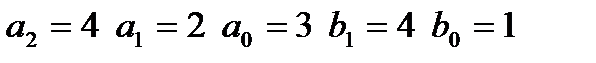входной сигнал: II,
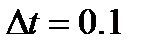неизвестные при идентификации: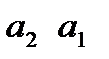
| 
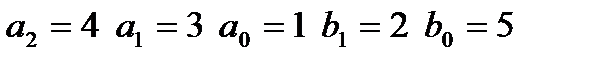входной сигнал: II,
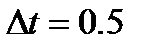неизвестные при идентификации: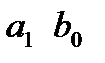
| |
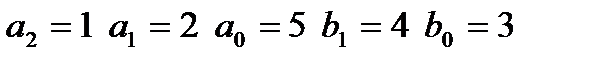входной сигнал: I, 
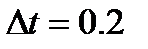неизвестные при идентификации: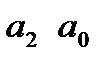
| 
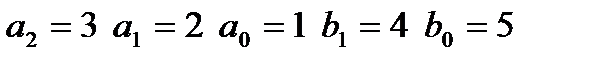входной сигнал: I, 
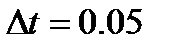неизвестные при идентификации: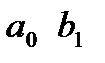
| |
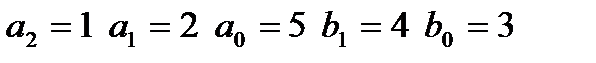входной сигнал: II,
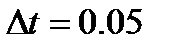неизвестные при идентификации: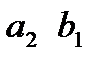
| 
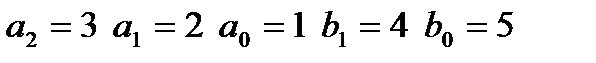входной сигнал: II,
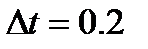неизвестные при идентификации: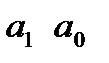
| |
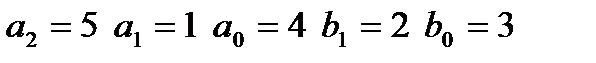входной сигнал: I, 
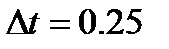неизвестные при идентификации: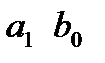
| 
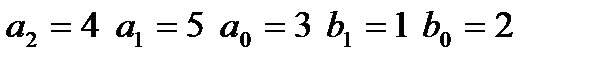входной сигнал: II,
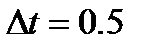неизвестные при идентификации: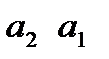
| |
|
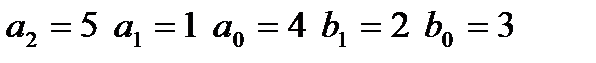входной сигнал: II,
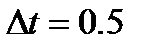неизвестные при идентификации: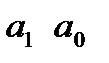
| 
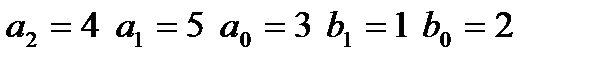входной сигнал: II,
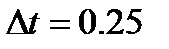неизвестные при идентификации: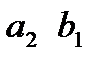
|
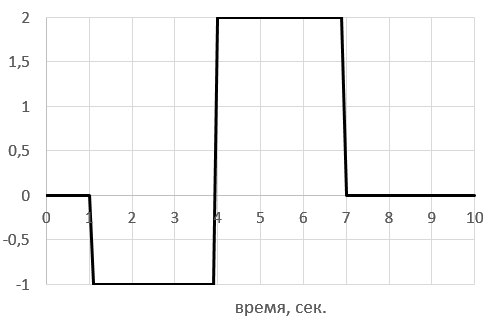
Входные сигналы:
| I | II |
| 
|
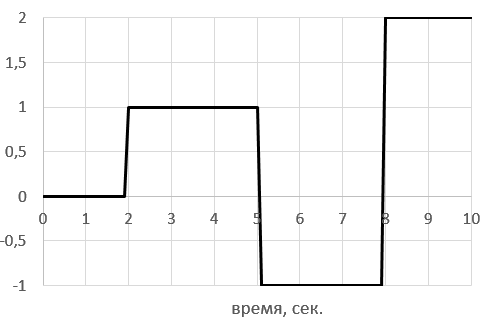