Домашнее задание №4.6-№4.11(в,г)
«Понятие и определение квадратного корня из натурального числа»
Мы довольно долго не знали, что такое корень n-ой степени из действительного числа, и умели обходиться без этого понятия, но потом появились случаи, в которых обойтись без него уже невозможно.
Рассмотрим несколько простейших примеров.
Пример 1: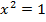 
Решение:
Способ 1, аналитический. Перенесем все члены в левую часть уравнения так, чтобы справа остался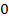 
: 
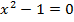. Далее разложим на множители: 
.
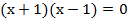Каждый множитель приравниваем к нулю:
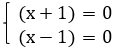
Получаем ответ:
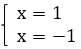
Способ 2, графический. Построим кривую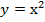 
и прямую 
(рис. 1). Получим 
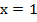и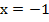 
в точках пересечения графиков.
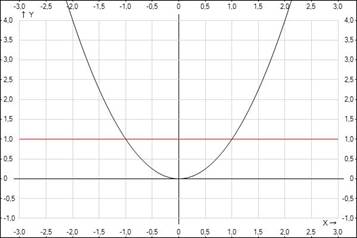
Рис. 1. График уравнений 
и
Ответ. , .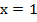
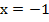Для решения этой задачи нам не потребовалось никаких новых методов.
Пример 2: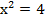 
Решение:
Способ 1.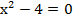 
. Разложим на множители: 
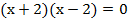. Каждый множитель приравниваем к нулю:
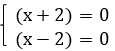
Получаем ответ:
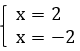
Способ 2, графический. Построим график для системы (рис. 2), где первое уравнение – левая часть заданного выражения (), второе – правая (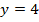
):
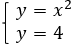
Ответами будут точки пересечения графиков, т. е.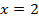 
и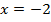 
.
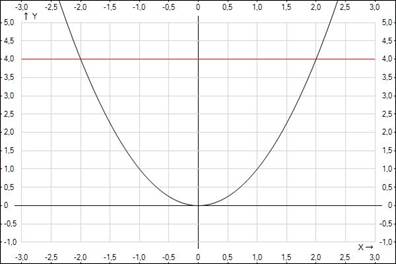
Рис. 2. График уравнени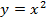й 
и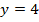
Ответ: , .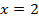
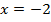После решения двух задач нужды в новом слове не обнаружено.
Пример 3: x2=3
Решение:
Способ 1, аналитический.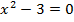 
. Пытаемся разложить на множители, но ничего не выходит. Попробуем другой способ.
Способ 2, графический. Построим график для системы (рис. 3), где первое уравнение – левая часть заданного выражения (), второе – правая (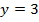
):
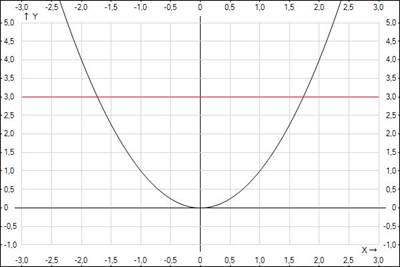
Рис. 3. График уравнений и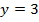
Видим, что графики пересекаются, а значит, ответы все же есть. Назовем их корень квадратный из 3 и минус корень квадратный из 3:
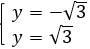
Ответ: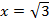 
, 
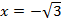
Определение:
Квадратный корень из трех – это иррациональное число, приближенное к десятичной дроби (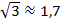
). Так как 
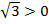, в дальнейшем будем считать его арифметическим корнем.
Теперь нам нужно определить корень n-ой степени из действительного числа.
Рассмотрим еще один пример.
Пример 4: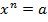 
, где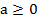 
, 
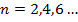
Рис. 4. График функци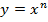й 
и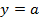 
Уравнение имеет 2 корня: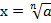 
и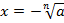 
.
Понятие и определение корня четной степени из неотрицательного числа
Определение:
Корнем n-ой степени из неотрицательного числа а называют такое неотрицательное число, которое при возведении в степень n дает в результате число a.
Т. е. если 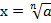, то 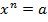. Из этого следует тождество 
.
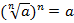Напомним, что у любой функции, в том числе и у данной, есть 2 задачи: прямая (по данному х найти у) и обратная (по данному у, в данном случае равному а, найти х). Если значение а положительное и n четное, то значение у достигается при двух значениях аргумента – положительном и отрицательном. Положительное значение аргумента называется корнем n-ной степени из а, или арифметическим корнем n-ной степени из а.
Перейдем к нечетным степеням. Начнем с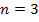 
.
Рис. 5. График функции 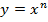, где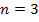
Свойства функции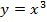 
(рис. 5) отличаются от предыдущих. Напомним, что функция нечетная, график ее симметричен относительно начала координат; она принимает все значения от 
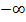до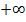 
, а значит, любое свое значение у принимает при единственном значении х. Например, 
; 
; 
; 
; 
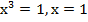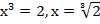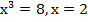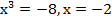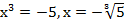. По графику функции (рис. 5) находим решения.
Итак, уравнение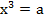 
имеет единственный корень. Если этот корень неотрицательный, он называется арифметическим корнем, в противном случае – минус арифметическим корнем.
Если n – любое нечетное число, график функции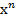 
имеет тот же вид и те же свойства, что и 
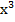: функция нечетная, график симметричен относительно начала координат, область значений от 
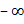до 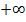, любое значение, в том числе и отрицательное, функция принимает при единственном значении аргумента.