Конспект урока «Возрастание и убывание функции».
Изучение нового материала.
С помощью производной можно находить промежутки монотонности функции. Условимся термин «промежуток» использовать для обозначения таких числовых множеств, как отрезок [a;b], интервал (a;b), полуинтервалы [a;b) и (a;b].
При этом точки a и b называют граничными точками, а все остальные точки интервала (a;b)-внутренними точками промежутка.
Функция f(x) называется возрастающей на некотором промежутке, если большему значению аргумента соответствует большее значение функции, т.е. для любых точек x1 и x2 из этого промежутка, таких, что x2>x1, выполняется неравенство f(x2)>f(x1).
Если для любых точек х1 и х2 данного промежутка, таких, что х2>x1, выполняется неравенство f(x2)<f(x1), то функция f(x) называется убывающей на этом промежутке.
Промежутки возрастания и убывания функции называются промежутками монотонности этой функции.
Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда если f'(x)>0 для всех xϵ(a;b), то функция f(x) возрастает на отрезке [a;b], а если f'(x)<0, то она убывает на этом отрезке.
Применяя определение возрастающей (убывающей) функции трудно найти промежутки монотонности, поэтому мы будем изучать признаки монотонности функции, использующие понятие производной.
Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка, такая cϵ(a;b), что f(b)–f(a)=f'(c)(b–a). f(b)–f(a)=f'(c)(b–a).
Геометрический смысл формулы. Проведем прямую через точки A(a, f(a)) и B(b, f(b)) графика функции y=f(x) и назовем эту прямую секущей. Угловой коэффициент k секущей l равен
Равенство (1) можно записать в виде
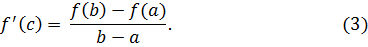
Из равенства (2) и (3) следует, что угловой коэффициент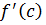 
касательной к графику функции y=f(x) в точке C с абсциссой c равен угловому коэффициенту k секущей l.
Таким образом, на интервале (a;b) найдется такая точка c, что касательная к графику функции y=f(x) в точке C(c; f(c)) параллельна секущей l.
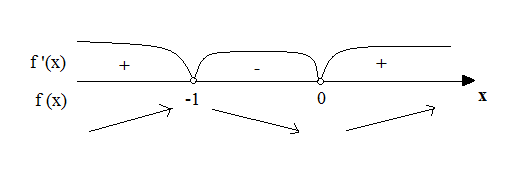
Алгоритм нахождения промежутков возрастания и убывания:
1. Находим производную функции.
2. Находим, при каком значении х, производная функции равна нулю.
3. Находим промежутки, на которые найденная точка разбивает ось Ох, и находим значение производной функции в какой - нибудь точке каждого из интервалов.
4. Находим промежутки возрастания и убывания функции.
ПРИМЕР. Давайте рассмотрим функцию f(x)=2х2+4х-4.
Сначала находим производную этой функции.
f '(x)= (2х2+4х-4)'=4x+4.
Затем производную f'(x) приравниваем к нулю и находим значение х.
f '(x)=0, т.е. 4х+4=0; х=-1.
После этого отмечаем значение х на числовой оси и выясняем какие знаки будут на интервалах.
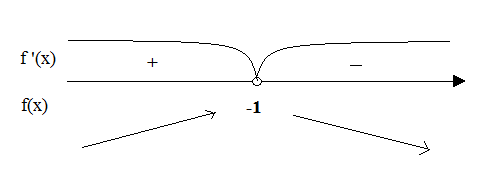
Делаем вывод: т.к. f '(x)>0 на интервале (-∞;-1), то функция f(x) - возрастает;
а на интервале (-1; +∞) функция f(x) -убывает, т.к. f '(x)<0.
Промежутки возрастания и убывания функции называются промежутками монотонности этой функции.
ПРИМЕР: Дана функция f(x)=5x2-3x-1.
Функция сложная, представляет собой сумму нескольких функций, значит найдем производные каждого из слагаемых
f(x)=5x2-3x-1
f '(x)=(5x2-3x-1)'=(5x2)¢-(3x)¢-1¢=10x-3
Найдем, при каком значении х, производная функции равна нулю: f '(x)=0; 10x-3=0; x=0,3.
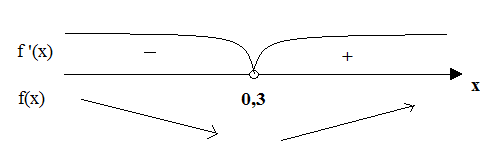
Определяем промежутки возрастания и убывания функции.
Ответ: на интервале (-∞; 0,3) – функция f(x) – убывает, т.к. f '(x)<0;
на интервале (0,3; +∞) – функция возрастает, т.к. f '(x)>0.
